前言
尽管signed语法的使用能带来很多便利,但同时也给表达式的符号确定带来了更多的不确定性。比如一个有符号数和一个无符号数的加法/乘法结果是有符号数还是无符号数?一个有符号数和一个无符号数的比较结果是有符号数还是无符号数?等等。接下来就一起研究下–如何确定一个表达式的正负符号。
一般规则
Verilog规定了计算赋值的步骤如下:
- 根据赋值位长确定原则,确定RHS(表达式右边)的位长
- 如果需要,就扩展RHS。不管LHS(表达式左边)的符号是什么,扩展时都不考虑LHS的符号,只有当RHS是signed,才做符号扩展。
- 赋值时,如果RHS的位长大于LHS的位长,那么直接把多出的位丢弃,以匹配LHS的位长。(有可能把符号位截去)
Verilog语法对于表达式符号位的确定的一般规则:
(1)RHS表达式的符号不依赖于LHS,仅取决于RHS操作数
比如右边是两个有符号数相加,而左边是定义的无符号数,例如:
`timescale 1ns/1ns
module tb_test();
reg signed [3:0] in1,in2;
reg [4:0] out;
initial begin
in1 = 4'b1001; //-7
in2 = 4'b0010; //2
out = in1 + in2; //-5
end
endmodule
仿真结果:

因为结果多出了1位,所以两个加数都会扩展1位,又因为它们都是有符号数,所以高位补符号位,in1从1001到11001,in2从0010到00010,二者相加的结果为:11011。而out是定义的无符号数,所以11011会被解释成 27 ,这就预计的结果 -5 对不上。但-5 的补码又刚好是 11011,说明有符号数之间的运算,其结果也应该定义成有符号数,不然就会出错。
(2)10进制数是有符号数
这里的10进制数是指没有指定位宽和基数的10进制常数,比如1,-12,200等。这很好理解,因为没有指定位宽和基数,肯定只有有符号数才能表示正数和负数。例如:
`timescale 1ns/1ns
module tb_test();
initial begin
$display("-4'd1 = 2'b%b",-1);
end
endmodule
打印结果:
-4’d1 = 2’b11111111111111111111111111111111
可以看出来这肯定是一个有符号数,不然它的值就不是-1了,而是2^32 - 1。
(3)带有基数(base)的数是无符号数(哪怕它没有指定位宽),但是有 s声明的除外。例如:
`timescale 1ns/1ns
module tb_test();
reg [32:0] comp1;
reg [4 :0] comp2,comp3;
//只要看comp的最高位是什么就知道后面的数是有符号数还是无符号数了
initial begin
comp1 = 'd4;
comp2 = 4'd8;
comp3 = 4'sd8;
$display("%b",comp1); //没有指定位宽,但是指定了基数,结果是无符号数
$display("%b",comp2); //指定了位宽和基数,结果是无符号数
$display("%b",comp3); //指定了位宽和基数,同时通过s 指定了它是一个有符号数
end
endmodule
打印结果如下:
000000000000000000000000000000100
01000
11000
comp1、comp2和comp3分别是3个数扩展1位的变量,只要根据它们的首位是0还是1就可以判断这三个数是有符号数还是无符号数(因为结果多了一位,所以会扩充被操作数的符号位,从而可以判断这个数是有符号数还是无符号数)。
(4)位选(bit-select)的结果是无符号数,不管位选操作数是否有符号。域选(part-select)的结果是无符号数,不管域选操作数是否有符号,即使域选的结果是整个向量。
位选就是选中向量的某一位,而域选则是选中向量的某几位。例如:
`timescale 1ns/1ns
module tb_test();
reg signed [3:0] comp; //定义一个有符号数comp
reg [1:0] comp_bit;
reg [3:0] comp_part;
reg [4:0] comp_full;
//只要看comp的最高位是什么就知道后面的数是有符号数还是无符号数了
initial begin
comp = 4'b1001; //-7
comp_bit = comp[3]; //位选中comp的最高位,结果是无符号数
comp_part = comp[3:1]; //域选中comp的高3位,结果是无符号数
comp_full = comp[3:0]; //域选中comp全部,结果是无符号数
$display("%b",comp_bit);
$display("%b",comp_part);
$display("%b",comp_full);
end
endmodule
打印结果如下:
01
0100
01001
从它们的最高位可以看出来都是无符号数。
(5)拼接操作符的结果是无符号的,不管操作数是否有符号,即使是只有一个有符号操作数也是如此。
无论拼接操作是一个或多个有符号数和一个或多个无符号数,它的结果都是无符号数。例如:
`timescale 1ns/1ns
module tb_test();
reg signed [3:0] s_a,s_b; //定义有符号数a,b
reg signed [3:0] us_a,us_b; //定义无符号数a,b
reg [8:0] con1,con2,con3,con4; //拼接结果扩展一位,通过高位判断结果是否有sign
reg [4:0] con5,con6; //拼接结果扩展一位,通过高位判断结果是否有sign
//只要看con的最高位是什么就知道后面的数是有符号数还是无符号数了
initial begin
s_a = 4'b1001;
s_b = 4'b1001;
us_a = 4'b1001;
us_b = 4'b1001;
con1 = {us_a,us_a}; //2个无符号数拼接
con2 = {us_a,s_a}; //1个无符号数和1个有符号数拼接
con3 = {s_a,us_a}; //1个有符号数和1个无符号数拼接
con4 = {s_a,s_a}; //2个有符号数拼接
con5 = {us_a}; //1个无符号数拼接
con6 = {s_a}; //1个有符号数拼接
$display("%b",con1);
$display("%b",con2);
$display("%b",con3);
$display("%b",con4);
$display("%b",con5);
$display("%b",con6);
end
endmodule
打印结果如下:
010011001
010011001
010011001
010011001
01001
01001
从它们的最高位可以看出来都是无符号数。
(6)比较操作符的结果(1、0)是无符号的,不管操作数是否有符号。
因为比较结果其实就是 是 和 否,完全没必要定义成有符号数。例如:
`timescale 1ns/1ns
module tb_test();
reg signed [3:0] s_a,s_b; //定义2个有符号数a,b
reg [1:0] comp; //拼接结果扩展一位,通过高位判断结果是否有sign
//只要看con的最高位是什么就知道后面的数是有符号数还是无符号数了
initial begin
s_a = 4'b1010; //-6
s_b = 4'b1001; //-7
comp = (s_a > s_b); //结果为1的无符号数
$display("%b",comp); //所以高位扩展0,结果是01
end
endmodule
打印结果如下:
01
从它们的最高位可以看出来是无符号数。
(7)如果某操作数是无符号数,则结果是无符号数;只有所有操作数都为有符号数,结果才是有符号数。
但凡运算式中有一个无符号数,那么结果就一定是无符号数,所以最好不要混用有符号数和无符号数。例如:
`timescale 1ns/1ns
module tb_test();
reg signed [3:0] a;
reg signed [4:0] b;
//只要看con的最高位是什么就知道后面的数是有符号数还是无符号数了
initial begin
a = 4'b1010; //-6
b = a + 1'b1; //1'b1是无符号数,导致(a+1'b1)也成了一个有符号数
//$display("%b",pi_int);
end
endmodule
仿真结果:

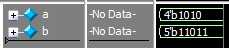
因为表达式中的1’b1是一个无符号数,于是a也被强制转换成了无符号数,然后将其都扩位到5位,等价于5’b01010 + 5’b00001 = 5’b01011,即11。而非预期的(-6+1=-5),即11011。
如果改成这样:
b = a + 1; //1是有符号数,所以(a+1)也是有符号数
那么结果就是11011(即-5),如下所示:
赋值和截断
- 截断(truncation):长位宽数赋值给短位宽数,无论左操作数或右操作数是有符号数还是无符号数,都是直接截断高位。
- 赋值(assignments):短位宽数赋值给长位宽数,需要对高位进行位扩展,具体是扩展1还是扩展0,则依据右操作数而定。如果右操作数是无符号数,则高位扩展0;如果右操作数是有符号数,则高位扩展符号位。
接下来看几个例子,例1:
reg [5:0] a;
reg signed [4:0] b;
initial begin
a = 8'hff; // After the assignment, a = 6'h3f
b = 8'hff; // After the assignment, b = 5'h1f
end
结果:
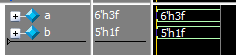
因为a和b的位宽分别是6位和5位,所以要将对应的8’hff的高位截断,结果分别为 a = 6’h3f 和 b = 5’h1f。
例2:
reg [5:0] a;
reg signed [4:0] b, c;
initial begin
a = 8'sh8f; // After the assignment, a = 6'h0f
b = 8'sh8f; // After the assignment, b = 5'h0f
c = -113; // After the assignment, c = 15
end
结果:

因为 8’sh8f 即 8’b1000_1111,截断到a的6位位宽后,所以 a = 6’b00_1111 = 6’h0f;同理,b = 8’sh8f。-113是一个默认的有符号数,位宽为32bit,即32’b1111····10001111,截断到c的4位位宽后,所以 c = 4’b1111 = 15。
例3:
reg [3:0] a;
reg signed [3:0] b;
reg [7:0] c1,c2;
reg signed [7:0] d1,d2;
initial begin
a = 4'b1001;
b = 4'b1001;
c1 = a;
c2 = b;
d1 = a;
d2 = b;
end
结果:
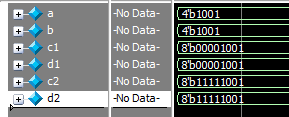
因为c1和d1都是被a赋值的,所以虽然它俩分别是无有符号数和有符号数,但是结果是一样的。因为a是无符号数,所以赋值给8位宽时,需要在高位扩展0,即结果为0000_1001。
因为c2和dd都是被b赋值的,所以虽然它俩分别是无有符号数和有符号数,但是结果是一样的。因为b是有符号数,所以赋值给8位宽时,需要在高位扩展符号位(1),即结果为1111_1001。










![[iOS]使用CocoaPods发布私有库](https://img-blog.csdnimg.cn/direct/5313de0a87484b3081beedb4cc117fb1.png)