对偶问题
- ==**问题一:什么叫做凸二次优化问题?而且为什么符合凸二次优化问题?**==
- 为什么约束条件也是凸的
- 半空间(Half-Space)
- 凸集(Convex Set)
- 半空间是凸集的例子
- SVM 约束定义的半空间
- 总结
- ==**问题二:为什么使用拉格朗日乘子法?原理是什么?**==
- 为什么使用拉格朗日乘子法
- 拉格朗日乘子法的数学原理
- 结合简单例子理解
- 定义问题
- 构建拉格朗日函数
- 对拉格朗日函数求偏导数
- 解方程组并应用KKT条件
- 为何要使 λ ⋅ g ( x ) = 0 \lambda \cdot g(x) = 0 λ⋅g(x)=0
- 经济学角度:
- 数学角度:
- 形象理解:
- 为什么必须满足互补松弛性:
- 求解
- 结论
- ==**问题三:计算偏导的过程**==
- 1. 构建拉格朗日函数
- 2. 对 w w w 和 b b b 求偏导
- 对 \( w \) 求偏导得:
- 对 \( b \) 求偏导得:
- 3. 对 α \alpha α 求偏导
- 总结:
- ==**问题五:带入消去过程是怎样的?**==
- 出发点:拉格朗日函数
- 已知条件:
- 目标:消去 w w w 和 b b b
- 代入 w w w
- 消去 \( b \)
- 得到对偶问题的目标函数
- ==**问题六:SVM中得到KKT条件的过程**==
- KKT条件的推导
问题一:什么叫做凸二次优化问题?而且为什么符合凸二次优化问题?
这个优化问题是凸二次规划问题,因为它具备了凸规划问题所需的两个主要特性:一个凸的目标函数和凸的约束条件。
-
目标函数 1 2 ∣ ∣ ω ∣ ∣ 2 \frac{1}{2} ||\omega||^2 21∣∣ω∣∣2 是凸的:因为这个函数的二阶导数相对于 ω \omega ω 为正值,这保证了该函数是凸的,也就是说,它在任意方向上都是
向上的弓形。 -
约束条件是凸的:对于 SVM 的约束 y i ( ω T x i + b ) ≥ 1 y_i(\omega^T x_i + b) \geq 1 yi(ωTxi+b)≥1,它们定义了一个
凸集。
为什么约束条件也是凸的
为了形成凸优化问题,约束条件本身也必须形成一个凸集。在 SVM 的情况下,这些约束定义了数据点应位于由 超平面定义的决策边界的一侧 。具体来说,对于标签为 +1 的数据点,它们位于超平面 ω T x i + b = 0 \omega^T x_i + b = 0 ωTxi+b=0 的一侧;对于标签为 -1 的数据点,它们位于另一侧。这意味着超平面两侧的空间是半空间,而半空间的性质是凸的。
半空间(Half-Space)
在几何中,半空间是指通过空间中一个点的平面(在二维空间中是一条线)所划分的空间的任意一侧。例如,对于二维空间中的直线 ( ax + by + c = 0 ),半空间可以是这条线的上方或下方区域,即所有满足 ( ax + by + c > 0 ) 或 ( ax + by + c < 0 ) 的点的集合。
在 SVM 的上下文中,我们在高维空间中处理数据点,而超平面 ω T x + b = 0 \omega^T x + b = 0 ωTx+b=0 划分了这个高维空间。超平面的一侧是由所有满足 ω T x + b > 0 \omega^T x + b > 0 ωTx+b>0 的点组成的半空间,另一侧是由所有满足 ω T x + b < 0 \omega^T x + b < 0 ωTx+b<0 的点组成的半空间。
凸集(Convex Set)
一个集合是凸的,如果集合中任意两点之间的连线上的点也属于这个集合。更正式地说,如果对于集合中的任意两点
x
1
x_1
x1 和
x
2
x_2
x2,以及对于所有
λ
\lambda
λ 满足
0
≤
λ
≤
1
0 \leq \lambda \leq 1
0≤λ≤1,下面的关系成立:
λ
x
1
+
(
1
−
λ
)
x
2
也在集合中
\lambda x_1 + (1 - \lambda) x_2 \text{ 也在集合中}
λx1+(1−λ)x2 也在集合中
这就意味着你不能在两点之间画一条线段,然后找到线段上的一个点,它不在集合中。
半空间是凸集的例子
半空间是凸集的典型例子 ,因为如果你取半空间中的任意两点,由于这两点都满足超平面的同侧不等式(比如
ω
T
x
+
b
>
0
\omega^T x + b > 0
ωTx+b>0),它们之间的任何线性组合也必然满足同样的不等式,因此也在这个半空间内。这个性质保证了半空间的连线始终保持在半空间内部,满足凸集的定义。
SVM 约束定义的半空间
在 SVM 中,每个数据点
x
i
x_i
xi 的约束
y
i
(
ω
T
x
i
+
b
)
≥
1
y_i(\omega^T x_i + b) \geq 1
yi(ωTxi+b)≥1 实际上定义了一个半空间,其中包含了所有与该数据点 同侧的点 。由于所有的数据点都满足它们各自的约束(对于正类是超平面的一侧,对于负类是另一侧),所以当我们考虑所有这些约束时,我们得到的是这些半空间的交集。这个交集自然也是凸的,因为它是凸集(各个半空间)的交集。
总结
所以,当我们说 SVM 的优化问题是凸二次规划问题时,我们是基于两个观察:
- 目标函数是凸的二次函数。
- 每个约束条件单独定义了一个半空间,整个约束集合(所有数据点的约束的交集)形成了一个凸集。
这两点共同确保了整个优化问题是凸的,它有一个唯一的全局最优解,而且可以使用有效的优化算法找到这个解。凸优化问题在数学和工程上都是极为重要的,因为它们通常可以通过已知的算法高效且准确地求解。
问题二:为什么使用拉格朗日乘子法?原理是什么?
这个SVM的原始定义是符合凸二次优化的,所以说可以使用现成的优化计算,但是我们可以使用更高效的方法。
是因为它本身就是凸二次优化问题吗?而且为什么要得到这个“对偶问题”?对偶问题是什么?怎么就突然提出使用拉格朗日乘子了?
拉格朗日乘子法是解决带约束优化问题的一种方法。当你的优化问题包含一些约束条件时,直接对目标函数进行优化可能会很复杂或者不可行,因为你需要在满足所有约束的同时寻找最优解。拉格朗日乘子法通过引入额外的变量(称为 拉格朗日乘子 )将约束条件融合进目标函数中,从而转化成一个无约束优化问题。
为什么使用拉格朗日乘子法
-
引入拉格朗日乘子法的动机:在某些情况下,我们面对的优化问题不仅仅是找到最小或最大值,还要在某些条件或约束下找到这些极值。这些条件通常以等式或不等式的形式给出。如果试图直接解决这样的问题,我们可能会发现
很难直接应用标准的优化技术,因为不是在全空间中寻找极值,而是在一个受限的区域内。拉格朗日乘子法提供了一种机制,可以将约束条件 集成到目标函数中 ,这使得问题可以在不直接考虑这些约束的情况下被解决。 -
如何实现无约束优化:拉格朗日乘子法通过为
每个约束引入一个额外的变量(拉格朗日乘子)来工作。对于每个约束条件,乘子将其与目标函数 相乘并加 起来,构建一个新的函数(拉格朗日函数)。在拉格朗日函数中,如果约束条件被违反,乘子将罚分(惩罚项)添加到目标函数中,使得该函数值增加 。如果约束被满足,乘子的作用被“关闭”,不会影响 目标函数的值。
拉格朗日乘子法的数学原理
-
构建拉格朗日函数:考虑一个简化的例子,有一个目标函数 f ( x ) f(x) f(x) 需要
最小化,同时要满足一个约束 g ( x ) = 0 g(x) = 0 g(x)=0。拉格朗日函数 L ( x , λ ) = f ( x ) + λ g ( x ) L(x, \lambda) = f(x) + \lambda g(x) L(x,λ)=f(x)+λg(x) 被构造出来,其中 λ \lambda λ 是拉格朗日乘子。 -
最优解的条件:当 L ( x , λ ) L(x, \lambda) L(x,λ) 对 ( x ) 和 λ \lambda λ 的导数同时为零时,这表明我们找到了原始问题的候选解。这里的关键是,通过调整 λ \lambda λ ,可以“开启”或“关闭”对 f ( x ) f(x) f(x) 的罚分,从而确保在最优解 ( x ) 处约束 g ( x ) = 0 g(x) = 0 g(x)=0 被满足。
-
对偶性:拉格朗日乘子法引出了原问题的
对偶问题。对偶问题通常更容易求解 ,因为它最大化了关于拉格朗日乘子的最小化问题。在某些情况下,原问题和对偶问题有相同的解,这是通过所谓的 对偶性原理 来证明的。 -
优势:拉格朗日乘子法特别适用于约束是
线性的情况,这时约束条件对应的几何图形是平面或直线。这个方法也能很自然地拓展到不等式约束,这是通过所谓的 KKT(Karush-Kuhn-Tucker)条件来实现的,它是拉格朗日乘子法在不等式约束下的推广。
结合简单例子理解
考虑一个非常简单的优化问题:
假设目标函数是 f ( x ) = x 2 f(x) = x^2 f(x)=x2,我们需要找到 ( x ) 的值来最小化这个函数,但现在有一个不等式约束 g ( x ) = x − 2 ≥ 0 g(x) = x - 2 \geq 0 g(x)=x−2≥0,也就是 ( x ) 必须大于等于 2。
定义问题
- 目标函数: f ( x ) = x 2 f(x) = x^2 f(x)=x2
- 约束条件: g ( x ) = x − 2 ≥ 0 g(x) = x - 2 \geq 0 g(x)=x−2≥0
构建拉格朗日函数
在有约束的优化问题中,我们构造拉格朗日函数 L ( x , λ ) L(x, \lambda) L(x,λ) 是为了将约束条件融入到目标函数中,从而可以使用无约束优化的方法来求解。拉格朗日函数是这样定义的:
L
(
x
,
λ
)
=
f
(
x
)
+
λ
⋅
g
(
x
)
L(x, \lambda) = f(x) + \lambda \cdot g(x)
L(x,λ)=f(x)+λ⋅g(x)
其中,
f
(
x
)
f(x)
f(x) 是我们希望最小化的原始目标函数,
g
(
x
)
g(x)
g(x) 是约束函数,
λ
\lambda
λ 是拉格朗日乘子。
因此,我们的拉格朗日函数是:
L ( x , λ ) = f ( x ) + λ ⋅ g ( x ) = x 2 + λ ⋅ ( x − 2 ) L(x, \lambda) = f(x) + \lambda \cdot g(x) = x^2 + \lambda \cdot (x - 2) L(x,λ)=f(x)+λ⋅g(x)=x2+λ⋅(x−2)
对拉格朗日函数求偏导数
-
对 ( x ) 求偏导得到:
∂ L ∂ x = 2 x + λ \frac{\partial L}{\partial x} = 2x + \lambda ∂x∂L=2x+λ -
对 λ \lambda λ 求偏导得到:
∂ L ∂ λ = x − 2 \frac{\partial L}{\partial \lambda} = x - 2 ∂λ∂L=x−2
解方程组并应用KKT条件
KKT条件是在带约束的优化问题中,特别是当约束为不等式时,用来找到 最优解的必要条件 。这些条件是由Karush于1939年和Kuhn与Tucker于1951年提出的。它们是拉格朗日乘子法在不等式约束下的一种推广。让我们来详细解释每个条件的意义和原因:
-
原始问题的约束必须满足:这意味着任何可行的解必须遵守问题中给出的所有约束。如果约束是 g ( x ) ≥ 0 g(x) \geq 0 g(x)≥0 ,那么任何解都不能使 g ( x ) g(x) g(x) 变为负值,因为那将违反问题的规定。
-
拉格朗日乘子必须非负:在带有不等式约束 g ( x ) ≥ 0 g(x) \geq 0 g(x)≥0 的情况下,如果我们允许 λ \lambda λ 成为负值,这实际上会
“鼓励”违反约束,因为负值的 λ \lambda λ 会减少拉格朗日函数的值,即使 g ( x ) g(x) g(x) 是正的。因此,要保持优化问题的完整性和约束的作用, λ \lambda λ 必须是非负的。 -
互补松弛性:这个条件描述了最优解时拉格朗日乘子和约束函数之间的关系。互补松弛性的意思是,对于最优解,如果 λ > 0 \lambda > 0 λ>0,那么相应的约束函数 g ( x ) g(x) g(x) 必须为零(即约束在最优解处是“活跃”的或“紧的”),反之亦然。对于每个拉格朗日乘子 λ \lambda λ,它要么是0,要么对应的约束函数 g ( x ) g(x) g(x) 的值为0(即 λ ⋅ g ( x ) = 0 \lambda \cdot g(x) = 0 λ⋅g(x)=0)
为何要使 λ ⋅ g ( x ) = 0 \lambda \cdot g(x) = 0 λ⋅g(x)=0
拉格朗日乘子法的关键在于,我们希望能够调整
λ
\lambda
λ 和 (x) 的值,使得
L
(
x
,
λ
)
L(x, \lambda)
L(x,λ) 的值最小化,同时不违反任何约束。这里有两个主要目的:
-
最小化目标函数 f ( x ) f(x) f(x):我们希望找到使 f ( x ) f(x) f(x)达到最小的(x)值。
-
满足约束 g ( x ) ≥ 0 g(x) \geq 0 g(x)≥0:约束必须被满足。互补松弛性( λ ⋅ g ( x ) = 0 \lambda \cdot g(x) = 0 λ⋅g(x)=0)确保了这一点:
- 如果 g ( x ) > 0 g(x) > 0 g(x)>0(即约束“过度”满足),那么 λ \lambda λ 应为0,以避免 λ ⋅ g ( x ) \lambda \cdot g(x) λ⋅g(x) 对 L ( x , λ ) L(x, \lambda) L(x,λ) 造成任何影响,因为约束 已经被满足,不需要通过 λ \lambda λ 来“激活”或强化这一约束。
- 如果
g
(
x
)
=
0
g(x) = 0
g(x)=0(即约束恰好满足),
λ
\lambda
λ 可以是任何
非负值,因为此时拉格朗日乘子 λ \lambda λ 起到确保我们正好处于约束边界的作用,此时 λ \lambda λ的值将反映出维持这个约束的重要性。
这确保了在最优解处,任何非零的拉格朗日乘子都
恰好对应于一个正好被满足的约束,这意味着这些约束正好界定了解的空间,而不是被过分限制或根本不起作用。
互补松弛性是KKT条件中的一个关键部分,它确保了在最优解处约束要么是活跃的,要么对应的拉格朗日乘子是0。互补松弛性的原理可以从经济学角度和数学角度进行理解:经济学角度:
想象拉格朗日乘子 λ \lambda λ 是对资源的价格或者价值的衡量。如果一个资源(对应于一个约束)是 多余 的,那么它的“价格” λ \lambda λ 将会是0,因为市场上已经有足够的资源了,不需要额外支付成本。反之,如果资源是稀缺的(约束是紧的,也就是 约束恰好在等式上 ),那么这个资源的价格 λ \lambda λ 必须大于0。
数学角度:
当我们用拉格朗日乘子法解决约束优化问题时,我们实际上是在寻找一个点,这个点不仅使目标函数 f ( x ) f(x) f(x) 达到 最小值 ,而且还要满足所有给定的
约束g ( x ) ≥ 0 g(x) \geq 0 g(x)≥0。拉格朗日函数 L ( x , λ ) L(x, \lambda) L(x,λ) 的形式如下:
L ( x , λ ) = f ( x ) + λ ⋅ g ( x ) L(x, \lambda) = f(x) + \lambda \cdot g(x) L(x,λ)=f(x)+λ⋅g(x)
我们通过对 (L) 关于 (x) 和 λ \lambda λ 分别求偏导并设置为零来寻找最优点【函数最小值】:
∂ L ∂ x = 0 和 ∂ L ∂ λ = 0 \frac{\partial L}{\partial x} = 0 \quad \text{和} \quad \frac{\partial L}{\partial \lambda} = 0 ∂x∂L=0和∂λ∂L=0
- 当 g ( x ) = 0 g(x) = 0 g(x)=0(约束在最优解处是
活跃的):- λ \lambda λ 可能不为零,因为它帮助在保持 g ( x ) = 0 g(x) = 0 g(x)=0 的同时使 L L L 达到
最小值。- 当 g ( x ) > 0 g(x) > 0 g(x)>0(约束在最优解处是
非活跃的):- 由于 g ( x ) g(x) g(x) 已经是正值,所以增加 (x) 使 g ( x ) g(x) g(x) 增加(即 越来越满足约束)不会改变 f ( x ) f(x) f(x) 的值。因此,为了使 L ( x , λ ) L(x, \lambda) L(x,λ) 的
导数为零, λ \lambda λ 必须是0。因为如果 λ \lambda λ 不是0, λ ⋅ g ( x ) \lambda \cdot g(x) λ⋅g(x) 将会增加 (L) 的值,这与最小化 (L) 目标相违背。形象理解:
可以这样理解互补松弛性:它就像是一种平衡状态,其中拉格朗日乘子 λ \lambda λ 和约束 g ( x ) g(x) g(x) 之间的关系必须是互相抵消的。如果约束未被满足 g ( x ) g(x) g(x) 是活跃的),那么乘子 λ \lambda λ 需要“打开”来应用惩罚,反之,如果约束是非活跃的 g ( x ) g(x) g(x) 不是紧的),那么没有必要应用惩罚,因此乘子 λ \lambda λ 为0。
为什么必须满足互补松弛性:
如果不满足互补松弛性,我们可能会得到一个不正确的最优解。例如,如果 λ > 0 \lambda > 0 λ>0 但 g ( x ) > 0 g(x) > 0 g(x)>0 ,这意味着
约束不是限制因素,但我们仍然在目标函数中应用了一个正的乘子,从而错误地增加了目标函数的值。这会导致我们找到一个不实际满足所有约束的解。
互补松弛性确保了我们只在必要时才对目标函数施加约束的影响,从而获得真正满足所有约束的最优解。在实际操作中,互补松弛性可以用来检验一个潜在解是否真正是最优解,也是在数值优化算法中检查解的可行性和优化性的一个标准。
根据互补松弛性,如果 x > 2 x > 2 x>2,那么 λ \lambda λ 必须为0;如果 x = 2 x = 2 x=2,那么 λ \lambda λ 可以为任何非负数。
求解
由于 ∂ L ∂ λ = x − 2 \frac{\partial L}{\partial \lambda} = x - 2 ∂λ∂L=x−2,互补松弛性意味着 λ \lambda λ 只能在 ( x = 2 ) 时非零。这给我们以下情况:
- 如果 ( x > 2 ),那么 λ = 0 \lambda = 0 λ=0。此时 ∂ L ∂ x = 2 x \frac{\partial L}{\partial x} = 2x ∂x∂L=2x,最小化 f ( x ) f(x) f(x) 的解是 ( x ) 趋于无穷小。
- 如果 ( x = 2 ),这满足约束 g ( x ) ≥ 0 g(x) \geq 0 g(x)≥0,且 λ \lambda λ 可以为任意非负数,最小化 f ( x ) f(x) f(x) 的解是 ( x = 2 )。
结论
在这个特定的例子中,最小化 x 2 x^2 x2 的解是 ( x = 2 ),这是约束 x ≥ 2 x \geq 2 x≥2 允许的最小值。换句话说,在约束 g ( x ) g(x) g(x) 的作用下,目标函数 f ( x ) f(x) f(x) 在 x = 2 x = 2 x=2 时达到最小。这也与直观感觉一致,因为 f ( x ) f(x) f(x) 是一个开口向上的抛物线,它在 x = 0 x = 0 x=0 时最小,但由于 ( x ) 必须大于等于2,所以在满足约束的最小 ( x ) 值上达到最小。
问题三:计算偏导的过程

这里是求导的过程是什么?
这张图片展示了SVM优化问题的对偶形式和通过拉格朗日乘子法得到的一些关键方程。求导过程是这样的:
1. 构建拉格朗日函数
拉格朗日函数 ( L(w, b, \alpha) ) 在这里是优化问题的对偶形式,表达式为:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) L(w, b, \alpha) = \frac{1}{2} \|w\|^2 + \sum_{i=1}^{m} \alpha_i (1 - y_i(w^T x_i + b)) L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(wTxi+b))
其中:
- ∥ w ∥ 2 \|w\|^2 ∥w∥2 是权重向量的平方范数(也就是向量元素的平方和)。
- ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) \sum_{i=1}^{m} \alpha_i (1 - y_i(w^T x_i + b)) ∑i=1mαi(1−yi(wTxi+b)) 是拉格朗日乘子与约束条件的乘积和。
问题四:为什么是 1 − y i ( w T x i + b ) 1 - y_i(w^T x_i + b) 1−yi(wTxi+b)而不是$ y_i(w^T x_i + b) - 1$呢?
当我们将这个条件表示为一个优化问题时,我们会想要最小化目标函数的同时,满足所有的约束条件。在这个上下文中, 1 − y i ( w T x i + b ) 1 - y_i(w^T x_i + b) 1−yi(wTxi+b)实际上是一个方便的数学表达,用于在拉格朗日优化框架下表示约束条件。
对于正类样本,我们希望 w T x i + b ≥ 1 w^T x_i + b \geq 1 wTxi+b≥1,这可以重写为 1 − ( w T x i + b ) ≤ 0 1 - (w^T x_i + b) \leq 0 1−(wTxi+b)≤0。
对于负类样本,我们希望 w T x i + b ≤ − 1 w^T x_i + b \leq -1 wTxi+b≤−1,这可以重写为 1 − ( − w T x i − b ) ≤ 0 1 - (-w^T x_i - b) \leq 0 1−(−wTxi−b)≤0,这与正类样本的约束形式是一致的。
所以,当我们把所有的样本(无论正类或负类)都使用同一形式的约束 1 − y i ( w T x i + b ) ≤ 0 1 - y_i(w^T x_i + b) \leq 0 1−yi(wTxi+b)≤0 来表示时,就可以简化数学表达,并且统一处理所有样本对于决策边界的约束。
总结一下:
- y i = + 1 y_i = +1 yi=+1 的情况下, 1 − y i ( w T x i + b ) 1 - y_i(w^T x_i + b) 1−yi(wTxi+b) 等同于 1 − ( w T x i + b ) ≤ 0 1 - (w^T x_i + b) \leq 0 1−(wTxi+b)≤0,这反映了 w T x i + b ≥ 1 w^T x_i + b \geq 1 wTxi+b≥1。
- y i = − 1 y_i = -1 yi=−1 的情况下, 1 − y i ( w T x i + b ) 1 - y_i(w^T x_i + b) 1−yi(wTxi+b) 等同于 1 + w T x i + b ≤ 0 1 + w^T x_i + b \leq 0 1+wTxi+b≤0,这反映了 w T x i + b ≤ − 1 w^T x_i + b \leq -1 wTxi+b≤−1。
2. 对 w w w 和 b b b 求偏导
为了最小化 L ( w , b , α ) L(w, b, \alpha) L(w,b,α),需要对 w w w 和 b b b 分别求偏导并令其为零。
对 ( w ) 求偏导得:
∂ L ∂ w = w − ∑ i = 1 m α i y i x i \frac{\partial L}{\partial w} = w - \sum_{i=1}^{m} \alpha_i y_i x_i ∂w∂L=w−i=1∑mαiyixi
令偏导数为零得到 ( w ) 的最优解:
w
−
∑
i
=
1
m
α
i
y
i
x
i
=
0
w - \sum_{i=1}^{m} \alpha_i y_i x_i = 0
w−i=1∑mαiyixi=0
w = ∑ i = 1 m α i y i x i w = \sum_{i=1}^{m} \alpha_i y_i x_i w=i=1∑mαiyixi
对 ( b ) 求偏导得:
∂ L ∂ b = − ∑ i = 1 m α i y i \frac{\partial L}{\partial b} = -\sum_{i=1}^{m} \alpha_i y_i ∂b∂L=−i=1∑mαiyi
同样,令偏导数为零得到 ( b ) 的条件:
−
∑
i
=
1
m
α
i
y
i
=
0
-\sum_{i=1}^{m} \alpha_i y_i = 0
−i=1∑mαiyi=0
∑
i
=
1
m
α
i
y
i
=
0
\sum_{i=1}^{m} \alpha_i y_i = 0
i=1∑mαiyi=0
这是因为偏导数等于 − ∑ α i y i -\sum \alpha_i y_i −∑αiyi,并且没有 b b b 直接作为一个项出现在 L L L 中。
3. 对 α \alpha α 求偏导
对 α \alpha α 的偏导数不是显式地求解,而是通过上述条件和原始问题中的约束来求解 α \alpha α。在这个过程中,我们必须保证所有的 α i ≥ 0 \alpha_i \geq 0 αi≥0。
总结:
- 等式 w = ∑ i = 1 m α i y i x i w = \sum_{i=1}^{m} \alpha_i y_i x_i w=∑i=1mαiyixi 显示了如何通过拉格朗日乘子 α \alpha α 表达权重向量 w w w。
- 等式 ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 ∑i=1mαiyi=0 提供了一个关于 b b b 的条件,即所有 α \alpha α 与对应的 y y y 的乘积之和必须为0。
这两个条件一起,描述了如何在对偶问题中找到 ( w ) 和 ( b ) 的最优值,这些值满足原始SVM问题的优化条件。这个过程中的数学推导和分析是为了确保在满足所有约束的同时,能找到最小化原始问题的最优解。
问题五:带入消去过程是怎样的?

出发点:拉格朗日函数
原始的拉格朗日函数
L
(
w
,
b
,
α
)
L(w, b, \alpha)
L(w,b,α) 是:
L
(
w
,
b
,
α
)
=
1
2
∥
w
∥
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
)
L(w, b, \alpha) = \frac{1}{2} \|w\|^2 + \sum_{i=1}^{m} \alpha_i (1 - y_i(w^T x_i + b))
L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(wTxi+b))
已知条件:
根据KKT条件,我们有两个重要的关系:
- w = ∑ i = 1 m α i y i x i w = \sum_{i=1}^{m} \alpha_i y_i x_i w=∑i=1mαiyixi(等式 6.9)
- ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 ∑i=1mαiyi=0(等式 6.10)
目标:消去 w w w 和 b b b
我们希望在不涉及 w w w 和 b b b 的情况下重写 L L L。首先用 w w w 的表达式来替换原始 L L L 中的 w w w
代入 w w w
将
w
w
w 的表达式代入
∥
w
∥
2
\|w\|^2
∥w∥2:
∥
w
∥
2
=
(
∑
i
=
1
m
α
i
y
i
x
i
)
T
(
∑
j
=
1
m
α
j
y
j
x
j
)
=
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
\|w\|^2 = \left( \sum_{i=1}^{m} \alpha_i y_i x_i \right)^T \left( \sum_{j=1}^{m} \alpha_j y_j x_j \right) = \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^T x_j
∥w∥2=(i=1∑mαiyixi)T(j=1∑mαjyjxj)=i=1∑mj=1∑mαiαjyiyjxiTxj
在SVM的对偶形式中,我们首先定义了权重向量 w w w 作为拉格朗日乘子 α \alpha α 的函数:
w = ∑ i = 1 m α i y i x i w = \sum_{i=1}^{m} \alpha_i y_i x_i w=i=1∑mαiyixi
由于 w w w 是一个向量,我们可以通过将它与自身的转置相乘来计算它的平方范数,这实际上是在计算 w w w 的每个分量的平方和。所以,我们的计算步骤是这样的:
-
考虑 (w) 的定义:
- w w w 是通过对每个支持向量 x i x_i xi 与对应的拉格朗日乘子 α i \alpha_i αi 和类别标签 y i y_i yi 的乘积求和来得到的。
-
计算 w w w 的平方范数 ( ∥ w ∥ 2 \|w\|^2 ∥w∥2):
- 要计算向量的平方范数,我们将该向量与其
转置相乘。 - 在线性代数中,当你计算一个向量与其转置的乘积时,你实际上是在计算该向量每个分量的平方和。
- 要计算向量的平方范数,我们将该向量与其
-
进行代数展开:
- 展开 w w w 的表达式,我们将 α i y i x i \alpha_i y_i x_i αiyixi 与 a l p h a j y j x j alpha_j y_j x_j alphajyjxj 相乘。
- 注意,我们使用了两个不同的索引 (i) 和 (j) 来表示乘法中的两个不同的项。当我们展开双重求和时,我们对所有可能的 (i) 和 (j) 组合进行求和。这样,每一对 (i, j) 都会有一个对应的项。
-
理解乘法中的双重索引:
- 双重索引 (i) 和 (j) 允许我们考虑
w
w
w 中所有不同的项之间的
所有可能乘积。 - 当 (i) 等于 (j) 时,我们计算的是
x
i
x_i
xi 自己与自己的
点积,也就是它自己的平方。 - 当 (i) 不等于 (j) 时,我们计算的是两个
不同支持向量之间的点积。
- 双重索引 (i) 和 (j) 允许我们考虑
w
w
w 中所有不同的项之间的
消去 ( b )
由于 ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 ∑i=1mαiyi=0,拉格朗日函数中任何包含 ( b ) 的项乘以这个和都将为0,所以这些项可以省略。
得到对偶问题的目标函数
现在我们可以重写 ( L ),省略 ( b ) 并使用 ( w ) 的新表达式:
L
(
α
)
=
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
+
∑
i
=
1
m
α
i
−
∑
i
=
1
m
α
i
y
i
(
∑
j
=
1
m
α
j
y
j
x
j
T
)
x
i
−
b
∑
i
=
1
m
α
i
y
i
L(\alpha) = \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum_{i=1}^{m} \alpha_i - \sum_{i=1}^{m} \alpha_i y_i \left( \sum_{j=1}^{m} \alpha_j y_j x_j^T \right) x_i - b \sum_{i=1}^{m} \alpha_i y_i
L(α)=21i=1∑mj=1∑mαiαjyiyjxiTxj+i=1∑mαi−i=1∑mαiyi(j=1∑mαjyjxjT)xi−bi=1∑mαiyi
注意到第二项 ∑ i = 1 m α i \sum_{i=1}^{m} \alpha_i ∑i=1mαi 直接保持不变,因为它不依赖于 w w w 或 ( b )。
最后,第三项中的 ∑ j = 1 m α j y j x j T x i \sum_{j=1}^{m} \alpha_j y_j x_j^T x_i ∑j=1mαjyjxjTxi 和第一项中当 ( i = j ) 时是相同的项,但它们有相反的符号。因此,当我们合并第一项和第三项时,会发现这些项相互抵消,只剩下当 i ≠ j i \neq j i=j 时的项。同时省略 ( b ) 的项后,得到最终的目标函数:
L ( α ) = ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j L(\alpha) = \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^T x_j L(α)=i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj
这就是对偶问题的目标函数,我们需要对它关于
α
\alpha
α 进行最大化,同时满足
α
i
≥
0
\alpha_i \geq 0
αi≥0 和
∑
i
=
1
m
α
i
y
i
=
0
\sum_{i=1}^{m} \alpha_i y_i = 0
∑i=1mαiyi=0 这两个约束条件。通过解决这个对偶问题,我们可以找到最优的
α
\alpha
α 值,然后计算出
w
w
w 和 ( b ),从而确定最优的分类超平面。
所以最终得到:
max
α
(
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
)
\max_{\alpha} \left( \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^T x_j \right)
αmax(i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj)
s.t. ∑ i = 1 m α i y i = 0 , \text{s.t.}\sum_{i=1}^{m} \alpha_i y_i = 0, s.t.i=1∑mαiyi=0,
α i ≥ 0 , i = 1 , 2 , … , m . \alpha_i \geq 0, \quad i = 1, 2, \ldots, m. αi≥0,i=1,2,…,m.
直接带入
w
=
∑
i
=
1
m
α
i
y
i
x
i
w = \sum_{i=1}^{m} \alpha_i y_i x_i
w=∑i=1mαiyixi 得到模型
f
(
x
)
=
w
T
x
+
b
=
∑
i
=
1
m
α
i
y
i
x
i
T
x
+
b
f(x) = \mathbf{w}^T \mathbf{x} + b = \sum_{i=1}^{m} \alpha_i y_i \mathbf{x}_i^T \mathbf{x} + b
f(x)=wTx+b=i=1∑mαiyixiTx+b
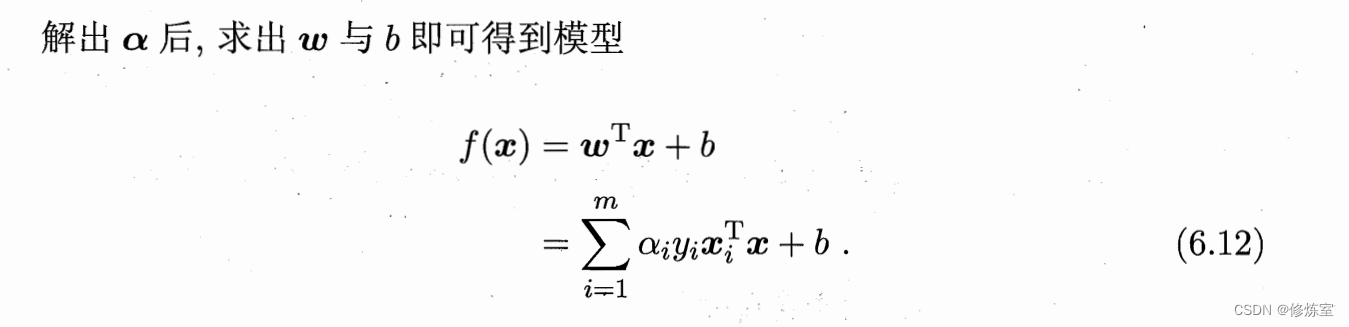
问题六:SVM中得到KKT条件的过程

KKT条件的推导
KKT条件来自于拉格朗日函数 ( L ) 的优化,特别是其对偶问题的解。它们包括:
- 原始问题的约束必须满足:这意味着 y i ( w T x i + b ) ≥ 1 y_i(w^T x_i + b) \geq 1 yi(wTxi+b)≥1 必须对所有 ( i ) 成立。
- 拉格朗日乘子必须非负: α i ≥ 0 \alpha_i \geq 0 αi≥0。
- 互补松弛性:对于每一个 α i \alpha_i αi,我们必须有 α i ( y i ( w T x i + b ) − 1 ) = 0 \alpha_i (y_i(w^T x_i + b) - 1) = 0 αi(yi(wTxi+b)−1)=0。