交换排序-冒泡排序 快速排序

news2024/11/23 2:15:17

目录

3.1 冒泡排序

3.2 快速排序

Hoare版本快速排序

挖坑法快速排序

前后指针法快速排序

快速排序优化-三数取中法

快速排序非递归

3.1 冒泡排序

思想：升序情况下：左边大于右边就进行交换，每一次把最大的放在最后一位。

void Swap(int* p1, int* p2){
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}
void BubbleSort(int* a, int n){
    //int a[] = {6,7,2,1,9,4};
    int end = n;//end后方均有序
    while (end) {
        int flag = 1;//假设已经排序成功
        for (int i = 0; i < n-1; i++) {
            if(a[i] > a[i+1]){
                flag = 0;//发生交换就说明无序
                Swap(&a[i], &a[i+1]);
            }
        }
        if(flag == 1) break;//说明没有发生交换——》已经有序
        //跳出循环
        end--;
    }
}

3.2 快速排序

Hoare版本快速排序

Hoare版本快速排序基本思想：取一值为key（一般取第一个数为key），在利用左右指针（双指针法），先右指针（right）找比key小的数，再左指针（left）找比key大的数据。如果找到了就交换左右指针的数据，当左右指针相遇的时候，就将相遇的数据与key进行交换，完成一次排序。接着对key的左边部分进行排序，方法与前相同，再对key右边排序，方法与前相同。由此可见，这是一个递归。

以接下来数组排序为例

int a[] = {9,5,6,3,15,13,32,18};

代码如下：

intPartSort(int* a,int left,int right){
	int key = left;
	//左找大 右找小
	while (left < right) {
		//右找小
		while (left < right && a[right] >= a[key]) {
			right--;
		}
		//左找大
		while (left < right && a[left] <= a[key]) {
			left++;
		}
		//交换左右指针数据
		Swap(&a[left], &a[right]);
	}
	//交换key值
	Swap(&a[key], &a[left]);
	return left;
}


voidQuickSort(int* a,int left,int right){
	if(left >= right){
		return;
	}
	int key = PartSort(a, left, right);
	QuickSort(a, left, key-1);
	QuickSort(a, key+1, right);
}

Hoare版本问题分析

1⃣️ 对于key值，一般取首元素作为key值，当然也可以使用最后元素作为key值，需要注意的是，当使用首元素作为key值的时候，left一定取在首元素（即key所在位置）位置，如果不在则会出现以下情况

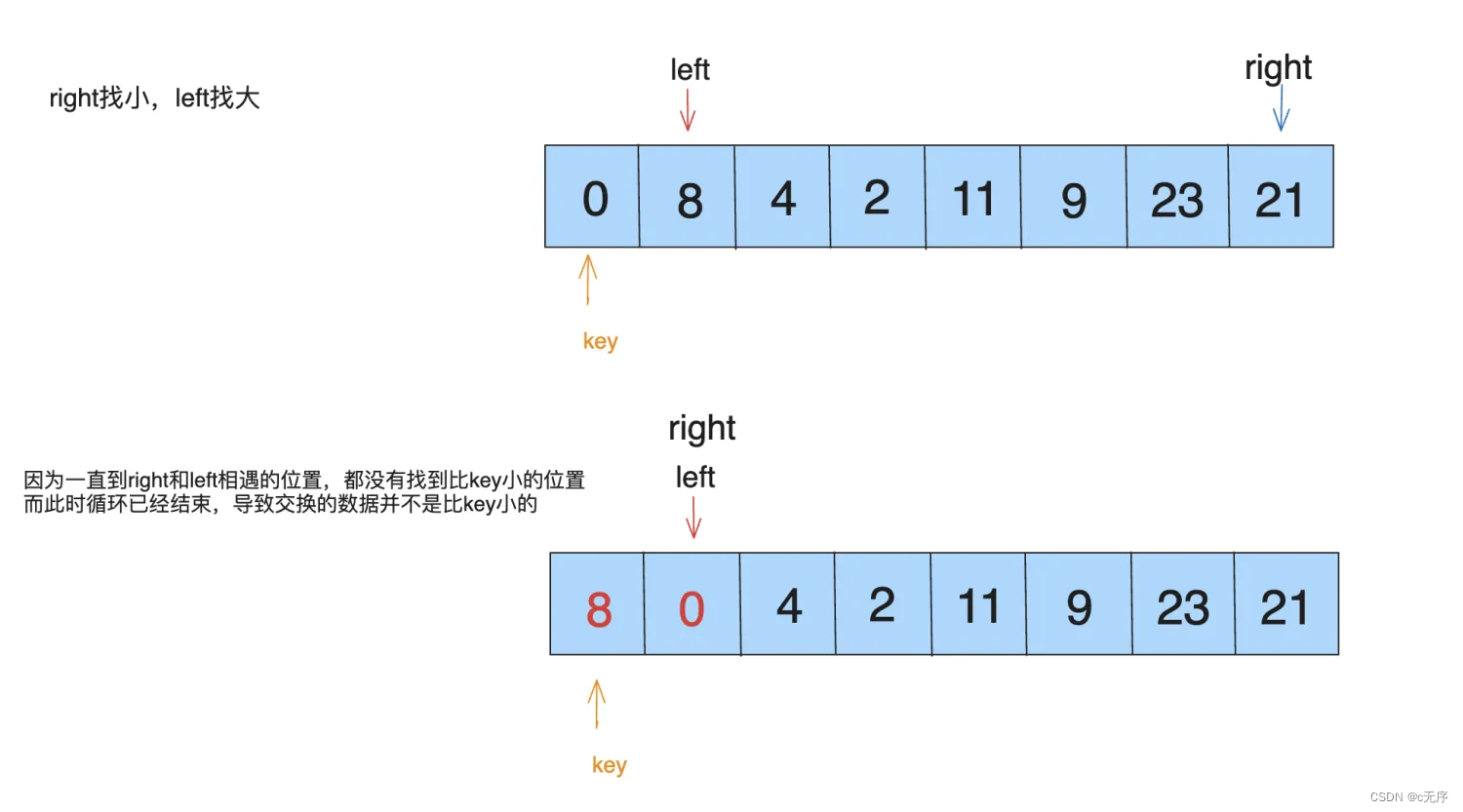
2⃣ ️当left指针和right指针移动的时候，一定要包含等于情况。如果不等于则出现以下情况 

 

3⃣ 递归结束条件分析，为什么是left >= right，就返回?

当二分下去后只剩一个数或者一个数都没有的时候就是有序，无需排序。如果只有等于，当某边为空的时候，此时传过来的key值为0，且key = left 那么传到下一个递归区间就变成了【0，-1】显然不和规矩，因此必须加 > 。

if(left >= right){
	return;
}️

挖坑法快速排序

挖坑法快速排序与Hoare版本的快速排序相比没有效率上的优化。

其基本思想是：从数据中随机选出一值为key，记录key的值，而该值的位置也是挖坑法中的坑（hole），接着利用左右指针，left在数组第一位，right在最后一位，两边向中间走，此时并没有规定谁先走，即可以left先走也可以right先走。我们假设right先走，先right找小（比key小），找到之后用right所指的数值覆盖hole的数值，再更新hole的位置到right上；再left走，找比key大的数值，找到之后，用left所指的数值覆盖hole的数值，再更新hole的位置到left上，与此反复直到两指针相遇，第一趟排序结束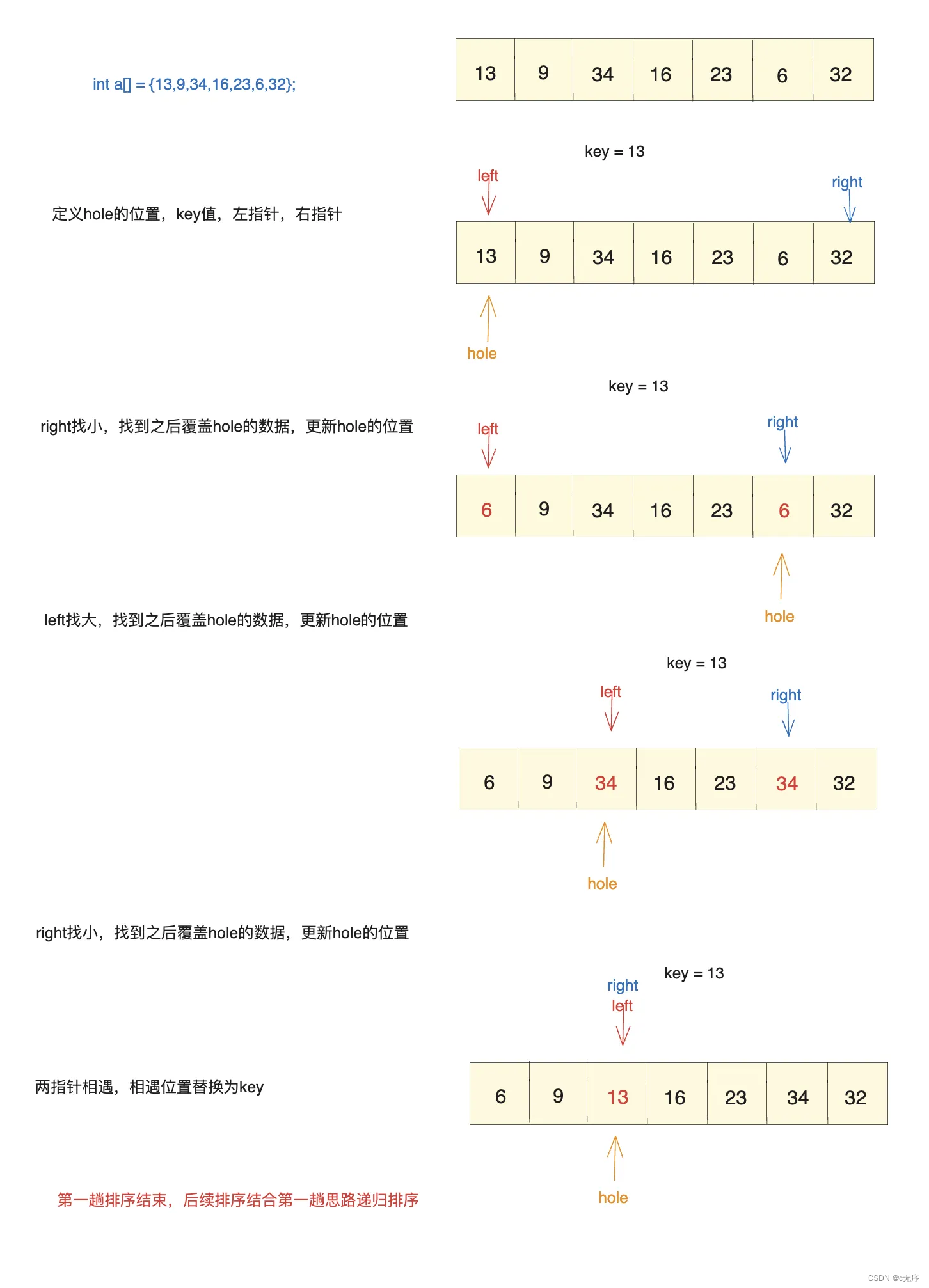

//快速排序3⃣️-挖坑法
int PartSort_DigHole(int* a, int left, int right){
    int hole = left;
    int key = a[left];
    while (left < right) {
        //右找小
        while (left < right && a[right] >= key) {
            right--;
        }
        int ahole = a[hole];
            a[hole] = a[right];
            hole = right;
        
        //左找大
        while (left < right && a[left] <= key) {
            left++;
        }
        ahole = a[hole];
            a[hole] = a[left];
            hole = left;
  
    }
    
    a[hole] = key;
    return hole;
    
}
void QuickSort_DigHole(int* a, int left, int right){
    if(left >= right){
        return;
    }
    
    int hole = PartSort_DigHole(a,left,right);
    QuickSort_DigHole(a,left,hole-1);
    QuickSort_DigHole(a,hole+1,right);
}

前后指针法快速排序

前后指针法快速排序，在效率上和挖坑法和Hoare快速排序效率所差无几。

其基本思想为：定义一个值为key（一般选第一个值为key），定义前指针（prev）后指针（cur）。先cur指针找比key小的数据，找到了就停下，在prev找比key大的数据，找到了就停下，交换前后指针数据。继续移动cur指针，直到cur指针超出排序个数（数组范围），交换prev与key的位置，完成一次排序，在如前两个方法一样进行递归排序。

以下是代码优化版

//快速排序2⃣️ 双指针法
void QuickSort2(int* a, int left, int right){
    int prev = left;
    int cur = left+1;
    int keyi = left;
    
    
    if(left >= right){
        return;
    }
    
    while (cur <= right) {
        //++prev != cur) 解决了自身交换的问题
        if(a[cur] < a[keyi] && ++prev != cur){
            Swap(&a[cur], &a[prev]);
        }
        cur++;
    }
    Swap(&a[prev], &a[keyi]);
    keyi = prev;
   
    
    //[left,keyi-1] key [keyi+1,right]
    QuickSort2(a,left,keyi-1);
    QuickSort2(a, keyi+1, right);//写递归一定要有出口
}

快速排序优化-三数取中法

取中的是key的位置不再是首元素，而是中间（首元素下标和尾元素下表之和的一半），确保数据存在大量数据或者有序情况下进行优化。

int GetMidi(int* a, int left, int right){
    int mid = (left + right)/2;
    if(a[left] < a[mid]){
        if(a[left] > a[right]){
            return left;
        }else if(a[right] > a[mid]){
            return mid;
        }else{
            return right;
        }
    }else{//a[left] > a[mid]
        if(a[right] < a[mid]){
            return mid;
        }else if (a[right] > a[left]){
            return left;
        }else{
            return right;
        }
    }
}

//快速排序1 右找小 左找大
// 时间复杂度：O(N*logN)
// 什么情况快排最坏：有序/接近有序 ->O(N^2)
// 但是如果加上随机选key或者三数取中选key，最坏情况不会出现，所以这里不看最坏
// 小区间优化
// 面试让你手撕快排，不要管三数取中和小区间优化
// Hoare
void QuickSort1(int* a, int left, int right){
    // 区间只有一个值或者不存在就是最小子问题
    if(left >= right) return;
    
    //1⃣️随机取keyi
//    srand((unsigned int)time(NULL));
//    int randi = rand()%(right-left+1);
//    randi += left;
//    Swap(&a[randi], &a[left]);
    
    //2⃣️三数取中法
    int keymid = GetMidi(a,left,right);
    Swap(&a[keymid], &a[left]);
    
    int keyi = left;
    int begin = left;
    int end = right;
    while (left < right) {
        //右边找小
        while (left < right && a[right]  >= a[keyi]) {
            --right;
        }
        //左边找大
        while (left < right && a[left] <= a[keyi]) {
            ++left;
        }
        Swap(&a[left], &a[right]);
    }
    
    Swap(&a[left], &a[keyi]);
    keyi = left;
    QuickSort1(a,begin,keyi-1);
    QuickSort1(a,keyi+1,end);
}

快速排序非递归

//
//  Stack.h
//  栈
//
//  Created by 南毅 on 2024/2/15.
//

#ifndef Stack_h
#define Stack_h

#include <stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>


#endif /* Stack_h */

typedef int STDataType;

typedef struct Stack{
    STDataType *a;
    int top;
    int capacity;
}ST;

void STInit(ST* ps);
void STDestroy(ST* ps);

void STPush(ST* ps, STDataType x);
void STPop(ST* ps);
STDataType STTop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);


//
//  Stack.c
//  栈
//
//  Created by 南毅 on 2024/2/15.
//

#include "Stack.h"
void STInit(ST* ps){
    assert(ps);
    ps->a = NULL;
    ps->top = ps->capacity = 0 ;
}

void STDestory(ST* ps){
    assert(ps);
    free(ps->a);
    ps->a = NULL;
    ps->top = ps->capacity = 0;
}

void STPush(ST* ps, STDataType x){
    assert(ps);
    
    if(ps->top==ps->capacity){
        int newcapacity = ps->capacity == 0 ? 4 : ps->capacity*2;
        STDataType* tmp = realloc(ps->a, newcapacity * sizeof(STDataType));
        if(tmp == NULL){
            perror("relloc fail");
            return;
        }
        
        ps->a = tmp;
        ps->capacity = newcapacity;
        
    }
    ps->a[ps->top++] = x;
    
}

void STPop(ST* ps){
    assert(ps);
    assert(!STEmpty(ps));
    ps->top--;
}

STDataType STTop(ST* ps){
    assert(ps);
    assert(!STEmpty(ps));
    return ps->a[ps->top-1];
}

int STSize(ST* ps){
    assert(ps);
    return ps->top;
}

bool STEmpty(ST*ps){
    assert(ps);
    return ps->top==0;
}

//快速排序 非递归
void QuickSortNonR(int* a, int left, int right){
    ST st;
    STInit(&st);
    STPush(&st, right);
    STPush(&st, left);
    
    while (!STEmpty(&st)) {
        int begin = STTop(&st);
        STPop(&st);
        int end = STTop(&st);
        STPop(&st);
        
        //单躺排序
        int prev = begin;
        int cur = begin+1;
        int keyi = begin;
        
        
        while (cur <= end) {
            //++prev != cur) 解决了自身交换的问题
            if(a[cur] < a[keyi] && ++prev != cur){
                Swap(&a[cur], &a[prev]);
            }
            cur++;
        }
        Swap(&a[prev], &a[keyi]);
        keyi = prev;
        
        //[begin,keyi-1] keyi [keyi+1,end]
        if(keyi+1 < end){
            STPush(&st, end);
            STPush(&st, keyi+1);
        }
        
        if(begin < keyi-1){
            STPush(&st, keyi-1);
            STPush(&st, begin);
        }
        
    }
    
   //STDestroy(&st);
}

快速排序的时间复杂度为O(N\times log_{2}{N})，空间复杂度为O(log_{2}{N})，属于不稳定算法

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1633272.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Unity100个实用小技巧】Unity接入微信SDK

【Unity100个实用小技巧】Unity接入微信SDK

前言 为了实现Unity接入微信排行榜,记录一下&#xff0c;为了以后用&#xff0c;本篇文章是对于使用中的一些疑惑点记录。完整流程官方和下面链接都有&#xff0c;补充一些&#xff0c;其他文档中未提到的。 步骤 必要步骤 一. 微信转小游戏 勾选 【使用好友关系链】 二. 看下…
阅读更多...
（06）vite与ts的结合

（06）vite与ts的结合

文章目录 系列全集package.json在根目录创建 tsconfig.json 文件在根目录创建 vite.config.ts 文件index.html额外的类型声明 系列全集 &#xff08;01&#xff09;vite 从启动服务器开始 &#xff08;02&#xff09;vite环境变量配置 &#xff08;03&#xff09;vite 处理 c…
阅读更多...
基于springboot+vue+Mysql的时间管理系统

基于springboot+vue+Mysql的时间管理系统

开发语言&#xff1a;Java框架&#xff1a;springbootJDK版本&#xff1a;JDK1.8服务器&#xff1a;tomcat7数据库&#xff1a;mysql 5.7&#xff08;一定要5.7版本&#xff09;数据库工具&#xff1a;Navicat11开发软件&#xff1a;eclipse/myeclipse/ideaMaven包&#xff1a;…
阅读更多...
基于双层优化的电动汽车优化调度研究(附matlab程序)

基于双层优化的电动汽车优化调度研究(附matlab程序)

基于双层优化的电动汽车优化调度研究 0.代码链接 基于双层优化的电动汽车优化调度研究(matlab程序)资源-CSDN文库 1.简述 关键词&#xff1a;双层优化 选址定容 输配协同 时空优化 参考文档&#xff1a;《考虑大规模电动汽车接入电网的双层优化调度策略_胡文平》…
阅读更多...
机器学习-11-卷积神经网络-基于paddle实现神经网络

机器学习-11-卷积神经网络-基于paddle实现神经网络

文章目录 总结参考本门课程的目标机器学习定义第一步&#xff1a;数据准备第二步&#xff1a;定义网络第三步&#xff1a;训练网络第四步&#xff1a;测试训练好的网络 总结 本系列是机器学习课程的系列课程&#xff0c;主要介绍基于paddle实现神经网络。 参考 MNIST 训练_副…
阅读更多...
C# Form1.cs 控件全部丢失的问题解决

C# Form1.cs 控件全部丢失的问题解决

在应用C#开发程序时&#xff0c;代码写了一堆&#xff0c;等调试时&#xff0c;点开 Form1.cs窗体时&#xff0c;出现如下提示。点击忽略并继续是&#xff0c;整个窗体控件全部丢失。 初次遇到这个问题&#xff0c;很容易进入到误区&#xff0c;以为窗体控件真的全部丢失了&am…
阅读更多...
算法入门ABC

算法入门ABC

前言 初学算法时真的觉得这东西晦涩难懂&#xff0c;貌似毫无用处&#xff01;后来的后来&#xff0c;终于渐渐明白搞懂算法背后的核心思想&#xff0c;能让你写出更加优雅的代码。就像一首歌唱的那样&#xff1a;后来&#xff0c;我总算学会了如何去爱&#xff0c;可惜你早已远…
阅读更多...
Linux磁盘分区与管理

Linux磁盘分区与管理

标题日期版本说明署名 Linux磁盘分区与管理 2024.4.29 v0.0.0*******LGB 目标&#xff1a;能够熟练掌握Linux系统磁盘分区管 操作系统&#xff1a;Centos Stream 9 实验过程&#xff1a; 1.首先我们先新建一块磁盘。 2.我们先对新建磁盘进行分区。 3.输入n 创建分区&#xf…
阅读更多...
Llama3 在线试用与本地部署

Llama3 在线试用与本地部署

美国当地时间4月18日&#xff0c;Meta 开源了 Llama3 大模型&#xff0c;目前开源版本为 8B 和 70B 。Llama 3 模型相比 Llama 2 具有重大飞跃&#xff0c;并在 8B 和 70B 参数尺度上建立了 LLM 模型的新技术。由于预训练和后训练的改进&#xff0c;Llama3 模型是目前在 8B 和 …
阅读更多...
React、React Router 和 Redux 常用Hooks 总结，提升您的开发效率！

React、React Router 和 Redux 常用Hooks 总结，提升您的开发效率！

Hooks 是 React 16.8 中引入的一种新特性&#xff0c;它使得函数组件可以使用 state 和其他 React 特性&#xff0c;从而大大提高了函数组件的灵活性和功能性。下面分别总结React、React Router 、Redux中常用的Hooks。 常用Hooks速记 React Hooks useState&#xff1a;用于…
阅读更多...
vue为遍历生成的表单设置ref属性

vue为遍历生成的表单设置ref属性

最近在写表单重置的时候出现了问题&#xff0c;在this.$refs[formName].resetFields();的时候卡了很久。 经过网上的搜索终于解决的问题&#xff01; 对于不需要遍历的表单 这是vue代码&#xff1a; <el-dialog title"段落描述" :visible.sync"dialogFormV…
阅读更多...
流水线工作流程

流水线工作流程

java编译命令&#xff1a; java -jar xxx.jar (其它参数已忽略) docker镜像构建命令&#xff1a; docker build -t [镜像名称:latest] -f 指定[Dockerfile] [指定工作目录] 推送镜像 jenkinsfile: 主要流程登录镜像仓库&#xff0c;打包镜像&#xff0c;推送到镜像仓库
阅读更多...
MySql 主从同步-在原来同步基础上增加历史数据库

MySql 主从同步-在原来同步基础上增加历史数据库

在MySql已经主从同步的后&#xff0c;由于有新的需求再增加1个历史数据库&#xff0c;要改原来的1个变成现在的2个数据库。在官网并没有找到类似的场景&#xff08;官方同步多个数据是从一开始就设置&#xff0c;不是后续增加的&#xff09;&#xff0c;只能结合以往的经验自己…
阅读更多...
第三方软件测试机构-科技成果评价测试

第三方软件测试机构-科技成果评价测试

科技成果评价测试是对科研成果的工作质量、学术水平、实际应用和成熟程度等方面进行的客观、具体、恰当的评价过程。这一评价过程有助于了解科技成果的质量和水平&#xff0c;以及其在学术和应用方面的价值和潜力。 科技成果评价测试主要包括以下几个方面&#xff1a; 工作质量…
阅读更多...
OpenVoice: Versatile Instant Voice Cloning

OpenVoice: Versatile Instant Voice Cloning

OpenVoice&#xff1a;多功能即时语音克隆 摘要 OpenVoice是一种多功能的即时声音克隆方法&#xff0c;它只需要参考说话者的一小段音频就可以复制他们的声音并以多种语言生成语音。OpenVoice 在解决以下领域中的开放性挑战方面代表了重大进展&#xff1a;1) 灵活的声音风格控…
阅读更多...
【1762】java校园单车投放系统Myeclipse开发mysql数据库web结构jsp编程servlet计算机网页项目

【1762】java校园单车投放系统Myeclipse开发mysql数据库web结构jsp编程servlet计算机网页项目

一、源码特点 java校园单车投放管理系统是一套完善的java web信息管理系统 采用serlvetdaobean&#xff0c;对理解JSP java编程开发语言有帮助&#xff0c;系统具有完整的源代码和数据库&#xff0c;系统主要采用B/S 模式开发。开发环境为TOMCAT7.0,Myeclipse8.5开发&#…
阅读更多...
面试题：两阶段提交与三阶段提交的区别？

面试题：两阶段提交与三阶段提交的区别？

主要区别有以下几点&#xff1a; 增加了一个询问阶段&#xff0c;问了下&#xff0c;你能不不能行&#xff1f;加入了超时机制 2PC&#xff08;二阶段提交协议&#xff09; 2PC&#xff0c;两阶段提交&#xff0c;将事务的提交过程分为资源准备和资源提交两个阶段&#xff0c;…
阅读更多...
Linux配置双网卡，1NAT 2桥接，ARM板上网

Linux配置双网卡，1NAT 2桥接，ARM板上网

1、简介 版本型号&#xff1a;ubuntu18.04 ARM板型号&#xff1a;6ull本文主要记录配置第一次ubuntu与arm板连接的nfs配置和ARM板上网的配置&#xff0c;按照配置网络、配置nfs系统、给板子连网 顺序进行。该配置的前提是创建ubuntu系统的网络配置选择的是NAT模式&…
阅读更多...
算法设计优化——起泡排序

算法设计优化——起泡排序

文章目录 0.概述1 起泡排序&#xff08;基础版&#xff09;1.1 算法分析1.2 算法实现1.3 重复元素与稳定性1.4 复杂度分析 2 起泡排序&#xff08;改进版&#xff09;2.1 目标2.2 改进思路2.3 实现2.4 复杂度分析 3 起泡排序&#xff08;改进版2&#xff09;3.1 目标3.1 改进思…
阅读更多...
鸿蒙内核源码分析(汇编基础篇) | CPU在哪里打卡上班

鸿蒙内核源码分析(汇编基础篇) | CPU在哪里打卡上班

本篇通过拆解一段很简单的汇编代码来快速认识汇编&#xff0c;为读懂鸿蒙汇编打基础.系列篇后续将逐个剖析鸿蒙的汇编文件. 汇编很简单 第一&#xff1a; 要认定汇编语言一定是简单的&#xff0c;没有高深的东西&#xff0c;无非就是数据的搬来搬去&#xff0c;运行时数据主要…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023