代码随想录算法训练营第五天:哈希表的初步认识
数组就是简单的哈希表,但是数组的大小可不是无限开辟的
前言
我们已经学习了数组、字符串、链表等数据结构,但是大家有没有发现,如果我们想要找到其中某个元素或者节点,需要从索引为0的位置或者表头开始,逐一进行比较,直到找到相等的位置或者末尾才会结束。
那是否可以避免之前的比较,直接通过要查找的记录直接找到其存储位置呢?
是有的,可以通过“哈希表”来实现,哈希表是根据关键码key的值而直接进行访问的数据结构。
哈希表的作用是快速判断一个元素是否出现在集合里,它的核心思想是在关键码和存储位置之间建立一个确定的对应关系f, 使得每个关键字key对应一个存储位置,而这个对应关系,称之为散列函数(哈希函数)。
其实数组就是一张哈希表,哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素。
哈希表来解决问题的时候,一般选择以下三种数据结构。
- 数组
-
set集合 -
map映射
哈希表
关于哈希表的更多介绍,可以移步至代码随想录官方网站查看
哈希表可以将其比喻为一个大抽屉,抽屉里面有很多小格子。每个格子可以用来存放一些东西。
- 抽屉编号: 抽屉有编号,这个编号就是数据的
key,我们通过这个key来找到对应的抽屉。 - 散列函数: 哈希表使用一种特殊的函数(哈希函数),来决定数据应该放在哪个抽屉里。这个函数将数据的名字
key转换成一个数字,然后根据这个数字来选择一个抽屉。 - 抽屉里的物品: 在每个抽屉里,可以放一些东西,这些东西就是我们要存储的数据。
- 解决冲突: 有时候不同的
key经过散列函数后可能会得到相同的编号,这就是冲突。哈希表有方法来处理这些冲突。 - 快速查找: 当我们需要找到某个数据时,哈希表可以通过名字
key快速地找到对应的抽屉,然后取出里面的数据,这个操作非常快速,就像从抽屉中拿出东西一样。
Set
关于
unordered_set,multiset<span> </span>的区别,,可以移步至代码随想录官方网站查看
和数学中的集合一样,C++中的集合set用于允许存储一组不重复的元素, 并且元素的值按照有序排列, set基于红黑树实现,支持高效的关键字查询操作, 可以用来检查一个给定关键字是否在set中。
无序集合unordered-set类似于集合(Set),但不会按照元素的值进行排序,而是由哈希函数的结果决定的。
multiset 则是一个用于存储一组元素,允许元素重复,并按照元素的值进行有序排列的集合。
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 |
|---|---|---|---|
| std::set | 红黑树 | 有序 | 否 |
| std::multiset | 红黑树 | 有序 | 是 |
| std::unordered_set | 哈希表 | 无序 | 否 |
map的基本介绍
我们常常把map称之为映射,就是将一个元素(通常称之为key键)与一个相对应的值(通常称之为value)关联起来,比如说一个学生的姓名(key)有与之对应的成绩(value),它们是一一对应的,就好像一把钥匙开一扇门,在map中键是唯一的,也只有一个唯一的确定的值。
在C++中, map 提供了以下三种数据结构,其底层实现以及优劣如下表所示:
map中的键是唯一的,但是multimap则没有此限制
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 |
|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 |
| std::multimap | 红黑树 | key有序 | key可重复 |
| std::unordered_map | 哈希表 | key无序 | key不可重复 |
std::unordered_map 的key值存储是无序的,底层实现为哈希表,查找速度更快,如果不需要排序而只是快速查找键对应的值,可以考虑使用。
std::map 和std::multimap 的底层实现是红黑树,它的key值存储是有序的,如果需要对键值对进行自定义排序,可以考虑使用std::map。
map的使用
使用映射容器需要引入头文件<unordered_map>或者<map>
// 引入unordered_map头文件,包含unordered_map类型
#include <unordered_map>
// 引入map头文件,包含map类型和multimap类型
#include <map>
想要声明map映射关系,需要指定键的类型和值的类型。
// 声明一个整数类型映射到整数类型的 无序映射
unordered_map<int, int> uMap;
// 声明一个将字符串映射到整数的`map`,可以这样声明:
map<string, int> myMap;
想要插入键值对key-value, 需要使用insert()函数或者使用[]操作符来插入。如果键不存在,[]操作符将会创建一个新的键值对,将其插入到map中,并将值初始化为默认值(对于整数来说,默认值是0)。
uMap[0] = 10;
uMap[10] = 0;
myMap["math"] = 100;
myMap["english"] = 80;
和set类似,可以使用find函数来检查某个键是否存在于map中,它会返回一个迭代器。如果键存在,迭代器指向该键值对,否则指向map的末尾。
if (myMap.find("math") != myMap.end()) {
// 键存在
} else {
// 键不存在
}
你可以使用范围for循环来遍历map中的所有键值对,进行各种操作。
for(const pair<int,int>& kv:umap) {
}
当使用范围for循环遍历map时,我们需要声明一个变量kv来存储每个键值对。这个变量的类型通常是pair类型,下面就让我们详细解释一下const pair<int,int>& kv:umap
const用于声明一个不可修改的变量,这意味着一旦变量被初始化,就不能再修改其值。常量通常用大写字母表示
因为const声明的变量一旦创建后就无法修改值,所以必须初始化。
const double PI = 3.1415926;
在这里,const关键字表示你只能读取容器中的元素,而不能修改它们。
而pair<int, int>定义了kv也就是键值对的数据类型是pair, C++中的pair类型会将两个不同的值组合成一个单元, 常用于存储键值对,创建pair的时候,也必须提供两个类型名,比如上面的pair对象,两个值的类型都是int, 在使用时通过first 和 second 成员来访问 pair 中的第一个和第二个元素, 它的 first 成员存储键,而 second 成员存储值。
&:这个符号表示kv是一个引用(reference),而不是值的拷贝, 如果不使用引用的话,那在每次循环迭代中都会重新创建一个新的pair对象来复制键值对,而这会导致不必要的内存分配和拷贝操作。
范围for循环
C++11引入了范围for循环,用于更方便地遍历容器中的元素。这种循环提供了一种简单的方式来迭代容器中的每个元素,而不需要显式地使用迭代器或索引。
for (类型 变量名 : 容器) {
// 在这里使用一个变量名,表示容器中的每个元素
}
比如下面的代码就表示使用范围for循环遍历一个容器
std::vector<int> numbers = {1, 2, 3, 4, 5};
// 使用范围for循环遍历向量中的元素
for (int num : numbers) {
std::cout << num << " ";
}
范围for循环不会修改容器中的元素,它只用于读取元素。如果需要修改容器中的元素,需要使用传统的for循环或其他迭代方式。
此外,还可以使用auto关键字来让编译器自动推断元素的类型,这样代码会更通用
// 使用auto关键字自动推断元素的类型
for (auto num : numbers) {
std::cout << num << " ";
}
242.有效的字母异位词
力扣题目链接(opens new window)
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1: 输入: s = “anagram”, t = “nagaram” 输出: true
示例 2: 输入: s = “rat”, t = “car” 输出: false
说明: 你可以假设字符串只包含小写字母。
算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** :学透哈希表,数组使用有技巧!Leetcode:242.有效的字母异位词 ****(opens new window)**** ,相信结合视频再看本篇题解,更有助于大家对本题的理解。
思路
先看暴力的解法,两层for循环,同时还要记录字符是否重复出现,很明显时间复杂度是 O(n^2)。
暴力的方法这里就不做介绍了,直接看一下有没有更优的方式。
数组其实就是一个简单哈希表,而且这道题目中字符串只有小写字符,那么就可以定义一个数组,来记录字符串s里字符出现的次数。
如果对哈希表的理论基础关于数组,set,map不了解的话可以看这篇:关于哈希表,你该了解这些!(opens new window)
需要定义一个多大的数组呢,定一个数组叫做record,大小为26 就可以了,初始化为0,因为字符a到字符z的ASCII也是26个连续的数值。
为了方便举例,判断一下字符串s= “aee”, t = “eae”。
操作动画如下:

定义一个数组叫做record用来上记录字符串s里字符出现的次数。
需要把字符映射到数组也就是哈希表的索引下标上,因为字符a到字符z的ASCII是26个连续的数值,所以字符a映射为下标0,相应的字符z映射为下标25。
再遍历 字符串s的时候,只需要将 s[i] - ‘a’ 所在的元素做+1 操作即可,并不需要记住字符a的ASCII,只要求出一个相对数值就可以了。 这样就将字符串s中字符出现的次数,统计出来了。
那看一下如何检查字符串t中是否出现了这些字符,同样在遍历字符串t的时候,对t中出现的字符映射哈希表索引上的数值再做-1的操作。
那么最后检查一下,record数组如果有的元素不为零0,说明字符串s和t一定是谁多了字符或者谁少了字符,return false。
最后如果record数组所有元素都为零0,说明字符串s和t是字母异位词,return true。
时间复杂度为O(n),空间上因为定义是的一个常量大小的辅助数组,所以空间复杂度为O(1)。
C++ 代码如下:
class Solution {
public:
bool isAnagram(string s, string t) {
int record[26] = {0};
for (int i = 0; i < s.size(); i++) {
// 并不需要记住字符a的ASCII,只要求出一个相对数值就可以了
record[s[i] - 'a']++;
}
for (int i = 0; i < t.size(); i++) {
record[t[i] - 'a']--;
}
for (int i = 0; i < 26; i++) {
if (record[i] != 0) {
// record数组如果有的元素不为零0,说明字符串s和t 一定是谁多了字符或者谁少了字符。
return false;
}
}
// record数组所有元素都为零0,说明字符串s和t是字母异位词
return true;
}
};
class Solution{
public:
bool isAnagram(string s, string t){
unordered_map <char ,int > mp;
if (s.size()!= t.size())return false;
for (int i = 0;i<s.size();i++){
mp[s[i]]++;
mp[t[i]]--;
}
for (auto i:mp) {
if (i.second != 0)
return false;
return true;
}
}
};//这是我模拟的代码
383. 赎金信
力扣题目链接(opens new window)
给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串,判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成,返回 true ;否则返回 false。
(题目说明:为了不暴露赎金信字迹,要从杂志上搜索各个需要的字母,组成单词来表达意思。杂志字符串中的每个字符只能在赎金信字符串中使用一次。)
注意:
你可以假设两个字符串均只含有小写字母。
canConstruct(“a”, “b”) -> false
canConstruct(“aa”, “ab”) -> false
canConstruct(“aa”, “aab”) -> true
#思路
这道题目和242.有效的字母异位词 **(opens new window)** 很像,242.有效的字母异位词 **(opens new window)** 相当于求 字符串a 和 字符串b 是否可以相互组成 ,而这道题目是求 字符串a能否组成字符串b,而不用管字符串b 能不能组成字符串a。
本题判断第一个字符串ransom能不能由第二个字符串magazines里面的字符构成,但是这里需要注意两点。
- 第一点“为了不暴露赎金信字迹,要从杂志上搜索各个需要的字母,组成单词来表达意思” 这里说明杂志里面的字母不可重复使用。
- 第二点 “你可以假设两个字符串均只含有小写字母。” 说明只有小写字母,这一点很重要
#暴力解法
那么第一个思路其实就是暴力枚举了,两层for循环,不断去寻找,代码如下:
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
for (int i = 0; i < magazine.length(); i++) {
for (int j = 0; j < ransomNote.length(); j++) {
// 在ransomNote中找到和magazine相同的字符
if (magazine[i] == ransomNote[j]) {
ransomNote.erase(ransomNote.begin() + j); // ransomNote删除这个字符
break;
}
}
}
// 如果ransomNote为空,则说明magazine的字符可以组成ransomNote
if (ransomNote.length() == 0) {
return true;
}
return false;
}
};
这里时间复杂度是比较高的,而且里面还有一个字符串删除也就是erase的操作,也是费时的,当然这段代码也可以过这道题。
哈希解法
因为题目说只有小写字母,那可以采用空间换取时间的哈希策略,用一个长度为26的数组来记录magazine里字母出现的次数。
然后再用ransomNote去验证这个数组是否包含了ransomNote所需要的所有字母。
依然是数组在哈希法中的应用。
一些同学可能想,用数组干啥,都用map完事了,其实在本题的情况下,使用map的空间消耗要比数组大一些的,因为map要维护红黑树或者哈希表,而且还要做哈希函数,是费时的!数据量大的话就能体现出来差别了。 所以数组更加简单直接有效!
代码如下:
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
int record[26] = {0};
//add
if (ransomNote.size() > magazine.size()) {
return false;
}
for (int i = 0; i < magazine.length(); i++) {
// 通过record数据记录 magazine里各个字符出现次数
record[magazine[i]-'a'] ++;
}
for (int j = 0; j < ransomNote.length(); j++) {
// 遍历ransomNote,在record里对应的字符个数做--操作
record[ransomNote[j]-'a']--;
// 如果小于零说明ransomNote里出现的字符,magazine没有
if(record[ransomNote[j]-'a'] < 0) {
return false;
}
}
return true;
}
};
bool canConstruct (char* ransomNote,char* magazine){
int hashmap[26] = {0};
while(*magazine != '\0') hashmap[*magazine++ % 26]++;
while(*ransomNote != '\0')hashmap[*ransomNote++ %26]--;
for (int i = 0;i< 26 ;i++){
if (hashmap[i] < 0)return false;
}
return true;
}
49.字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
提示:
-
1 <= strs.length <= 10<sup>4</sup> -
0 <= strs[i].length <= 100 -
strs[i] 仅包含小写字母
前言
两个字符串互为字母异位词,当且仅当两个字符串包含的字母相同。同一组字母异位词中的字符串具备相同点,可以使用相同点作为一组字母异位词的标志,使用哈希表存储每一组字母异位词,哈希表的键为一组字母异位词的标志,哈希表的值为一组字母异位词列表。
遍历每个字符串,对于每个字符串,得到该字符串所在的一组字母异位词的标志,将当前字符串加入该组字母异位词的列表中。遍历全部字符串之后,哈希表中的每个键值对即为一组字母异位词。
以下的两种方法分别使用排序和计数作为哈希表的键。
方法一:排序
由于互为字母异位词的两个字符串包含的字母相同,因此对两个字符串分别进行排序之后得到的字符串一定是相同的,故可以将排序之后的字符串作为哈希表的键。
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
// 定义无序映射以存储分组结果
unordered_map<string, vector<string>> mp;
// 遍历输入的字符串数组
for (string& str : strs) {
// 将当前字符串赋值给key
string key = str;
// 对key进行排序,作为同字母异序词的标识
sort(key.begin(), key.end());
// 将原始字符串添加到对应排序后的字符串的值中
mp[key].emplace_back(str);
}
// 定义二维字符串数组用于存储最终结果
vector<vector<string>> ans;
// 遍历映射,将每个键对应的值添加到结果数组中
for (auto it = mp.begin(); it != mp.end(); ++it) {
ans.emplace_back(it->second);
}
// 返回最终的结果数组
return ans;
}
};
官方结题思路的详细分析: 初始化一个空的 HashMap map。 遍历字符串数组 strs。对第一个字符串 "eat"执行: 将 “eat” 转换为字符数组 [‘e’, ‘a’, ‘t’] 对字符数组进行排序,得到 [‘a’, ‘e’, ‘t’] 使用排序后的字符数组创建 key “aet” 从 map 中获取 key 为 “aet” 的值,由于不存在,因此创建一个新的空列表 list = [] 将 “eat” 添加到 list 中,现在 list = [“eat”] 将 key 为 “aet”,value 为 [“eat”] 的键值对存入 map 对第二个字符串 “tea” 执行类似操作: 字符数组为 [‘t’, ‘e’, ‘a’],排序后为 [‘a’, ‘e’, ‘t’],key 为 “aet” 从 map 中获取 key 为 “aet” 的值,存在,为 [“eat”] 将 “tea” 添加到列表中,现在列表为 [“eat”, “tea”] 将更新后的列表存入 map,key 为 “aet” 对其余字符串 “tan”, “ate”, “nat”, “bat” 执行类似操作,最终 map 为: key 为 “aet”,value 为 [“eat”, “tea”, “ate”] key 为 “ant”,value 为 [“tan”, “nat”] key 为 “abt”,value 为 [“bat”] 从 map 中获取所有 value,构造结果列表,即 [ [“eat”, “tea”, “ate”], [“tan”, “nat”], [“bat”] ] 可以看到,通过将每个字符串排序作为 key,并存储字母异位词的字符串列表作为 value,算法成功将字母异位词分组了。这样的分组过程更加高效,避免了对每个字符串都进行两两比较的低效操作。
方法二:计数
由于互为字母异位词的两个字符串包含的字母相同,因此两个字符串中的相同字母出现的次数一定是相同的,故可以将每个字母出现的次数使用字符串表示,作为哈希表的键。
由于字符串只包含小写字母,因此对于每个字符串,可以使用长度为 262626 的数组记录每个字母出现的次数。需要注意的是,在使用数组作为哈希表的键时,不同语言的支持程度不同,因此不同语言的实现方式也不同。
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
// 自定义对 array<int, 26> 类型的哈希函数
auto arrayHash = [fn = hash<int>{}] (const array<int, 26>& arr) -> size_t {
return accumulate(arr.begin(), arr.end(), 0u, [&](size_t acc, int num) {
return (acc << 1) ^ fn(num);
});
};
unordered_map<array<int, 26>, vector<string>, decltype(arrayHash)> mp(0, arrayHash);
for (string& str: strs) {
array<int, 26> counts{};
int length = str.length();
for (int i = 0; i < length; ++i) {
counts[str[i] - 'a'] ++;
}
mp[counts].emplace_back(str);
}
vector<vector<string>> ans;
for (auto it = mp.begin(); it != mp.end(); ++it) {
ans.emplace_back(it->second);
}
return ans;
}
};
C++解题方法
-
decltype()指的是之前声明的变量类型,如decltye(x)返回x之前声明的变量类型。 -
array相比于vector, array是定长数组, vector是可变长度的数组。 -
arrayHash匿名函数,嵌套了一个匿名函数[fn = hash<int>{}]是初始化捕获列表,也就是说定义了一个auto fn = hash<int>{};供后续使用 默认是使用hash<T> 来实现的,但是hash没有办法去实现一个array的哈希,因此需要手动去构造一个哈希函数。本次构造哈希函数,是基于已有的hash去实现的,哈希碰撞概率几乎为0。arrayHash接受一个array<int, 26>类型的数组作为参数,并返回一个size_t类型的哈希值,这是因为cpp文档中规定hash<T>的Hash值必须是无符号整型size_t。 -
accumulate函数在头文件中,有三个形参:头两个形参指定要累加的元素范围,第三个形参则是累加的初值。第四个参数是累次运算的计算方法,如果没有给定则默认是加法,可以对上次的结果用本次的数字进行一定的计算后返回保存,[&]表示以引用的方式捕获作用域外所有的变量,两个参数中第一个参数是accumulate在这个指定的范围内前一段范围计算的值和哈希值一样是SIZE_T类型,后一个值是本次要操作的数字,在这个哈希算法中,每个元素通过fn(num)调用哈希函数对象来获取其哈希值,然后将之前累次运算结果左移一位(acc << 1)相当于乘2后与array中本次要操作的数num的哈希值进行异或操作(^)得到新的哈希值。最终,累次运算结果结果将作为这个数组的哈希值返回。
如对于eat这个单词,在accumulate函数中累次运算结果如下:
acc : 0 num: 1 acc << 1: 0 fn(num): 1 (acc << 1) ^ fn(num): 1 \newlineacc : 1 num: 0 acc << 1: 2 fn(num): 0 (acc << 1) ^ fn(num): 2 \newlineacc : 2 num: 0 acc << 1: 4 fn(num): 0 (acc << 1) ^ fn(num): 4 \newlineacc : 4 num: 0 acc << 1: 8 fn(num): 0 (acc << 1) ^ fn(num): 8 \newlineacc : 8 num: 1 acc << 1: 16 fn(num): 1 (acc << 1) ^ fn(num): 17 \newlineacc : 17 num: 0 acc << 1: 34 fn(num): 0 (acc << 1) ^ fn(num): 34 \newlineacc : 34 num: 0 acc << 1: 68 fn(num): 0 (acc << 1) ^ fn(num): 68 \newlineacc : 68 num: 0 acc << 1: 136 fn(num): 0 (acc << 1) ^ fn(num): 136 \newlineacc : 136 num: 0 acc << 1: 272 fn(num): 0 (acc << 1) ^ fn(num): 272 \newlineacc : 272 num: 0 acc << 1: 544 fn(num): 0 (acc << 1) ^ fn(num): 544 \newlineacc : 544 num: 0 acc << 1: 1088 fn(num): 0 (acc << 1) ^ fn(num): 1088 \newlineacc : 1088 num: 0 acc << 1: 2176 fn(num): 0 (acc << 1) ^ fn(num): 2176 \newlineacc : 2176 num: 0 acc << 1: 4352 fn(num): 0 (acc << 1) ^ fn(num): 4352 \newlineacc : 4352 num: 0 acc << 1: 8704 fn(num): 0 (acc << 1) ^ fn(num): 8704 \newlineacc : 8704 num: 0 acc << 1: 17408 fn(num): 0 (acc << 1) ^ fn(num): 17408 \newlineacc : 17408 num: 0 acc << 1: 34816 fn(num): 0 (acc << 1) ^ fn(num): 34816 \newlineacc : 34816 num: 0 acc << 1: 69632 fn(num): 0 (acc << 1) ^ fn(num): 69632 \newlineacc : 69632 num: 0 acc << 1: 139264 fn(num): 0 (acc << 1) ^ fn(num): 139264 \newlineacc : 139264 num: 0 acc << 1: 278528 fn(num): 0 (acc << 1) ^ fn(num): 278528 \newlineacc : 278528 num: 1 acc << 1: 557056 fn(num): 1 (acc << 1) ^ fn(num): 557057 \newlineacc : 557057 num: 0 acc << 1: 1114114 fn(num): 0 (acc << 1) ^ fn(num): 1114114 \newlineacc : 1114114 num: 0 acc << 1: 2228228 fn(num): 0 (acc << 1) ^ fn(num): 2228228 \newlineacc : 2228228 num: 0 acc << 1: 4456456 fn(num): 0 (acc << 1) ^ fn(num): 4456456 \newlineacc : 4456456 num: 0 acc << 1: 8912912 fn(num): 0 (acc << 1) ^ fn(num): 8912912 \newlineacc : 8912912 num: 0 acc << 1: 17825824 fn(num): 0 (acc << 1) ^ fn(num): 17825824 \newlineacc : 17825824 num: 0 acc << 1: 35651648 fn(num): 0 (acc << 1) ^ fn(num): 35651648
我们最终得到eat这个单词的哈希值是35651648. 你现在可能有一个问题了,为什么要搞这么复杂的哈希函数,直接累加不就完了,还用在里面再嵌套一个匿名函数吗,我说这当然是有必要的。你可以自己想想这样哈希函数的哈希碰撞问题,你所设想的这样一个哈希函数是否会导致两个单词不是易位次但是会得到相同的哈希值?如果是这样,那么你的哈希函数显然就是不合适的。事实证明不断扩大结果集有助于降低哈希冲突的概率,但这却并不表明我们可以完全避免哈希冲突,你不妨看看下面这个例子。事实上我们在本题中只是将结果集扩大到了2的26次方。
438.找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
示例 2:
输入: s = "abab", p = "ab" 输出: [0,1,2] 解释: 起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。 起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。 起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
下面带来labuladong的题解:
读完本文,你可以去力扣拿下如下题目:
76.最小覆盖子串
567.字符串的排列
438.找到字符串中所有字母异位词
3.无重复字符的最长子串
-----------
鉴于前文 二分搜索框架详解 的那首《二分搜索升天词》很受好评,并在民间广为流传,成为安睡助眠的一剂良方,今天在滑动窗口算法框架中,我再次编写一首小诗来歌颂滑动窗口算法的伟大:
 {:align=center}
{:align=center}
关于双指针的快慢指针和左右指针的用法,可以参见前文 双指针技巧汇总,本文就解决一类最难掌握的双指针技巧:滑动窗口技巧。总结出一套框架,可以保你闭着眼睛都能写出正确的解法。
说起滑动窗口算法,很多读者都会头疼。这个算法技巧的思路非常简单,就是维护一个窗口,不断滑动,然后更新答案么。LeetCode 上有起码 10 道运用滑动窗口算法的题目,难度都是中等和困难。该算法的大致逻辑如下:
int left = 0, right = 0;
while (right < s.size()) {
// 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
}
}
这个算法技巧的时间复杂度是 O(N),比字符串暴力算法要高效得多。
其实困扰大家的,不是算法的思路,而是各种细节问题。比如说如何向窗口中添加新元素,如何缩小窗口,在窗口滑动的哪个阶段更新结果。即便你明白了这些细节,也容易出 bug,找 bug 还不知道怎么找,真的挺让人心烦的。
所以今天我就写一套滑动窗口算法的代码框架,我连再哪里做输出 debug 都给你写好了,以后遇到相关的问题,你就默写出来如下框架然后改三个地方就行,还不会出 bug:
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
其中两处 ... 表示的更新窗口数据的地方,到时候你直接往里面填就行了。
而且,这两个 ... 处的操作分别是右移和左移窗口更新操作,等会你会发现它们操作是完全对称的。
言归正传,下面就直接上四道 LeetCode 原题来套这个框架,其中第一道题会详细说明其原理,后面四道就直接闭眼睛秒杀了。
本文代码为 C++ 实现,不会用到什么编程方面的奇技淫巧,但是还是简单介绍一下一些用到的数据结构,以免有的读者因为语言的细节问题阻碍对算法思想的理解:
unordered_map 就是哈希表(字典),它的一个方法 count(key) 相当于 Java 的 containsKey(key) 可以判断键 key 是否存在。
可以使用方括号访问键对应的值 map[key]。需要注意的是,如果该 key 不存在,C++ 会自动创建这个 key,并把 map[key] 赋值为 0。
所以代码中多次出现的 map[key]++ 相当于 Java 的 map.put(key, map.getOrDefault(key, 0) + 1)。
一、最小覆盖子串
LeetCode 76 题,Minimum Window Substring,难度 Hard:
 {:align=center}
{:align=center}
就是说要在 S(source) 中找到包含 T(target) 中全部字母的一个子串,且这个子串一定是所有可能子串中最短的。
如果我们使用暴力解法,代码大概是这样的:
for (int i = 0; i < s.size(); i++)
for (int j = i + 1; j < s.size(); j++)
if s[i:j] 包含 t 的所有字母:
更新答案
思路很直接,但是显然,这个算法的复杂度肯定大于 O(N^2) 了,不好。
滑动窗口算法的思路是这样:
1、我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引左闭右开区间 [left, right) 称为一个「窗口」。
2、我们先不断地增加 right 指针扩大窗口 [left, right),直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
3、此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right),直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
4、重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解, 也就是最短的覆盖子串。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动,这就是「滑动窗口」这个名字的来历。
下面画图理解一下,needs 和 window 相当于计数器,分别记录 T 中字符出现次数和「窗口」中的相应字符的出现次数。
初始状态:
 {:align=center}
{:align=center}
增加 right,直到窗口 [left, right) 包含了 T 中所有字符:
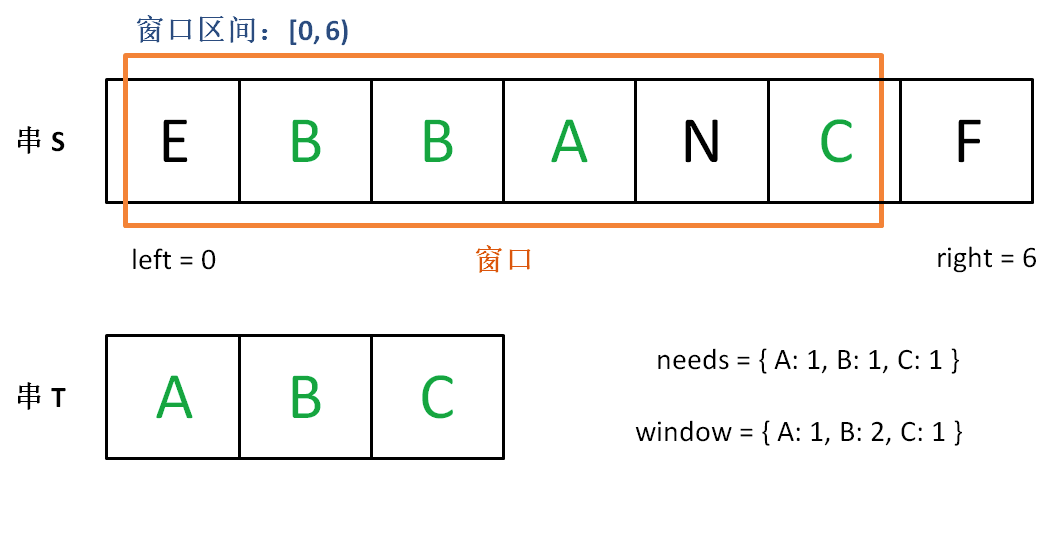 {:align=center}
{:align=center}
现在开始增加 left,缩小窗口 [left, right)。
 {:align=center}
{:align=center}
直到窗口中的字符串不再符合要求,left 不再继续移动。
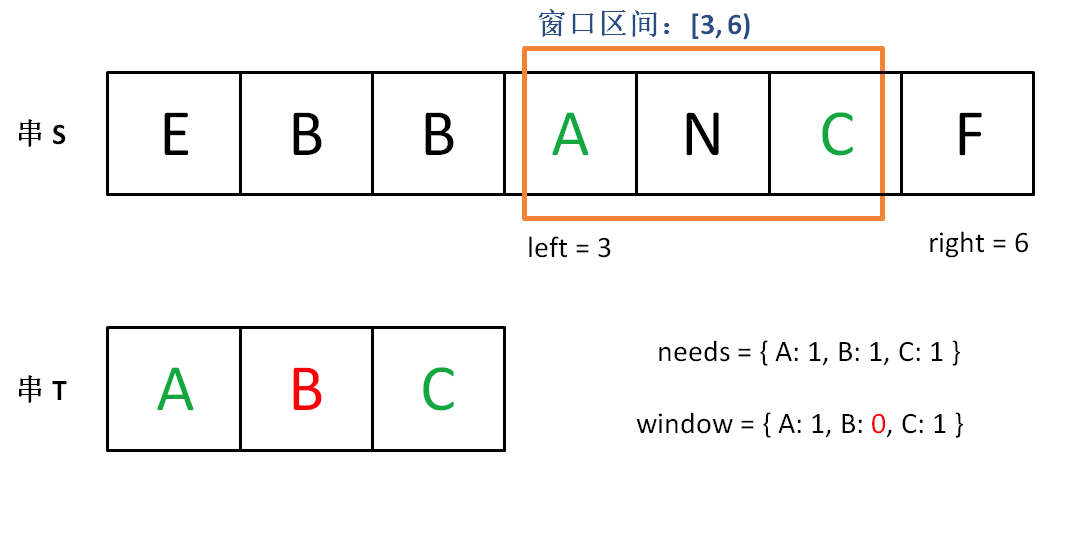 {:align=center}
{:align=center}
之后重复上述过程,先移动 right,再移动 left…… 直到 right 指针到达字符串 S 的末端,算法结束。
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。现在我们来看看这个滑动窗口代码框架怎么用:
首先,初始化 window 和 need 两个哈希表,记录窗口中的字符和需要凑齐的字符:
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
然后,使用 left 和 right 变量初始化窗口的两端,不要忘了,区间 [left, right) 是左闭右开的,所以初始情况下窗口没有包含任何元素:
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
// 开始滑动
}
其中 valid 变量表示窗口中满足 need 条件的字符个数,如果 valid 和 need.size 的大小相同,则说明窗口已满足条件,已经完全覆盖了串 T。
现在开始套模板,只需要思考以下四个问题:
1、当移动 right 扩大窗口,即加入字符时,应该更新哪些数据?
2、什么条件下,窗口应该暂停扩大,开始移动 left 缩小窗口?
3、当移动 left 缩小窗口,即移出字符时,应该更新哪些数据?
4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新?
如果一个字符进入窗口,应该增加 window 计数器;如果一个字符将移出窗口的时候,应该减少 window 计数器;当 valid 满足 need 时应该收缩窗口;应该在收缩窗口的时候更新最终结果。
下面是完整代码:
string minWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
// 记录最小覆盖子串的起始索引及长度
int start = 0, len = INT_MAX;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (valid == need.size()) {
// 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
// 返回最小覆盖子串
return len == INT_MAX ?
"" : s.substr(start, len);
}
需要注意的是,当我们发现某个字符在 window 的数量满足了 need 的需要,就要更新 valid,表示有一个字符已经满足要求。而且,你能发现,两次对窗口内数据的更新操作是完全对称的。
当 valid == need.size() 时,说明 T 中所有字符已经被覆盖,已经得到一个可行的覆盖子串,现在应该开始收缩窗口了,以便得到「最小覆盖子串」。
移动 left 收缩窗口时,窗口内的字符都是可行解,所以应该在收缩窗口的阶段进行最小覆盖子串的更新,以便从可行解中找到长度最短的最终结果。
至此,应该可以完全理解这套框架了,滑动窗口算法又不难,就是细节问题让人烦得很。以后遇到滑动窗口算法,你就按照这框架写代码,保准没有 bug,还省事儿。
下面就直接利用这套框架秒杀几道题吧,你基本上一眼就能看出思路了。
二、字符串排列
LeetCode 567 题,Permutation in String,难度 Medium:
 {:align=center}
{:align=center}
注意哦,输入的 s1 是可以包含重复字符的,所以这个题难度不小。
这种题目,是明显的滑动窗口算法,相当给你一个 S 和一个 T ,请问你 S 中是否存在一个子串,包含 T 中所有字符且不包含其他字符?
首先,先复制粘贴之前的算法框架代码,然后明确刚才提出的 4 个问题,即可写出这道题的答案:
// 判断 s 中是否存在 t 的排列
bool checkInclusion(string t, string s) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (right - left >= t.size()) {
// 在这里判断是否找到了合法的子串
if (valid == need.size())
return true;
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
// 未找到符合条件的子串
return false;
}
对于这道题的解法代码,基本上和最小覆盖子串一模一样,只需要改变两个地方:
1、本题移动 left 缩小窗口的时机是窗口大小大于 t.size() 时,应为排列嘛,显然长度应该是一样的。
2、当发现 valid == need.size() 时,就说明窗口中就是一个合法的排列,所以立即返回 true。
至于如何处理窗口的扩大和缩小,和最小覆盖子串完全相同。
三、找所有字母异位词
这是 LeetCode 第 438 题,Find All Anagrams in a String,难度 Medium:
 {:align=center}
{:align=center}
呵呵,这个所谓的字母异位词,不就是排列吗,搞个高端的说法就能糊弄人了吗?相当于,输入一个串 S ,一个串 T ,找到 S 中所有 T 的排列,返回它们的起始索引。
直接默写一下框架,明确刚才讲的 4 个问题,即可秒杀这道题:
vector<int> findAnagrams(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
vector<int> res; // 记录结果
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (right - left >= t.size()) {
// 当窗口符合条件时,把起始索引加入 res
if (valid == need.size())
res.push_back(left);
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
return res;
}
跟寻找字符串的排列一样,只是找到一个合法异位词(排列)之后将起始索引加入 res 即可。
四、最长无重复子串
这是 LeetCode 第 3 题,Longest Substring Without Repeating Characters,难度 Medium:
 {:align=center}
{:align=center}
这个题终于有了点新意,不是一套框架就出答案,不过反而更简单了,稍微改一改框架就行了:
int lengthOfLongestSubstring(string s) {
unordered_map<char, int> window;
int left = 0, right = 0;
int res = 0; // 记录结果
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
window[c]++;
// 判断左侧窗口是否要收缩
while (window[c] > 1) {
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
window[d]--;
}
// 在这里更新答案
res = max(res, right - left);
}
return res;
}
这就是变简单了,连 need 和 valid 都不需要,而且更新窗口内数据也只需要简单的更新计数器 window 即可。
当 window[c] 值大于 1 时,说明窗口中存在重复字符,不符合条件,就该移动 left 缩小窗口了嘛。
唯一需要注意的是,在哪里更新结果 res 呢?我们要的是最长无重复子串,哪一个阶段可以保证窗口中的字符串是没有重复的呢?
这里和之前不一样,要在收缩窗口完成后更新 res,因为窗口收缩的 while 条件是存在重复元素,换句话说收缩完成后一定保证窗口中没有重复嘛。
五、最后总结
建议背诵并默写这套框架,顺便背诵一下文章开头的那首诗。以后就再也不怕子串、子数组问题了好吧。
349. 两个数组的交集
力扣题目链接(opens new window)
题意:给定两个数组,编写一个函数来计算它们的交集。

说明: 输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序。
#算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** ::学透哈希表,set使用有技巧!Leetcode:349. 两个数组的交集 ****(opens new window)**** ,相信结合视频再看本篇题解,更有助于大家对本题的理解。
思路
这道题目,主要要学会使用一种哈希数据结构:unordered_set,这个数据结构可以解决很多类似的问题。
注意题目特意说明:输出结果中的每个元素一定是唯一的,也就是说输出的结果的去重的, 同时可以不考虑输出结果的顺序
这道题用暴力的解法时间复杂度是O(n^2),那来看看使用哈希法进一步优化。
那么用数组来做哈希表也是不错的选择,例如242. 有效的字母异位词(opens new window)
但是要注意,使用数组来做哈希的题目,是因为题目都限制了数值的大小。
而这道题目没有限制数值的大小,就无法使用数组来做哈希表了。
而且如果哈希值比较少、特别分散、跨度非常大,使用数组就造成空间的极大浪费。
此时就要使用另一种结构体了,set ,关于set,C++ 给提供了如下三种可用的数据结构:
- std::set
- std::multiset
- std::unordered_set
std::set和std::multiset底层实现都是红黑树,std::unordered_set的底层实现是哈希表, 使用unordered_set 读写效率是最高的,并不需要对数据进行排序,而且还不要让数据重复,所以选择unordered_set。
思路如图所示:
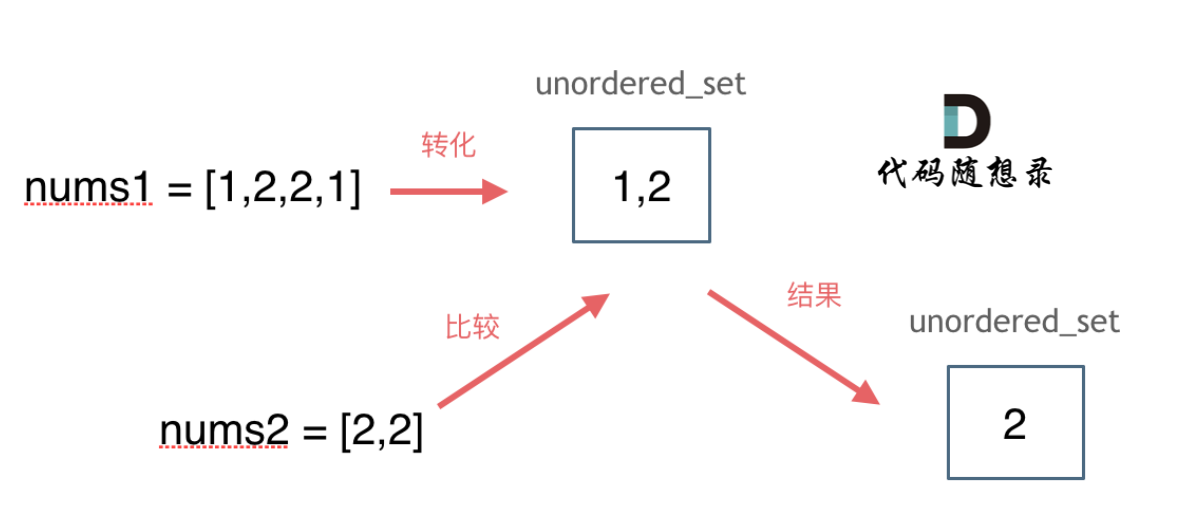
c++代码:
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; // 存放结果,之所以用set是为了给结果集去重
unordered_set<int> nums_set(nums1.begin(), nums1.end());
for (int num : nums2) {
// 发现nums2的元素 在nums_set里又出现过
if (nums_set.find(num) != nums_set.end()) {
result_set.insert(num);
}
}
return vector<int>(result_set.begin(), result_set.end());
}
拓展
那有同学可能问了,遇到哈希问题我直接都用set不就得了,用什么数组啊。
直接使用set 不仅占用空间比数组大,而且速度要比数组慢,set把数值映射到key上都要做hash计算的。
不要小瞧 这个耗时,在数据量大的情况,差距是很明显的。
用数组写的话:
class Solution{
public:
vector<int> intersection(vector<int>& nums1,vector<int>& nums2){
unordered_set<int> result_set;
int hash[1005] = {0};
for (int num : nums1){
hash[num] = 1;
}
for (int num : nums2){
if (hash[num] == 1){
result_set.insert(num);
}
}
return vector<int> (result_set.begin(),result_set.end());
}
};
第202题. 快乐数
力扣题目链接(opens new window)
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 True ;不是,则返回 False 。
示例:
输入:19
输出:true
解释:
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1
#思路
这道题目看上去貌似一道数学问题,其实并不是!
题目中说了会 无限循环,那么也就是说求和的过程中,sum会重复出现,这对解题很重要!
正如:关于哈希表,你该了解这些! **(opens new window)** 中所说,当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法了。
所以这道题目使用哈希法,来判断这个sum是否重复出现,如果重复了就是return false, 否则一直找到sum为1为止。
判断sum是否重复出现就可以使用unordered_set。
还有一个难点就是求和的过程,如果对取数值各个位上的单数操作不熟悉的话,做这道题也会比较艰难。
C++代码如下:
class Solution {
public:
// 取数值各个位上的单数之和
int getSum(int n) {
int sum = 0;
while (n) {
sum += (n % 10) * (n % 10);
n /= 10;
}
return sum;
}
bool isHappy(int n) {
unordered_set<int> set;
while(1) {
int sum = getSum(n);
if (sum == 1) {
return true;
}
// 如果这个sum曾经出现过,说明已经陷入了无限循环了,立刻return false
if (set.find(sum) != set.end()) {
return false;
} else {
set.insert(sum);
}
n = sum;
}
}
};
另外还有一种思路:
使用 “快慢指针” 思想,找出循环:“快指针” 每次走两步,“慢指针” 每次走一步,当二者相等时,即为一个循环周期。此时,判断是不是因为 1 引起的循环,是的话就是快乐数,否则不是快乐数。
注意:此题不建议用集合记录每次的计算结果来判断是否进入循环,因为这个集合可能大到无法存储;另外,也不建议使用递归,同理,如果递归层次较深,会直接导致调用栈崩溃。不要因为这个题目给出的整数是 int 型而投机取巧。
代码:
C++
class Solution {
public:
int bitSquareSum(int n) {
int sum = 0;
while(n > 0)
{
int bit = n % 10;
sum += bit * bit;
n = n / 10;
}
return sum;
}
bool isHappy(int n) {
int slow = n, fast = n;
do{
slow = bitSquareSum(slow);
fast = bitSquareSum(fast);
fast = bitSquareSum(fast);
}while(slow != fast);
return slow == 1;
}
};
这道题是第一道,我就不过多赘述了。直接呈现carl的代码随想录:
1. 两数之和
力扣题目链接(opens new window)
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
#算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** :梦开始的地方,Leetcode:1.两数之和 ****(opens new window)**** ,相信结合视频再看本篇题解,更有助于大家对本题的理解。
#思路
很明显暴力的解法是两层for循环查找,时间复杂度是O(n^2)。
建议大家做这道题目之前,先做一下这两道
- 242. 有效的字母异位词(opens new window)
- 349. 两个数组的交集(opens new window)
242. 有效的字母异位词 **(opens new window)** 这道题目是用数组作为哈希表来解决哈希问题,349. 两个数组的交集 **(opens new window)** 这道题目是通过set作为哈希表来解决哈希问题。
首先我再强调一下 什么时候使用哈希法,当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
本题呢,我就需要一个集合来存放我们遍历过的元素,然后在遍历数组的时候去询问这个集合,某元素是否遍历过,也就是 是否出现在这个集合。
那么我们就应该想到使用哈希法了。
因为本题,我们不仅要知道元素有没有遍历过,还要知道这个元素对应的下标,需要使用 key value结构来存放,key来存元素,value来存下标,那么使用map正合适。
再来看一下使用数组和set来做哈希法的局限。
- 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
- set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
此时就要选择另一种数据结构:map ,map是一种key value的存储结构,可以用key保存数值,用value再保存数值所在的下标。
C++中map,有三种类型:
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(log n) | O(log n) |
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(log n) | O(log n) |
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。
同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。 更多哈希表的理论知识请看关于哈希表,你该了解这些! **(opens new window)** 。
这道题目中并不需要key有序,选择std::unordered_map 效率更高! 使用其他语言的录友注意了解一下自己所用语言的数据结构就行。
接下来需要明确两点:
- map用来做什么
- map中key和value分别表示什么
map目的用来存放我们访问过的元素,因为遍历数组的时候,需要记录我们之前遍历过哪些元素和对应的下标,这样才能找到与当前元素相匹配的(也就是相加等于target)
接下来是map中key和value分别表示什么。
这道题 我们需要 给出一个元素,判断这个元素是否出现过,如果出现过,返回这个元素的下标。
那么判断元素是否出现,这个元素就要作为key,所以数组中的元素作为key,有key对应的就是value,value用来存下标。
所以 map中的存储结构为 {key:数据元素,value:数组元素对应的下标}。
在遍历数组的时候,只需要向map去查询是否有和目前遍历元素匹配的数值,如果有,就找到的匹配对,如果没有,就把目前遍历的元素放进map中,因为map存放的就是我们访问过的元素。
过程如下:
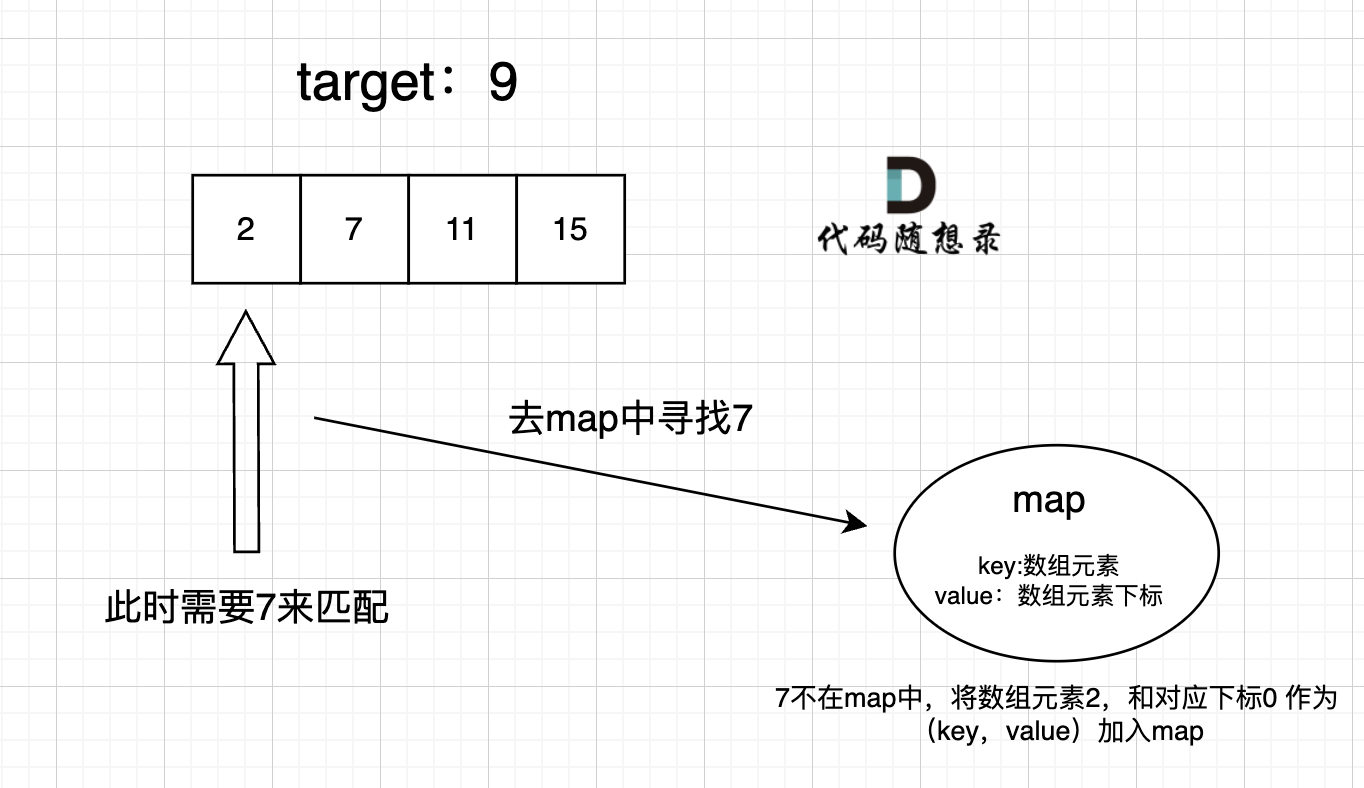
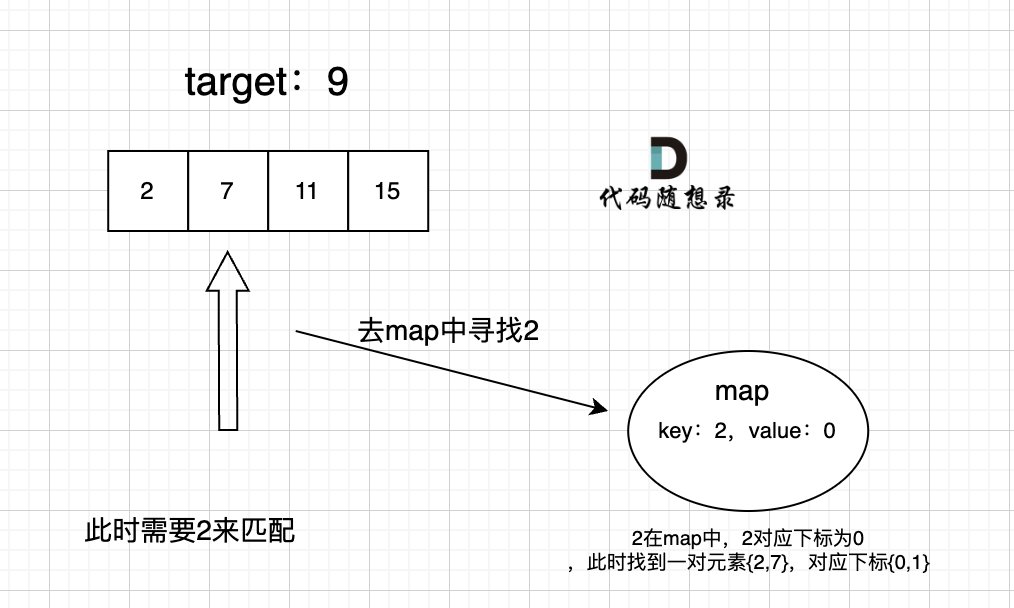
C++代码:
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
std::unordered_map <int,int> map;
for(int i = 0; i < nums.size(); i++) {
// 遍历当前元素,并在map中寻找是否有匹配的key
auto iter = map.find(target - nums[i]);
if(iter != map.end()) {
return {iter->second, i};
}
// 如果没找到匹配对,就把访问过的元素和下标加入到map中
map.insert(pair<int, int>(nums[i], i));
}
return {};
}
};
-
时间复杂度: O(n)
-
空间复杂度: O(n)
class Solution { public: vector<int> twoSum(vector<int>& nums, int target) { unordered_map<int,int> heap; for (int i = 0;i < nums.size() ;i++){ int r = target - nums[i]; if (heap.count(r) )return {heap[r],i}; heap[nums[i]] = i; } return {}; } };
#总结
本题其实有四个重点:
- 为什么会想到用哈希表
- 哈希表为什么用map
- 本题map是用来存什么的
- map中的key和value用来存什么的
把这四点想清楚了,本题才算是理解透彻了。
很多录友把这道题目 通过了,但都没想清楚map是用来做什么的,以至于对代码的理解其实是 一知半解的。