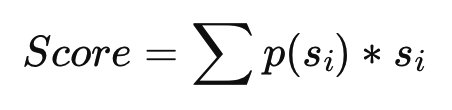引子

例如，现在需要拟合函数f(x)，我们已知函数上的若干点（xi，yi）

现在我们想知道在自变量取x’的时候，函数值y’为多少

正常的思路比如拉格朗日插值，牛顿插值，直接去估计函数的表达式，然后带入点值去计算y’

但是根据数学直觉来说，函数如果是连续的，那么离查询点x’越近的点xi，会对y’造成的影响越大

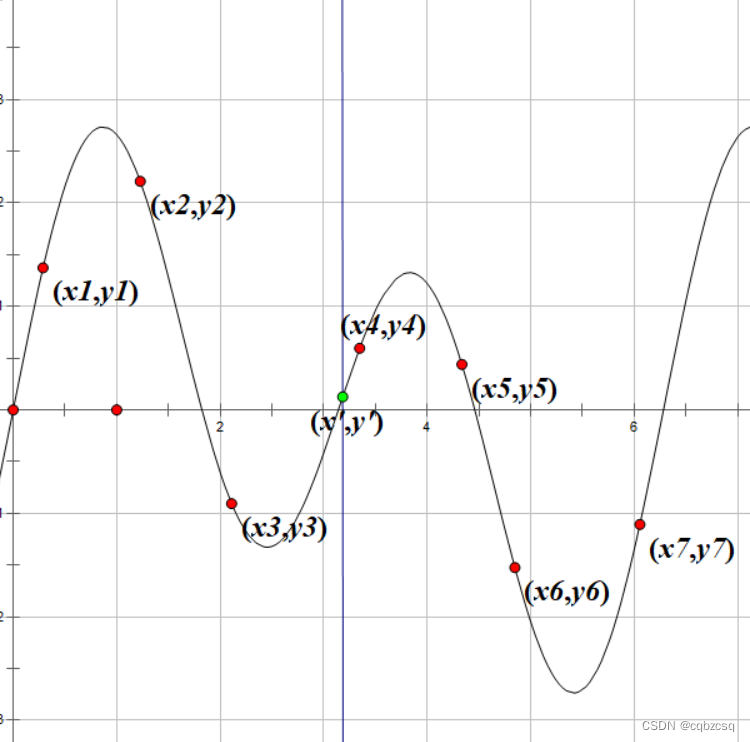
如上图，（x4，y4）对需要查询的(x',y')带来的影响相比于(x7,y7)显然是更大的

如果说我们假设目前的函数模型是一个简单的求平均值模型即

根据我们上文的发现，我们可以把它改写为加权平均值

   ，满足 

然后我们来使用神经网络训练这个加权的权重，输入两个变量(x,xi)，输出为权重

当然还要满足，这一点可以用喜闻乐见的softmax函数来实现

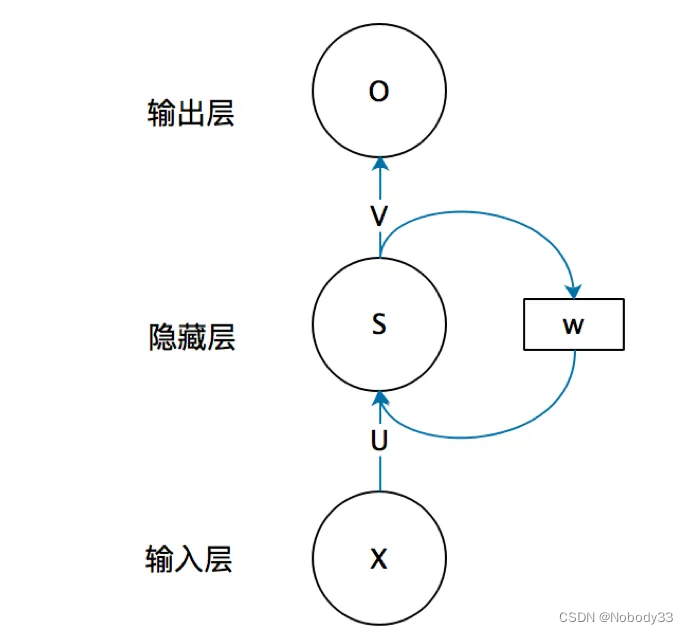
根据上述这种做法（似乎也被称为Nadaraya-Watson核回归），我们抽象出注意力机制的基本模型

注意力机制

查询Q、键K、值V

老生常谈的内容了

查询Q就相当于我们输入进入函数的那个x’

键K就是我们已知函数点的x坐标

值V就是我们已知函数点的y坐标

我们的输出就是一系列V的加权和

现在的重点就是如何设计这个函数，也就是注意力评分函数，能够让拟合效果尽量好

有两种主流的设计方法（当然还有很多其他的方法）

假设我们输入为q向量和k向量

加性注意力：

在pytorch中可以利用tensor加法的广播机制来做到矩阵化运算

缩放点积注意力：(要求q与k向量长度相同，均为d)

这个形式直接可以写成矩阵乘法的形式，在套上一个softmax就算完了，所以比较受大众喜爱

为了能够更好地使用这种机制（为了把更多的死马当作活马医）

我们添加全连接层，例如网络中的某个阶段，特征为X

我们给它加三个分别的全连接层Qx，Kx，Vx，得到QKV矩阵，就能够用上述的注意力模型套了

然后美其名曰，自注意力机制（我实在没想通这样做到底有什么意义，或许是构造了二阶特征？）

事实证明，这个机制确实发挥了非常巨大的作用（你就说它行不行吧）

说到注意力那就必须得提起Transformer

Transformer里面使用的注意力机制更加优秀，虽然仍然使用的seq2seq架构

他利用了上文的context作为解码器输入的Q和K，解码器两层注意力，第一层是自注意力，第二层是自身作为V的输入，利用上文context作为Q、K的输入，融合到一起的注意力层（更有使用查询和键、值的实际意义）（但为什么是作为Q、K，而不是只作为Q呢？），另外他还设计了非常巧妙的位置编码，减少了位置信息的损失。

不过这里并不打算展开讲

推荐一个非常优质的、图文并茂的Transformer的讲解。

The Illustrated Transformer – Jay Alammar – Visualizing machine learning one concept at a time.