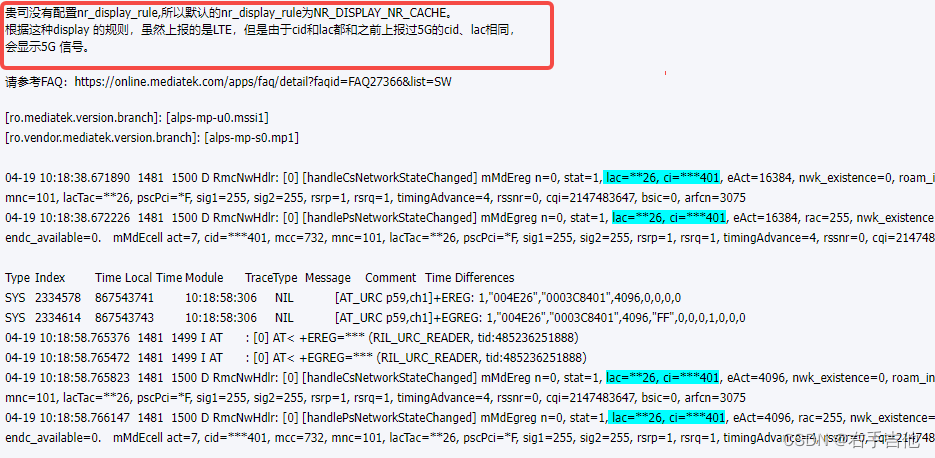
题目描述：

写一个函数,输入n,求斐波那契数列的第n项.斐波那契数列定义如下:

F(0) = 0
F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

解题方法：

算法1:

利用递归实现,这个方法效率有严重问题,时间复杂度为O(2^n)

long long Fibon(int n)
{
    if (n < 2)
        return n;
    return Fibon(n - 2) + Fibon(n - 1);
}

int main()
{
    for (int i = 1; i < 10; i++)//这个测试没有问题
        printf("%lld ",Fibon(i));

    printf("%lld\n",Fibon(50));//递归函数执行速度非常慢

    return 0;
}

算法2:

利用动态规划,循环实现.O(n),O(1)

long long Fibon(int n)
{
    long long f1 = 1; //第一项数据
    long long f2 = 1; //第二项数据
    long long f3 = 1; //当前项数据
    for (int i = 3; i <= n; i++)
    {
        f3 = f1 + f2;//当前项=前两项之和
        f1 = f2;//f1递推为后一项的值
        f2 = f3;//f2递推为后一项的值
    }
    return f3;
}

int main()
{
    for (int i = 1; i < 10; i++)//这个测试没有问题
        printf("%lld ",Fibon(i));
    printf("\n");
    printf("%lld\n",Fibon(50));//递归函数执行速度非常慢

    return 0;
}

算法3:

利用数学矩阵公式求解.O(logn)

这个公式比较生僻,大家了解一下.

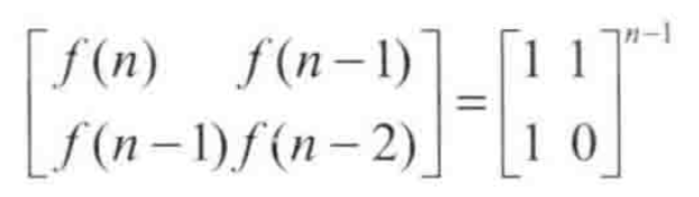
//这个算法难度较大,仅做参考
long long* Multi(long long* arr, int n)
{
    long long* brr = (long long*)malloc(4 * sizeof(long long));
    if (brr == NULL) return NULL;
    brr[0] = brr[1] = brr[2] = 1;
    brr[3] = 0;
    if (n == -1) {
        brr[0] = 0;
        return brr;
    }
    else if (n == 0 || n==1)
        return brr;
    long long* crr = Multi(arr, n / 2);
    //计算crr*crr
    brr[0] = crr[0] * crr[0] + crr[1] * crr[2];
    brr[1] = crr[0] * crr[1] + crr[1] * crr[3];
    brr[2] = crr[2] * crr[0] + crr[3] * crr[2];
    brr[3] = crr[2] * crr[1] + crr[3] * crr[3];
    if (n % 2 != 0)//奇数,brr = brr*arr
    {
        crr[0] = brr[0] * arr[0] + brr[1] * arr[2];
        crr[1] = brr[0] * arr[1] + brr[1] * arr[3];
        crr[2] = brr[2] * arr[0] + brr[3] * arr[2];
        crr[3] = brr[2] * arr[1] + brr[3] * arr[3];
        brr[0] = crr[0];
        brr[1] = crr[1];
        brr[2] = crr[2];
        brr[3] = crr[3];
    }
    free(crr);
    return brr;
}

int Fibon(int n){
    long long arr[] = {1,1,1,0};
    long long* p = Multi(arr,n-1);
    int tmp = p[0];
    free(p);
    return tmp;
}
int main()
{
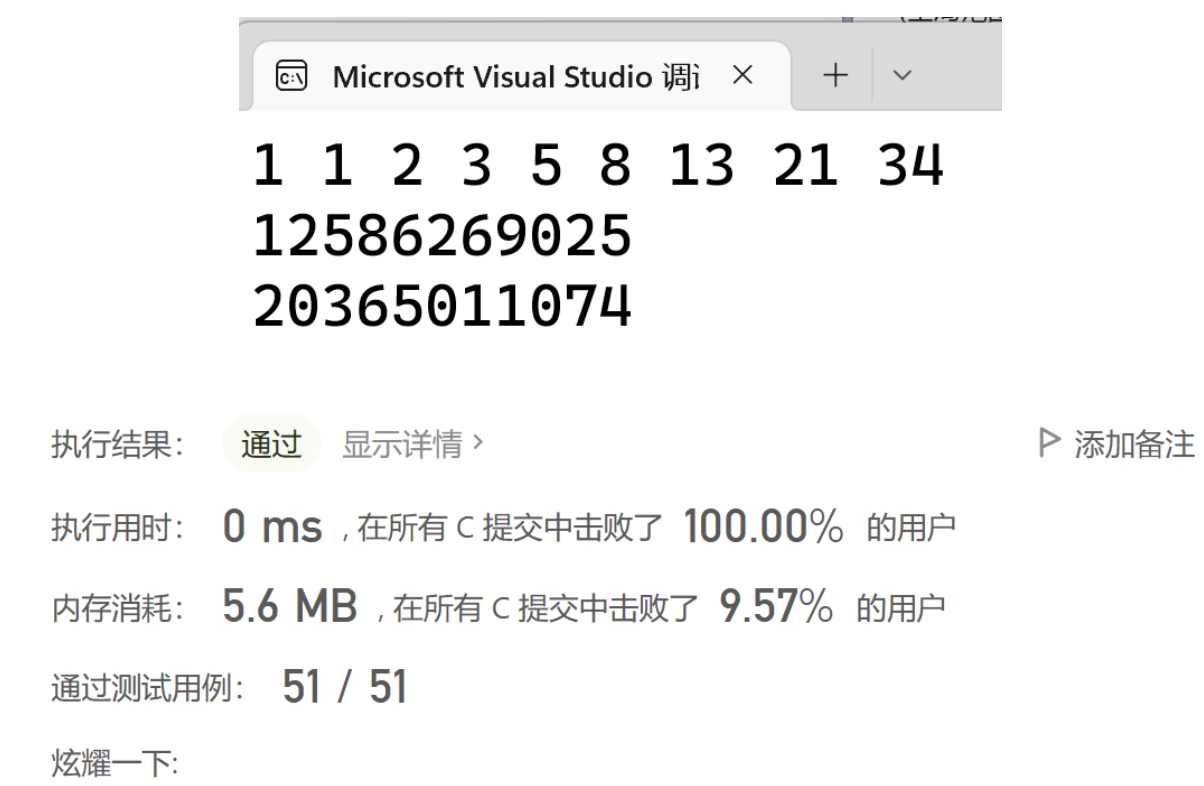
    for (int i = 1; i < 10; i++)
        printf("%lld ",Fibon(i));
    printf("\n");
    printf("%lld\n",Fibon(50));
    printf("%lld\n", Fibon(51));

    return 0;
}