哈夫曼编码是一种无损数据压缩算法，该算法在数据压缩，存储和网络传输等领域广泛引用，对互联网的发展也产生了深远的影响。
大家熟知的数据无损压缩软件，如WinRAR，gzip，bzip，lzw，7-zip等，都应用了哈夫曼算法。
广泛使用的PNG，JPEG，WebP图像格式，MP3音频格式，H.264(AVC)和H.265(HEVC)视频编码标准，都应用了哈夫曼编码。
1. 在传递信息时，如何尽量节省空间并保证无损编译？
如果要用01编码向某向某人传递信息，并要求尽可能节省空间且数据无损坏，要如何进行设计与实现？
我们已经了解过ASCLL这种编码方式了，对于每一种字符，我们用等长的八位二进制编码对其进行表示。
但是，当我们需要用到的字符较少时，每个字符都使用八位二进制来进行编码就会浪费很多空间。
那么，我们要如何设计一种编码方式来针对特定的情况进行编码呢？
1.1 等长编码
假设我们要传递的信息是单词“success”。
我们的第一种思路依然是采用等长的二进制序列来进行编码，但是，针对特定情况，我们可以采用较少的二进制位来编码。
对具体情况进行分析，我们发现，success中只有四种字符（s，u，c，e），于是我们只需要用2位二进制便可编码：
| 字符 | s | u | c | e |
| 编码 | 00 | 01 | 10 | 11 |
依据此编码方式，我们可以将success转化为二进制序列“00011010110000”。
在解码时，只需对照编码表，每二位一译即可无损译出“success”。
该种编码方式，相对于用ASCLL码来编译节省了许多的空间，并且做到了无损译码。
但是，还能节省更多空间吗？
1.2 变长编码
在刚才的例子中，我们经过思考我们找到一种思路：出现频率高的字符，采用较短的编码。
简单分析会发现，success中，s出现了3次，c出现了2次，e和u各一次。
于是我们可以采用以下这种编码方式：
| 字符 | s | c | e | u |
| 编码 | 0 | 1 | 01 | 11 |
依据此编码方式，我们可以将success转化为二进制序列“011110100”。
相比于刚才总长14位的二进制编码，这次我们仅用了9位二进制就表示出了“success”，压缩率达到64%。
但是，变长编码在解决长度问题的同时，又导致无损编码成为了问题。
例如，在解码的过程中，我们可以有这些不同的方式来理解所接收到的信息：
011110100 ------> eucess
011110100 ------> suuess
……
也就是说，我们的编码具有不确定性，数据没有完好无损地被接收到。
反思我们设计出的编码，会发现导致二进制序列的解码出现不确定性的原因是，某些字符的编码是另外一些字符的前缀。
我们在解读时，无法分辨该位二进制位是用于单独表示一个字符，还是与其后的二进制位结合以表示另一个字符。
1.3 前缀码
根据以上案例的分析，我们总结出以下要点：
1. 整体上要采用变长编码，出现频次多的字符用短码。
2. 任一编码不能是另一编码的前缀。
只要保证以上两点，我们就可以解决编码尽量短且无损编译的问题。
但是，如何确保第二点的成立呢？
假如我们定义“s”的编码为“0”，那么，接下来所有的字符的编码都不能以“0”作为开头。
同时，不能将“1”单独作为另一字符的编码，因为这样就会导致“0”和“1”都不能作为开头。
以此类推，第二位，第三位……都是如此。
也就是说，每确定一个字符的编码，接下来的字符的编码的长度就会比上一个多1。
这样的编码规则和规律使得我们联想到树的结构，我们可以利用树来直观表示这个过程。
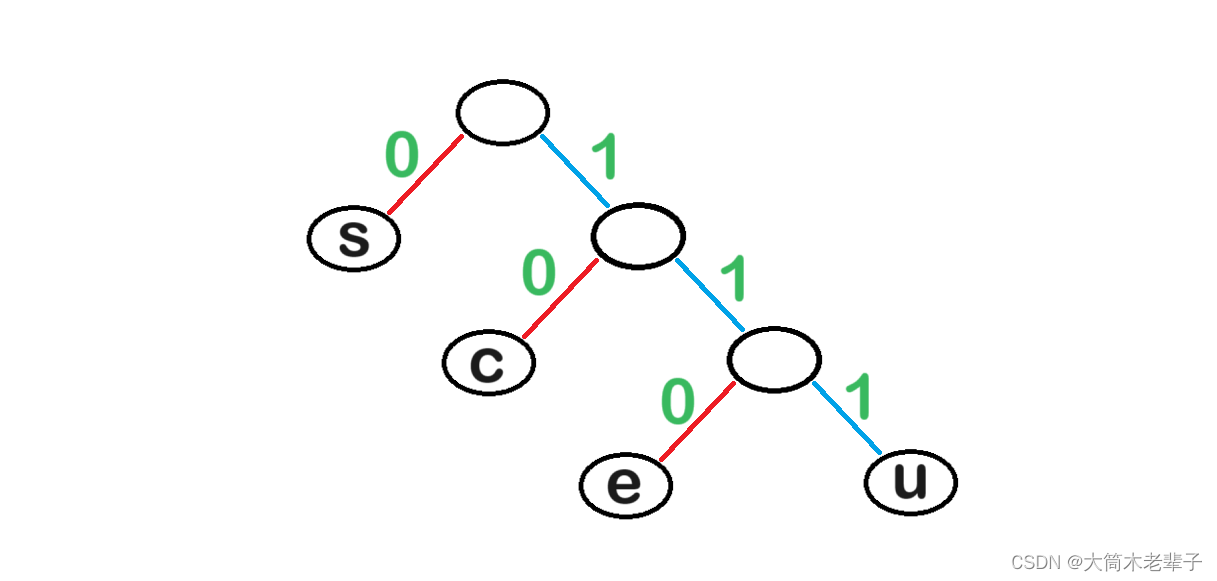
于是，我们可以得到以下的编码表：
| 字符 | s | c | e | u |
| 编码 | 0 | 10 | 110 | 111 |
依据此编码方式，我们可以将success转化为二进制序列“0111101011000”。
共十三位二进制，尽管压缩率相比于之前有所下降，但是却能保证无损编译。
1.4 总结
1. 整体上要采用变长编码，出现频次多的字符用短码。
2. 通过树来帮助我们编码，就可以保证某个字符的编码不是另一个字符编码的前缀。
3. 往树的左子树表示编码增加一个“0”，往树的右子树表示编码增加一个“1”（也可交换）。
4. 树的叶子节点表示一个字符，从根结点到叶子结点的路径就是该字符的编码。
但问题是，即使按照以上的方式来编码，依然有很多可能的编码方式（树的形状）能供我们选择。
既然都研究到这里了，我们肯定不会随机选择一个。
所以接下来，我们就继续研究，如何确定哪棵树是最优的，或者说，如何生成最优的树。
2. 香农-范诺编码
1. 字符按出现的频次降序排列。
2. 二分法找出一个分界点，使得左边的总频次和右边的总频次尽可能相近。
3. 左半边分配编码“0”， 右半边分配编码“1”。
4. 递归二分法，直到每个字符都成为编码树的叶子节点。
香农是信息论的创立者，范诺是麻省理工大学的教授，二者共同提出的建立最优树的方式就被称作“香农-范诺编码”。
这种建立最优树的方式的思路很好理解：
我们刚才已经分析过，如果确定了某个字符的编码的长度，之后所有字符的编码的长度都一定会比这个字符的编码长。
所以，我们尝试让树的两边尽可能地平均，就像上一张图中的第三棵树一样。
从图中可以直观地看出，这样做可以使得特别长的编码尽可能地少出现，编码长度的分配在整体上变得较为平均。
当然，整体上依然要保持出现频次较高地字符使用更短的编码。
所以，按照“香农-范诺编码”的规则创建出来的树也不一定是两边分配十分平均的。
还是我们之前用到的success的例子，按照上面的规则，创建出来的树的形状为：
可以验证，在这个例子下，这棵树确实是最优解。
但是，对于其他情况依然适用吗？要如何证明呢？
我不知道，因为这也是这两位大佬所面临的问题---无法证明这样构建出来的树一定是最优的那棵。
3. 哈夫曼编码
3.1 背景
“如何构建最佳前缀码？”
这是1951年麻省理工学院（MIT）信息论课程，给学生布置的课程报告题目。
负责该课程的教授，就是范诺（Robert M.Fano），而哈夫曼，正是范诺的学生。
哈夫曼和他在MIT的同学面临完成课程报告或期末考试获得课程学分的抉择。
哈夫曼选择了课程报告，而范诺教授并没有告诉自己的学生，这其实是自己正在研究而为解决的课题。
哈夫曼一开始的思路是想改进导师的算法，花费了数月的时间，研究了多种方法，但没有一种方法可以证明是最有效的。
正当他准备放弃时，突然灵光一现，发明了自下而上构建前缀码的方法，也就是哈夫曼编码。（香农-范诺编码采用的是自上而下构建方式）
3.2 哈夫曼树
可证明是带权路径长度最短的二叉树（最优二叉树）。
带权路径长度WPL（Weighted Path Length）= 树根到叶子结点的路径长度 * 叶子结点的权
树的带权路径长度为书中所有叶子结点的带权路径长度之和，通常记为
叶子结点的权也就是叶子结点的权重，在这里指叶子结点代表的字符的出现频次。
也就是说，最优二叉树就是带权路径长度最短的二叉树。
3.2.1 哈夫曼树的构造方式
原则：
1. 权值越大的叶结点越靠近根结点。
2. 权值越小的叶结点越远离根结点。
步骤：
1. 构造n棵只含根结点的二叉树。
2. 在森林中选取两棵根结点权值最小的树作为左右子树，构造一棵新的二叉树，新的根结点 权值为其左右子树根结点的权值之和。
3. 在森林中删除这两棵树，同时将新得到的二叉树加入到森林中。
4. 重复2，3步，直到森林中只含一棵树为止，这棵树就是哈夫曼树。
采用这种方式构建出来的二叉树也不一定是唯一的，但这些不唯一的树一定都是等效的。
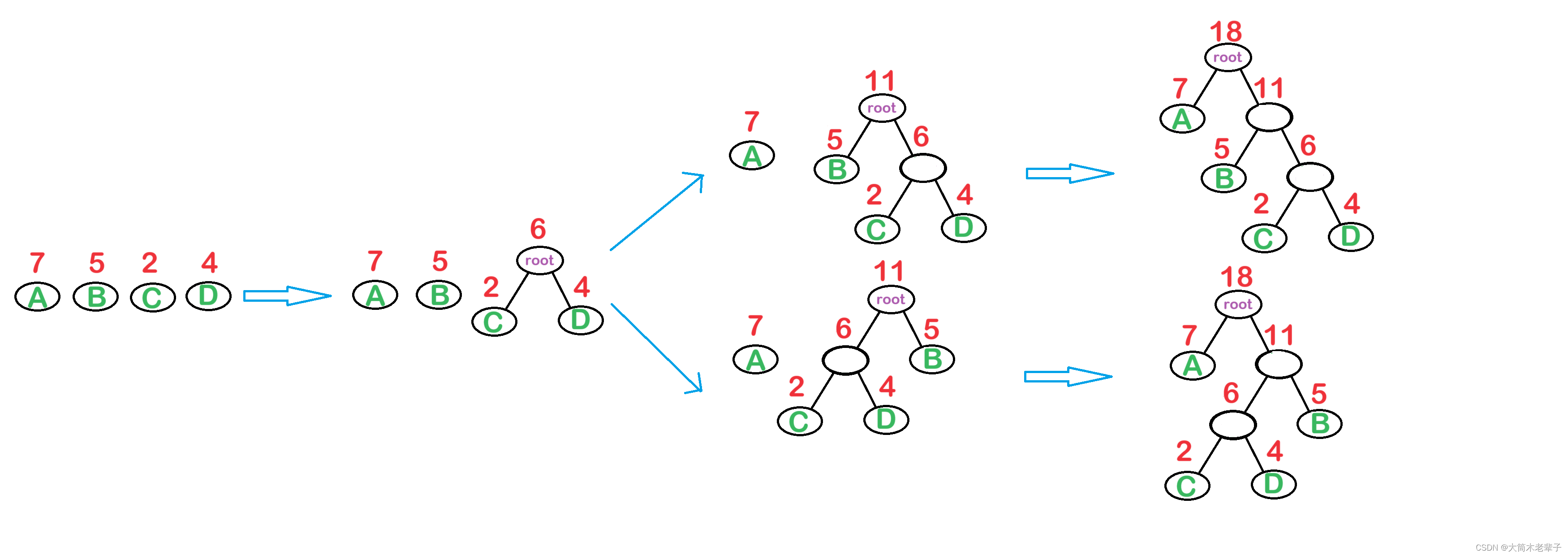WPL = 7 * 1 + 4 * 3 + 2 * 3 + 5 * 2 = 35。
3.2.2 规范哈夫曼树的构造算法
由于哈夫曼树并不唯一，所以，为了使用的方便与统一，我们在写代码实现的时候需要尽量保证生成的哈夫曼树唯一。
设当前森林为：F = {T1，T2，……，Tn}，构造时的选择规范为：
1. 权值小的二叉树作为新构造的二叉树的左子树。
2. 权值大的二叉树作为新构造的二叉树的右子树。
3. 在权值相等时：
深度小的二叉树作为新构造的二叉树的左子树。
深度大的二叉树作为新构造的二叉树的右子树。
那么，我们的哈夫曼树是采用链式存储结构还是顺序存储结构？
3.2.3 顺序存储结构的哈夫曼树
树的结构定义：
typedef struct TreeNode
{
char data;//数据---对应的字符
int weight;//权值
int parent;//父结点
int lchild;//左孩子
int rchild;//右孩子
}HTNode;//当不存在父结点或左右孩子时，对应值为-1构造哈夫曼树：
//构造哈夫曼树
void CreatHT(HTNode ht[], int n)
{
int i, k, lnode, ronde;
double min1, min2;
for(i = 0; i < 2 * n - 1; i++)//将所有结点初始化, 含n个叶子结点的二叉树共有2*n-1个结点
{
ht[i].parent = ht[i].lchild = ht[i].rchild = -1;
}
for(i = n; i < 2 * n - 1; i++)//前n个结点为叶子结点, 下标从n到2*n-2的结点都是新产生的结点
{
min1 = min2 = 32767;//任意大数，需确保比2*n-1大
lnode = rnode = -1;
for(k = 0; k <= i - 1; k++)//遍历已有结点
{
if(ht[k].parent == -1)//父结点不为-1的视为已被销毁
{
if(ht[k].weight <= min1)//找权值最小的两个结点，同时保证min1(对应左子树lnode)较小
{
min2 = min1;
rnode = lnode;
min1 = ht[k].weight;
lnode = k;
}
else if(ht[k].weight <= min2)
{
min2 = ht[k].weight;
rnode = k;
}
}
}
ht[i].weight = ht[lnode].weight + ht[rnode].weight;
ht[i].lchild = lnode;
ht[i].rchild = rnode;
ht[lnode].parent = i;
ht[rnode].parent = i;
}
}在调用之前，需要先创建好有m=2*n-1个结点元素的数组，并将前n个结点元素对应的符号（不必须）以及权值（必须）初始化好。
获取编码本：
//编码本
#define LEN 100 //待编码字符个数
typedef struct
{
char ch; //存储字符
char code[LEN]; //存放编码(编码长度不会超过字符个数)
}TCode;
TCode CodeBook[LEN]; //编码本
//获得编码本
void encoding(HTNode ht[], TCode book[], int n)
{
char* str = (char*)malloc(n + 1);
str[n] = '\0';
int i, j, idx, p;
for(i = 0; i < n; i++)//遍历编码本
{
book[i].ch = ht[i].ch;
idx = i;
j = n;
while(p = ht[idx].parent > 0)//由底至上访问树，从后向前生成编码
{
if(ht[p].lchild == idx)
{
j--;
str[j] = '0';
}
else
{
j--;
str[j] = '1';
}
idx = p;
}
strcpy(book[i].code, &str[j]);
}
}获取到的编码本用于展示给用户作为参考，解码的过程直接在树上对编码进行解读即可。
解码算法：
//哈夫曼解码算法
void decoding(HTNode ht[], char* codes, int n)
{
int i, p;
i = 0;
p = 2 * n - 2;
while(codes[i] != '\0')
{
while(ht[p].lchild != -1 && ht[p].rchild != -1)
{
if(codes[i] == '0')
p = ht[p].lchild;
else
p = ht[p].rchild;
i++;
}
printf("%c", ht[p].ch);
p = 2 * n - 2;
}
printf("\n");
}3.2.4 链式存储结构的哈夫曼树
懒得写了，改天再写。
