零、回溯算法理论
参考链接13.1 回溯算法 - Hello 算法 (hello-algo.com)
1.尝试与回退
之所以称之为回溯算法,是因为该算法在搜索解空间时会采用“尝试”与“回退”的策略。当算法在搜索过程中遇到某个状态无法继续前进或无法得到满足条件的解时,它会撤销上一步的选择,退回到之前的状态,并尝试其他可能的选择。
例题1:在二叉树中搜索所有值为 7 的节点,请返回根节点到这些节点的路径。
/* 前序遍历:例题二 */
void preOrder(TreeNode root) {
if (root == null) {
return;
}
// 尝试
path.add(root);
if (root.val == 7) {
// 记录解
res.add(new ArrayList<>(path));
}
preOrder(root.left);
preOrder(root.right);
// 回退
path.remove(path.size() - 1);
}
在每次“尝试”中,我们通过将当前节点添加进 path 来记录路径;而在“回退”前,我们需要将该节点从 path 中弹出,以恢复本次尝试之前的状态。
注意感受回溯对path的影响
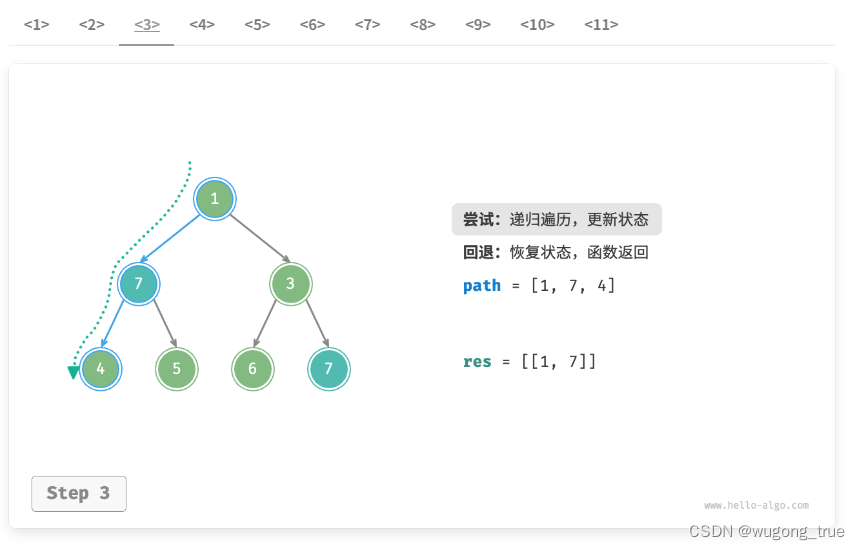
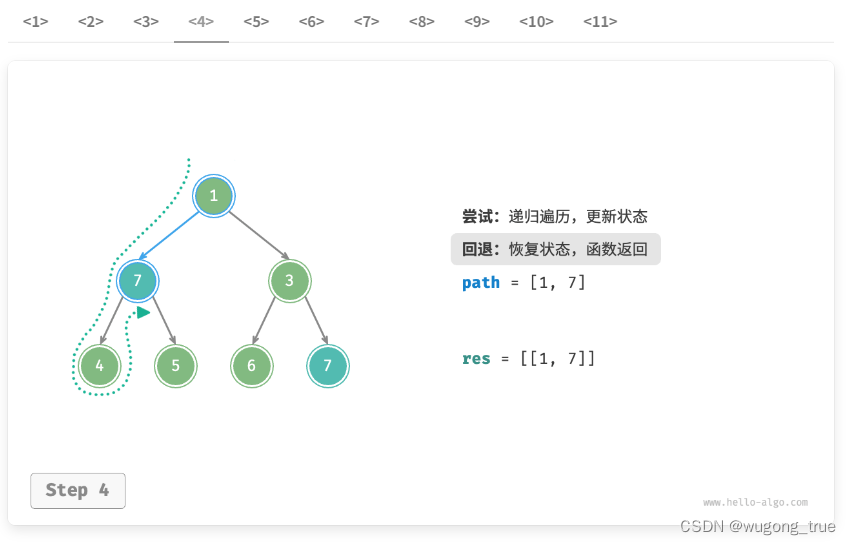
2.剪枝
复杂的回溯问题通常包含一个或多个约束条件,约束条件通常可用于“剪枝”
例题2:在二叉树中搜索所有值为 7 的节点,请返回根节点到这些节点的路径,并要求路径中不包含值为 3 的节点。
/* 前序遍历:例题三 */
void preOrder(TreeNode root) {
// 剪枝
if (root == null || root.val == 3) {
return;
}
// 尝试
path.add(root);
if (root.val == 7) {
// 记录解
res.add(new ArrayList<>(path));
}
preOrder(root.left);
preOrder(root.right);
// 回退
path.remove(path.size() - 1);
}
“剪枝”是一个非常形象的名词。在搜索过程中,**我们“剪掉”乐不满足约束条件的搜索分支,**避免许多无意义的尝试,从而提高了搜索效率。
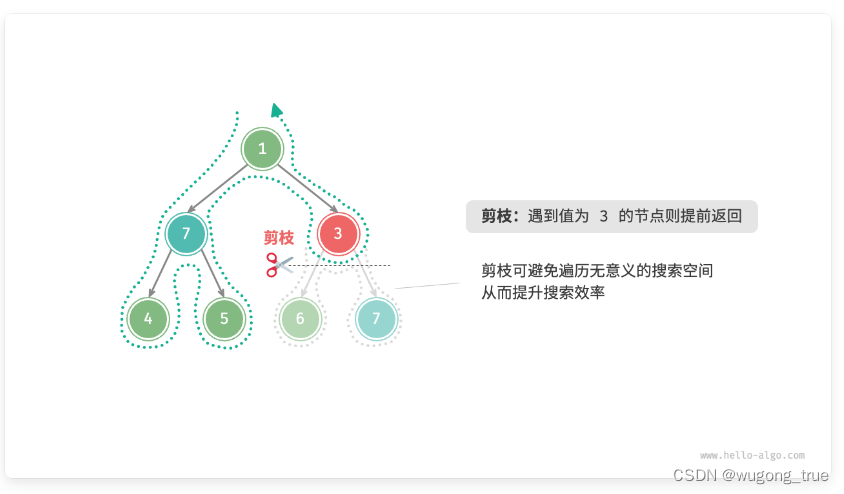
3.框架代码
将主体框架提炼出来,提升代码的通用性:
- 尝试
- 回退
- 剪枝
框架
/* 回溯算法框架 */
void backtrack(State state, List<Choice> choices, List<State> res) {
// 判断是否为解
if (isSolution(state)) {
// 记录解
recordSolution(state, res);
// 不再继续搜索
return;
}
// 遍历所有选择
for (Choice choice : choices) {
// 剪枝:判断选择是否合法
if (isValid(state, choice)) {
// 尝试:做出选择,更新状态
makeChoice(state, choice);
backtrack(state, choices, res);
// 回退:撤销选择,恢复到之前的状态
undoChoice(state, choice);
}
}
}
4.常用术语
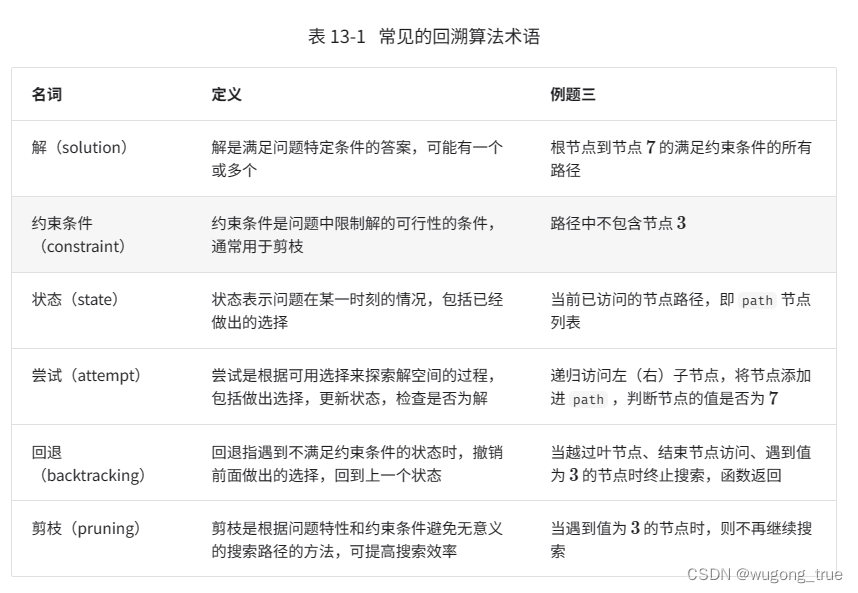
在框架基础上解决例题2
5.优点和局限性
回溯算法的本质是深度优先搜索算法,它尝试所有可能的解决方案直到找到满足条件的解。
优点:
能够找到所有可能的解决方案,并且在合理的剪枝操作下,具有很高的效率
缺点:
在处理大规模或者复杂问题时,回溯算法的运行效率可能难以接受
- 时间:回溯算法通常需要遍历状态空间的所有可能,时间复杂度可以达到指数阶或阶乘阶。
- 空间:在递归调用中需要保存当前的状态(例如路径、用于剪枝的辅助变量等),当深度很大时,空间需求可能会变得很大。
即便如此,回溯算法仍然是某些搜索问题和约束满足问题的最佳解决方案。(有些问题目前来讲只能由回溯算法解决)。关键是如何优化效率
- 剪枝:避免搜索那些肯定不会产生解的路径,从而节省时间和空间。
- 启发式搜索:在搜索过程中引入一些策略或者估计值,从而优先搜索最有可能产生有效解的路径。
6.回溯典型例题
搜索问题:这类问题的目标是找到满足特定条件的解决方案。
- 全排列问题:给定一个集合,求出其所有可能的排列组合。
- 子集和问题:给定一个集合和一个目标和,找到集合中所有和为目标和的子集。
- 汉诺塔问题:给定三根柱子和一系列大小不同的圆盘,要求将所有圆盘从一根柱子移动到另一根柱子,每次只能移动一个圆盘,且不能将大圆盘放在小圆盘上。
约束满足问题:这类问题的目标是找到满足所有约束条件的解。
- 𝑛 皇后:在 𝑛×𝑛 的棋盘上放置 𝑛 个皇后,使得它们互不攻击。
- 数独:在 9×9 的网格中填入数字 1 ~ 9 ,使得每行、每列和每个 3×3 子网格中的数字不重复。
- 图着色问题:给定一个无向图,用最少的颜色给图的每个顶点着色,使得相邻顶点颜色不同。
组合优化问题:这类问题的目标是在一个组合空间中找到满足某些条件的最优解。
- 0-1 背包问题:给定一组物品和一个背包,每个物品有一定的价值和重量,要求在背包容量限制内,选择物品使得总价值最大。
- 旅行商问题:在一个图中,从一个点出发,访问所有其他点恰好一次后返回起点,求最短路径。
- 最大团问题:给定一个无向图,找到最大的完全子图,即子图中的任意两个顶点之间都有边相连。
请注意,对于许多组合优化问题,回溯不是最优解决方案。
- 0-1 背包问题通常使用动态规划解决,以达到更高的时间效率。
- 旅行商是一个著名的 NP-Hard 问题,常用解法有遗传算法和蚁群算法等。
- 最大团问题是图论中的一个经典问题,可用贪心算法等启发式算法来解决。
电话号码的字母组合
参考链接17. 电话号码的字母组合 - 力扣(LeetCode)
class Solution {
//一个映射表,第二个位置是"abc“,第三个位置是"def"。。。
//这里也可以用map,用数组可以更节省点内存
String[] letter_map = {" ","*","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public List<String> letterCombinations(String digits) {
//注意边界条件
if(digits==null || digits.length()==0) {
return new ArrayList<>();
}
iterStr(digits, new StringBuilder(), 0);
return res;
}
//最终输出结果的list
List<String> res = new ArrayList<>();
//递归函数
void iterStr(String str, StringBuilder letter, int index) {
//递归的终止条件,注意这里的终止条件看上去跟动态演示图有些不同,主要是做了点优化
//动态图中是每次截取字符串的一部分,"234",变成"23",再变成"3",最后变成"",这样性能不佳
//而用index记录每次遍历到字符串的位置,这样性能更好
if(index == str.length()) {
res.add(letter.toString());
return;
}
//获取index位置的字符,假设输入的字符是"234"
//第一次递归时index为0所以c=2,第二次index为1所以c=3,第三次c=4
//subString每次都会生成新的字符串,而index则是取当前的一个字符,所以效率更高一点
char c = str.charAt(index);
//map_string的下表是从0开始一直到9, c-'0'就可以取到相对的数组下标位置
//比如c=2时候,2-'0',获取下标为2,letter_map[2]就是"abc"
int pos = c - '0';
String map_string = letter_map[pos];
//遍历字符串,比如第一次得到的是2,页就是遍历"abc"
for(int i=0;i<map_string.length();i++) {
//调用下一层递归,用文字很难描述,请配合动态图理解
letter.append(map_string.charAt(i));
//如果是String类型做拼接效率会比较低
//iterStr(str, letter+map_string.charAt(i), index+1);
iterStr(str, letter, index+1);
letter.deleteCharAt(letter.length()-1);
}
}
}