参考：Verilog学习笔记——有符号数的乘法和加法

一、无符号数、有符号数

将输入输出全部定义为有符号数

（1）无符号数的读取按照原码进行，有符号数的读取应该按照补码读取，计算规则为去掉符号位后取反、加1在计算数值。

（2）直接赋值十进制数据，乘数在以无符号数读取时时按照原码读取，127就对应 8 位二进制数 8’b0111_1111，十进制 128 就对应 8 位二进制 8’b1000_0000；而以有符号数读取的时候是会直接转换为补码形式，如 -127，先去掉符号位是 127，对应 7 位二进制数 7’b111_1111，取反为 7’b000_0000，加 1 为 7’b000_0001，将符号位补回到最高位为 8’b1000_0001；对于 -128 的表示比较特殊，8-bit的二进制数最高位是符号位，表示正负，剩下的 7-bit 能够表示的数的范围是 0 ~ 127，前面加上 ± 就能表示 -127 ~ 127，其中有 2 个数很特殊就是 8’b0000_0000 和 8’b1000_0000，按照上面会出现 +0 和 -0，为了区分出这两个数，前人定义 8’b0000_0000 表示 0，而 8’b1000_0000 表示 -128，这样不仅能区分开两个数，还多表示了一个数 -128（整个计算机体系通用，其他位数时类似表示一个负数）

（3）计算准则：

                 无符号 * 无符号 = 无符号；

                 有符号 * 有符号 = 有符号；

                 如果表达式中有一个无符号数，则所有的操作数都会被强行转换为无符号数；

当后面设计输入输出时，如果是有符号，那么将相关计算的输入/输出和中间量都显式的用 signed 定义。（如果是有符号数的计算，那么所有的输入、输出、中间量的计算都应该设置为有符号数）

符号扩展计算方法：

计算准则：

对于乘法，在运算的时候将符号位扩展到和积的位数相等。一般使用位拼接符{}进行计算。

对有符号数的加法，同样的，要么相关的运算全部定义成有符号数，要么进行符号位的扩展，对于加法操作，只需要每个被加数扩展 1 位符号位即可；

---

参考：Verilog学习笔记——有符号数的乘法和加法

案例：

下面的输入和输出都没有指定成 signed 有符号数，计算时默认是按照无符号数计算（是把读取到的 8 位二进制数当做原码去算），此时若外部传入的数据实际上是有符号数（比如 FIR 滤波器传入了正负均有的待滤波信号），那么需要对符号位进行扩展来计算乘法和加法；

module signed_test_2(
    input   [7:0]   data_in_1,
    input   [7:0]   data_in_2,
    output  [15:0]  data_out_1,
    output  [15:0]  data_out_2
);

对于乘法，需要扩展符号位 到 和积的位数相等，比如乘数a为 N-bit，乘数 b 为M-bit，两个相乘得到 N+M 位数据，此时需要对 a 扩展 M-bit 到 N+M 位，对 b 扩展 N-bit 到 N+M 位；

下面，使用 位拼接符 { } 来做演示，位拼接符可以按照二进制的位来进行高低位的拼接，假设 data_in_1= 8’b1000_0011，对于 {{8{data_in_1[7]}},data_in_1} 可以这样理解：

（1） 先看 8{data_in_1[7]}，表示取出 8-bit 数据 data_in_1 的最高位 data_in_1[7]，重复 8 次，相当于 { data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7] }，即高位扩展 8-bit 的 1

（2） {{8{data_in_1[7]}},data_in_1} 相当于在 data_in_1 的前面补上 8 个 data_in_1[7]，即 结果为 16-bit 的 16’b1111_1111_1000_0011；

//不做符号位扩展，直接相乘
assign data_out_1 = data_in_1 * data_in_2;
//做符号位扩展，再相乘
assign data_out_2 = {{8{data_in_1[7]}},data_in_1} * {{8{data_in_2[7]}},data_in_2};

仿真测试数据如下，1 处用十六进制给出数据，2 处用有符号的十进制赋值，3 处是为了和 2 处对比，看最后赋值是否一样；

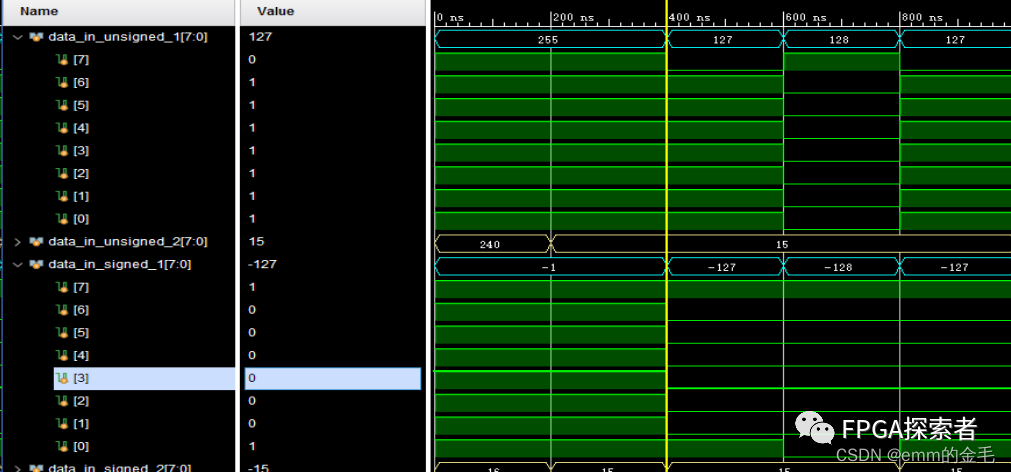
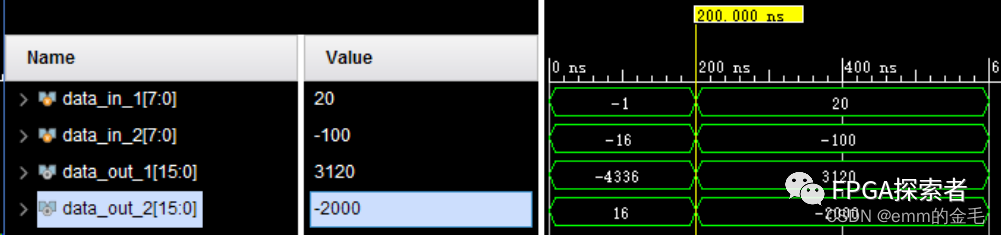
仿真结果如下，可以看到上图 2 处和 3 处的赋值在仿真时是同样的数据，把所有数据都用有符号的十进制数显示（右键数据 Radix -> Signed Decimal）

 （可以看到对于负数数据的读入是将其补码读入）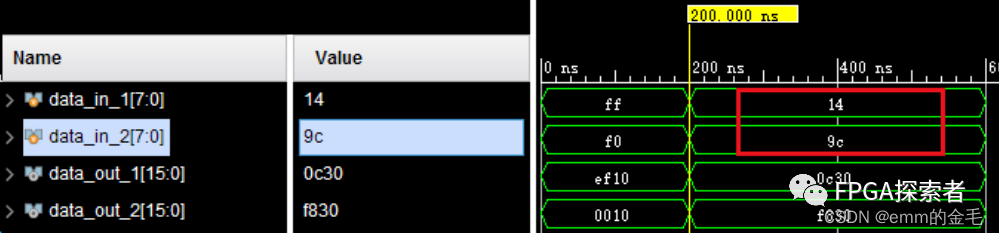

可以看到，data_out_1的结果是错的（没有补符号位），data_out_2的结果是对的（补符号位）；

利用IP进行计算

除此之外，还可以调用乘法器的 IP 来代替 乘法符号 *，或者加法器的 IP 来代替 加法符号 +，在 IP 核中配置输入输出为有符号数即可

二、有符号位的位宽匹配问题

参考：verilog有符号数的位宽转换_verilog 有符号数位宽大到位宽小-CSDN博客

当有符号低位宽向高位宽匹配时，高位需要补充符号位。

reg [3:0]	original;								//定义4位有符号数寄存器变量
reg [7:0]	later;									//定义8位有符号数寄存器变量
assign later = {{4{original[3]}}},original};		//高4位补original的符号位

当有符号高位宽向低位宽匹配时，直接对于低位进行截取，当然在这个过程中可能会将符号位截掉。

对于短位宽赋值给长位宽的情况，需要对高位进行位扩展，具体是扩展1还是扩展0，记住：完全依据右操作数!，具体如下：
1）右操作数是无符号数，则无论左操作数是什么类型，高位都扩展成0；
2）右操作数是有符号数，则要看右操作数的符号位，按照右操作数的符号位扩展，符号位是1就扩展1，是0就扩展0；
3）位扩展后的左操作按照是无符号数还是有符号数解释成对应的十进制数值，如果是无符号数，则直接转换成十进制数值，如果是有符号数，则看成2的补码解释成十进制数；
4）从上面4种情况看出，有符号数赋值成无符号数会出现数据错误的情况，因此要避免这种赋值，而其他情况都是可以保证数据正确的。

                   
引自：https://blog.csdn.net/qq_31006535/article/details/106216391

三、例子 

1. 题目

根据指示信号select的不同，对输入信号a,b实现不同的运算。输入信号a、b为8bit有符号数，

当select[1:0] = 0，输出a；

当select[1:0] = 1，输出b；

当select[1:0] = 2，输出a+b；

当select[1:0] = 3，输出a-b。

 思路：有符号数的加减法有两种方式

（1）将有符号数输入、输出、中间变量全部定义为有符号数

注意：如果在运算工程中出现无符号数，那么在运算的过程中都会将有符号数（补码形式）视为无符号数参与计算

（2）采用符号位扩展的方式进行运算

`timescale 1ns/1ns
module data_select(
  input clk,
  input rst_n,
  input signed[7:0]a,
  input signed[7:0]b,
  input [1:0]select,
  output reg signed [8:0]c
);

always@(posedge clk,negedge rst_n)begin
    if(~rst_n)begin
        c <= 9'b0;
    end
    else begin
        case(select)
            2'b00: c<= {a[7],a};
            2'b01: c<= {b[7],a};
            2'b10: c<= {a[7],a} + {b[7],a};
            2'b11: c<= {a[7],a} - {b[7],a};
        endcase
    end
end
endmodule