Python的核心语言元素: (变量、类型、运算符、表达式、分支结构、循环结构)
之后,必须做的一件事情就是尝试用所学知识去解决现实中的问题,换句话说就是锻炼自己把用人类自然语言描述的算法(解决问题的方法和步骤)翻译成Python代码的能力,而这件事情必须通过大量的练习才能达成。
经典实例:
1.寻找水仙花数。
说明:水仙花数也被称为超完全数字不变数、自恋数、自幂数、阿姆斯特朗数,它是一个3位数,该数字每个位上数字的立方之和正好等于它本身,例如:$1^3 + 5^3+ 3^3=153$。
"""
找出所有水仙花数
Version: 0.1
Author: Maxwell
"""
for num in range(100, 1000):
low = num % 10
mid = num // 10 % 10
high = num // 100
if num == low ** 3 + mid ** 3 + high ** 3:
print(num) 
我们通过整除和求模运算分别找出了一个三位数的个位、十位和百位,这种小技巧在实际开发中还是常用的。用类似的方法,我们还可以实现将一个正整数反转,例如:将12345变成54321,代码如下所示。
"""
正整数的反转
Version: 0.1
Author: Maxwell
"""
num = int(input('num = '))
reversed_num = 0
while num > 0:
reversed_num = reversed_num * 10 + num % 10
num //= 10
print(reversed_num)2.百钱百鸡问题。
说明:百钱百鸡是我国古代数学家张丘建在《算经》一书中提出的数学问题:鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?翻译成现代文是:公鸡5元一只,母鸡3元一只,小鸡1元三只,用100块钱买一百只鸡,问公鸡、母鸡、小鸡各有多少只?
"""
《百钱百鸡》问题
Version: 0.1
Author: Maxwell
"""
for x in range(0, 20):
for y in range(0, 33):
z = 100 - x - y
if 5 * x + 3 * y + z / 3 == 100:
print('公鸡: %d只, 母鸡: %d只, 小鸡: %d只' % (x, y, z))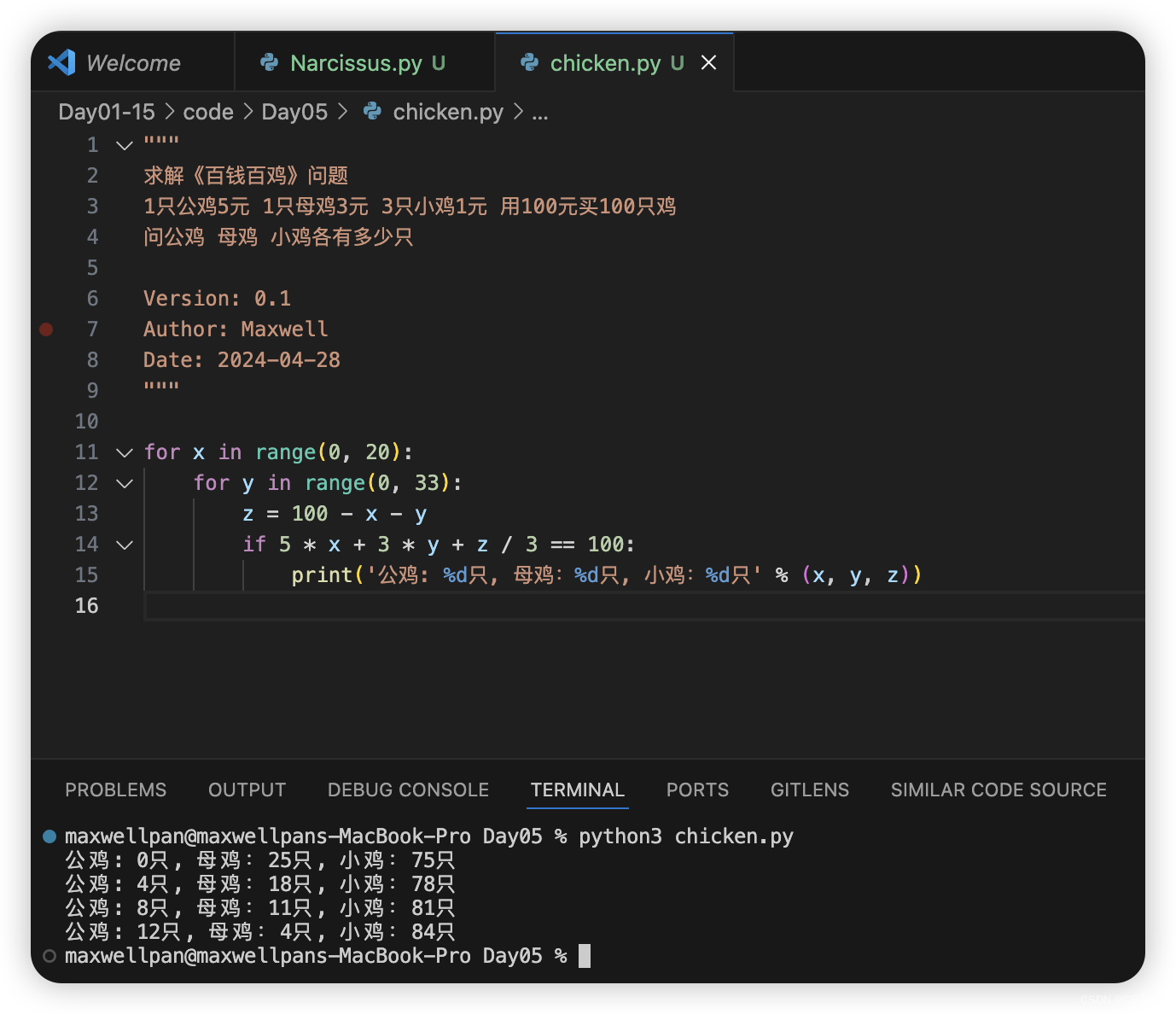
上面使用的方法叫做穷举法,也称为暴力搜索法,这种方法通过一项一项的列举备选解决方案中所有可能的候选项并检查每个候选项是否符合问题的描述,最终得到问题的解。这种方法看起来比较笨拙,但对于运算能力非常强大的计算机来说,通常都是一个可行的甚至是不错的选择,而且问题的解如果存在,这种方法一定能够找到它。
3.CRAPS赌博游戏。
说明:CRAPS又称花旗骰,是美国拉斯维加斯非常受欢迎的一种的桌上赌博游戏。该游戏使用两粒骰子,玩家通过摇两粒骰子获得点数进行游戏。简单的规则是:玩家第一次摇骰子如果摇出了7点或11点,玩家胜;玩家第一次如果摇出2点、3点或12点,庄家胜;其他点数玩家继续摇骰子,如果玩家摇出了7点,庄家胜;如果玩家摇出了第一次摇的点数,玩家胜;其他点数,玩家继续要骰子,直到分出胜负。
"""
Craps赌博游戏
我们设定玩家开始游戏时有1000元的赌注
游戏结束的条件是玩家输光所有的赌注
Version: 0.1
Author: Maxwell
"""
from random import randint
money = 1000
while money > 0:
print('你的总资产为:', money)
needs_go_on = False
while True:
debt = int(input('请下注: '))
if 0 < debt <= money:
break
first = randint(1, 6) + randint(1, 6)
print('玩家摇出了%d点' % first)
if first == 7 or first == 11:
print('玩家胜!')
money += debt
elif first == 2 or first == 3 or first == 12:
print('庄家胜!')
money -= debt
else:
needs_go_on = True
while needs_go_on:
needs_go_on = False
current = randint(1, 6) + randint(1, 6)
print('玩家摇出了%d点' % current)
if current == 7:
print('庄家胜')
money -= debt
elif current == first:
print('玩家胜')
money += debt
else:
needs_go_on = True
print('你破产了, 游戏结束!')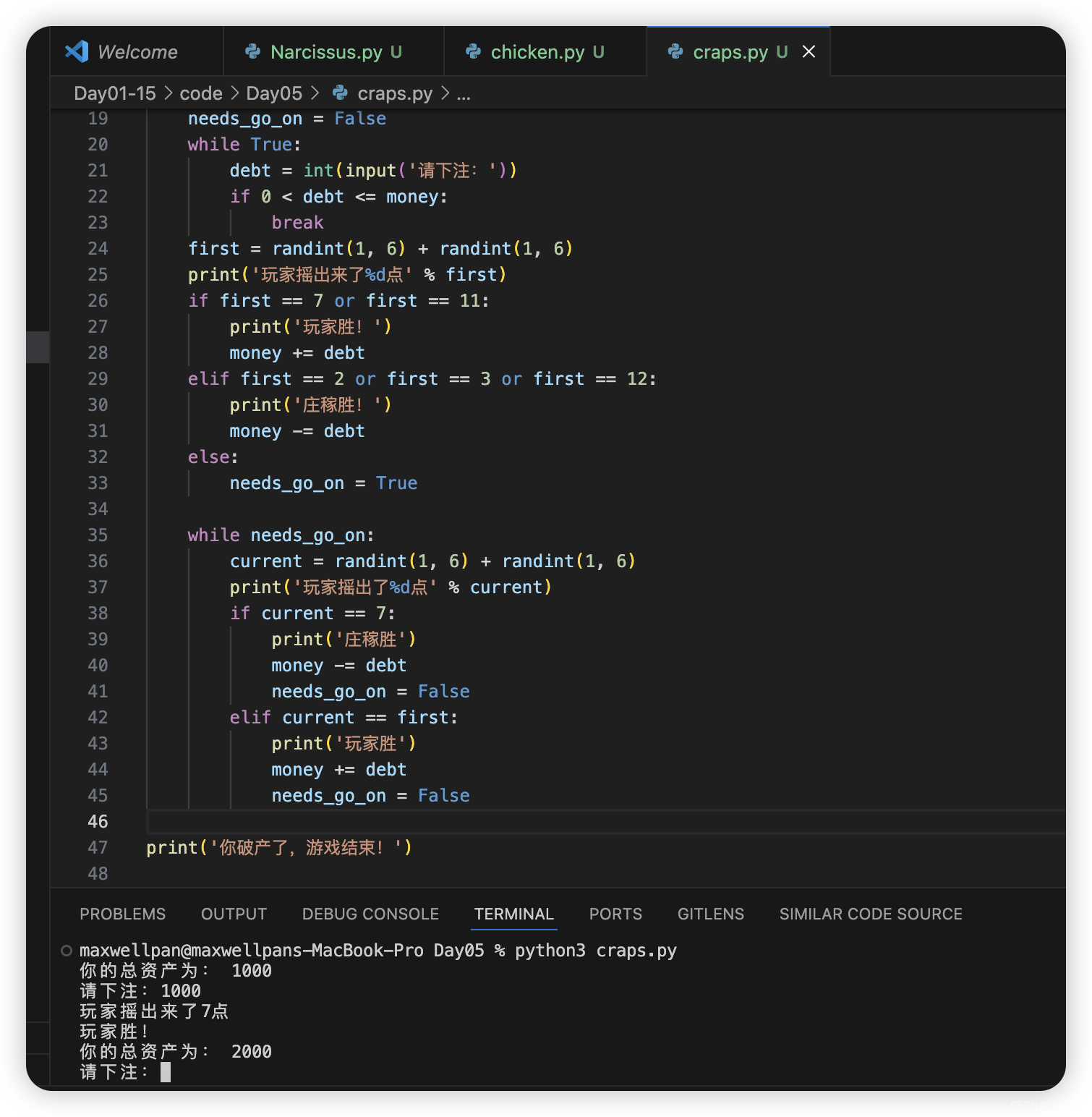
4.生成斐波那契数列的前20个数。
说明:斐波那契数列(Fibonacci sequence),又称黄金分割数列,是意大利数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)在《计算之书》中提出一个在理想假设条件下兔子成长率的问题而引入的数列,所以这个数列也被戏称为"兔子数列"。斐波那契数列的特点是数列的前两个数都是1,从第三个数开始,每个数都是它前面两个数的和,形如:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...。斐波那契数列在现代物理、准晶体结构、化学等领域都有直接的应用。
"""
输出斐波那契数列的前20个数
1 1 2 3 5 8 13 21 ...
Version: 0.1
Author: Maxwell
Date: 2024-04-28
"""
a = 0
b = 1
for _ in range(20):
a, b = b, a + b
print(a, end=' ')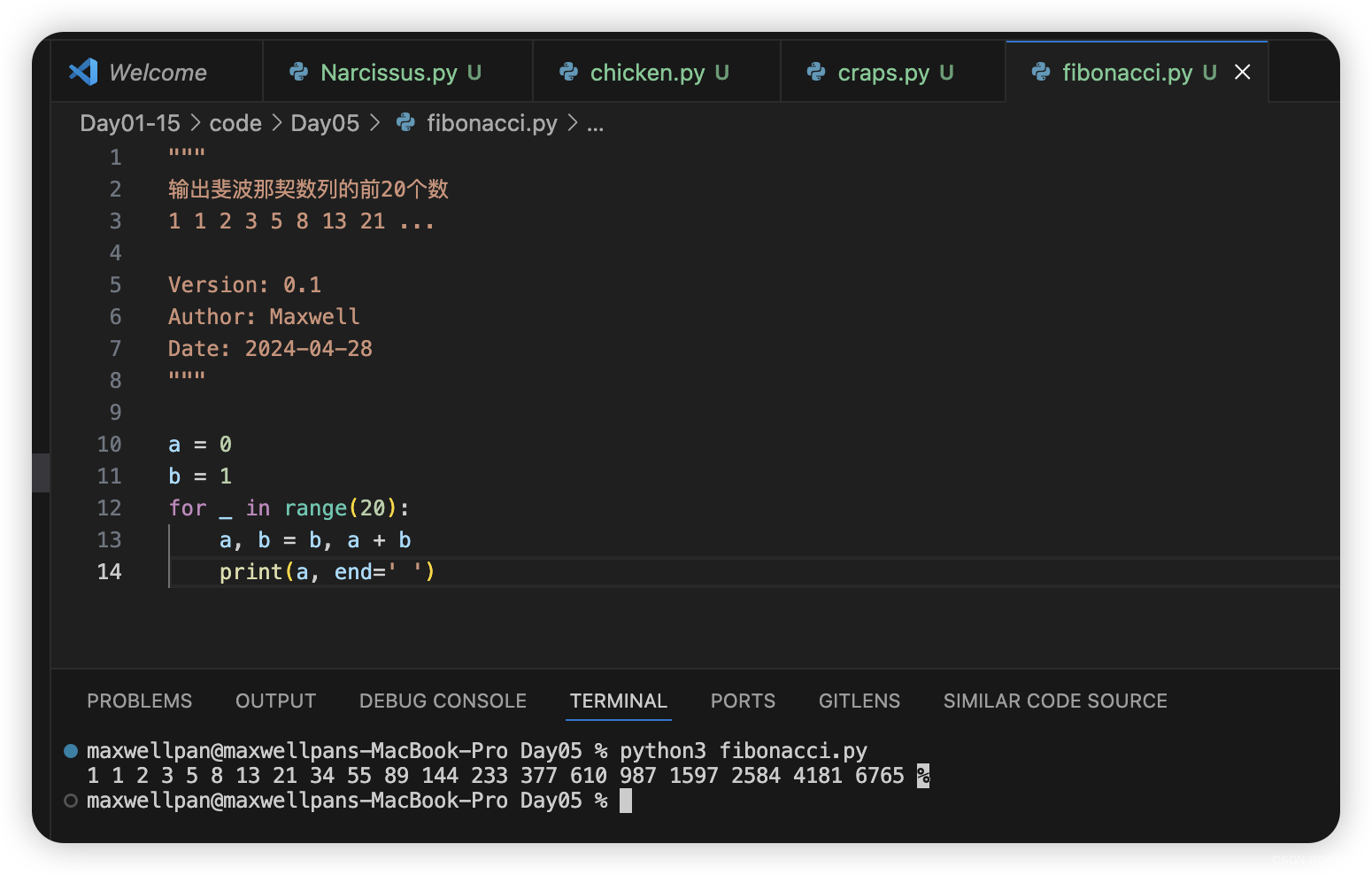
5.找出10000以内的完美数。
说明:完美数又称为完全数或完备数,它的所有的真因子(即除了自身以外的因子)的和(即因子函数)恰好等于它本身。例如:6($6=1+2+3$)和28($28=1+2+4+7+14$)就是完美数。完美数有很多神奇的特性,有兴趣的可以自行了解。
"""
找出1~9999之间的所有完美数
完美数是除自身外其他所有因子的和正好等于这个数本身的数
例如: 6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14
Version: 0.1
Author: Maxwell
Date: 2024-04-28
"""
import math
for num in range(2, 10000):
result = 0
for factor in range(1, int(math.sqrt(num)) + 1):
if num % factor == 0:
result += factor
if factor > 1 and num // factor != factor:
result += num // factor
if result == num:
print(num)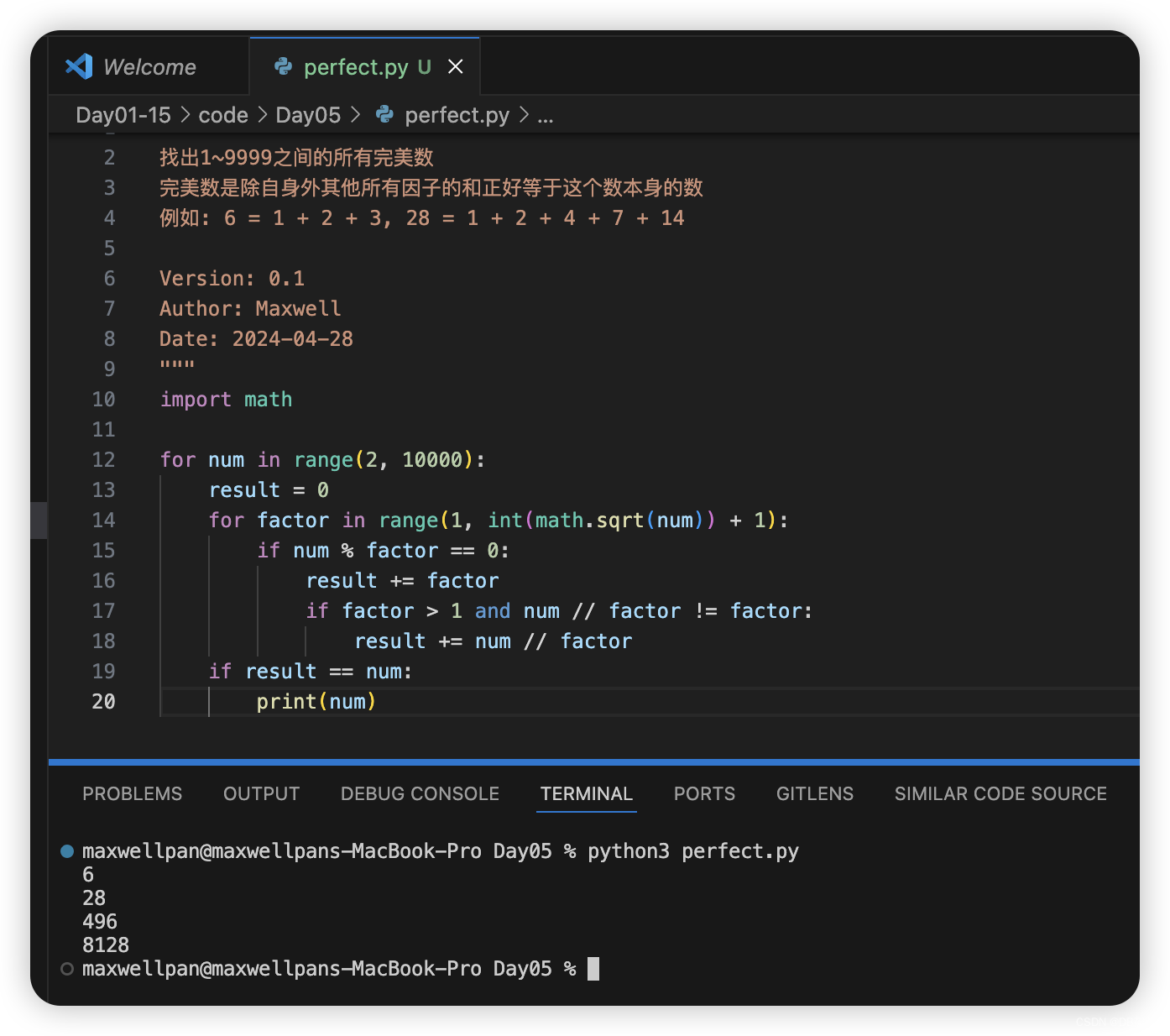
6.输出100以内所有的素数。
说明:素数指的是只能被1和自身整除的正整数(不包括1)。

"""
输出2~99之间的素数
Version: 0.1
Author: Maxwell
Date: 2024-04-28
"""
import math
for num in range(2, 100):
is_prime = True
for factor in range(2, int(math.sqrt(num)) + 1):
if num % factor == 0:
is_prime = False
break
if is_prime:
print(num, end=' ')倘若您觉得我写的好,那么请您动动你的小手粉一下我,你的小小鼓励会带来更大的动力。Thanks.