本文是观看以下视频的笔记：
https://www.bilibili.com/video/BV1CU4y1i7jn/?p=4&spm_id_from=pageDriver

其他参考
https://zhuanlan.zhihu.com/p/614147698
https://zhuanlan.zhihu.com/p/563661713

这个写的非常详细：
https://www.zhihu.com/question/574586781/answer/3001481574

符号定义

• xT: 符合高斯分布的噪声
• x0: 一个符合GT的图像，无噪声的，clean image
• T: 时间步
• xt: 第t步的图像，要从他推出t-1的图像。（一直推下去的话可以推出x0）
• ${\beta }_t$：noise rate，关于t的固定序列，含义是每一步t要加的噪声的比例。
• ${\alpha }_t$：signal rate，关于t的固定序列，${\alpha }_t$= 1-${\beta }_t$，含义是每一步t保留的上一步图像比例。通常会被设置为${\lim }_{t\to T}{\alpha }_t=0$。具体定义是：${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{\mathbf{ϵ}}_t$
• q：正向扩散：加噪声
• p：逆向扩散：去噪声
• ${\mathbf{ϵ}}_t$ 或${\mathbf{z}}_t$: xt相比xt-1加的噪声，服从标准正态分布。本文中z和epsilon混用
• $\mathbf{ϵ}$：不是t这一步的噪声，而是前面的噪声叠加后的结果，还是以服从标准正态分布
• z波浪：网络预测的噪声，希望他尽可能接近真实的z

概述

https://www.bilibili.com/video/BV16N4y177Wk/?spm_id_from=333.788&

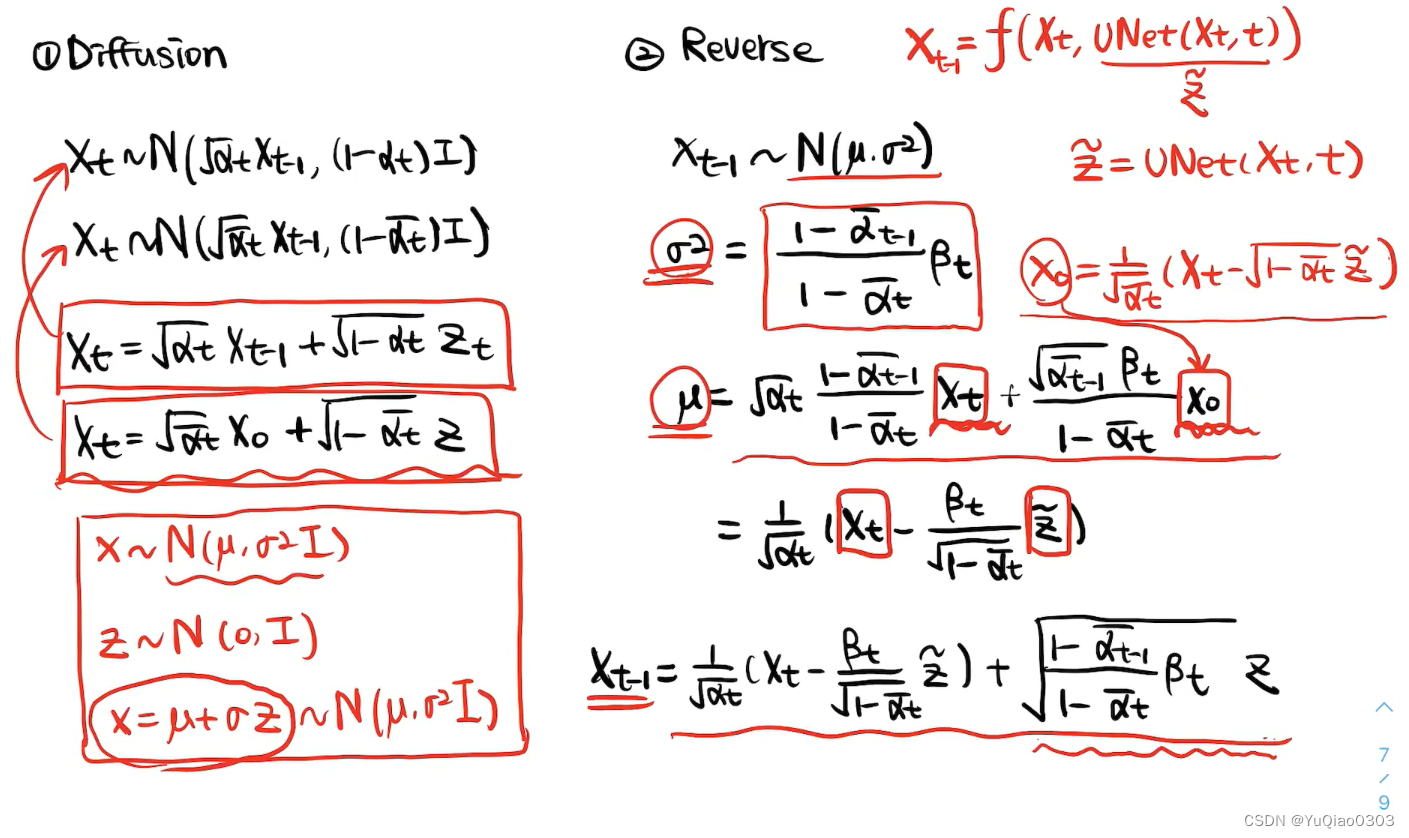
加噪（Forward，training）

初始定义：$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)$

(“:=” 是定义为的意思)

• $q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right):=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1},(1-{\alpha }_t\right)\mathbf{I})$ 或$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)\sim \mathcal{N}\left(\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1},(1-{\alpha }_t\right)\mathbf{I})$, 也即
• ${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{\mathbf{ϵ}}_t$， 其中 ${\mathbf{ϵ}}_{t-1}\sim \mathcal{N}(0,1)$

使用重参数技巧一步步展开可得：$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)$

• $q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,\left(1-{\bar{\alpha }}_t\right)\mathbf{I}\right)$ 或$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)\sim \mathcal{N}\left(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,(1-{\bar{\alpha }}_t\right)\mathbf{I})$也即

• ${\mathbf{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ}$， 其中${\bar{\alpha }}_t={\prod }_{i=1}^t{\alpha }_i$, $\mathbf{ϵ}\sim \mathcal{N}(0,1)$。

• 注意区分“每一步t的噪声 ${\mathbf{ϵ}}_t$”和“他们叠加后的噪声$\mathbf{ϵ}$ ”，

  • 叠加公式是$\mathrm{a}{\mathrm{X}}_1+\mathrm{b}{\mathrm{X}}_2\sim N\left(\mathrm{a}{\mu }_1+b{\mu }_2,{\mathrm{a}}^2{\sigma }_1^2+b^2{\sigma }_2^2\right)$）

• 具体推导过程如下：

• $$\begin{array}{rl}{\mathbf{x}}_t& =\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\\ & =\sqrt{{\alpha }_t}(\sqrt{{\alpha }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{ϵ}_{t-1})+\sqrt{1-{\alpha }_t}{ϵ}_t\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{{\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}}^2+{\sqrt{1-{\alpha }_t}}^2}{\overline{ϵ}}_{t-1};两个相互独立的正态分布的叠加仍是正态分布\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\overline{ϵ}}_{t-1}\\ & =\dots \\ & =\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}ϵ\end{array}$$

或者看下图：

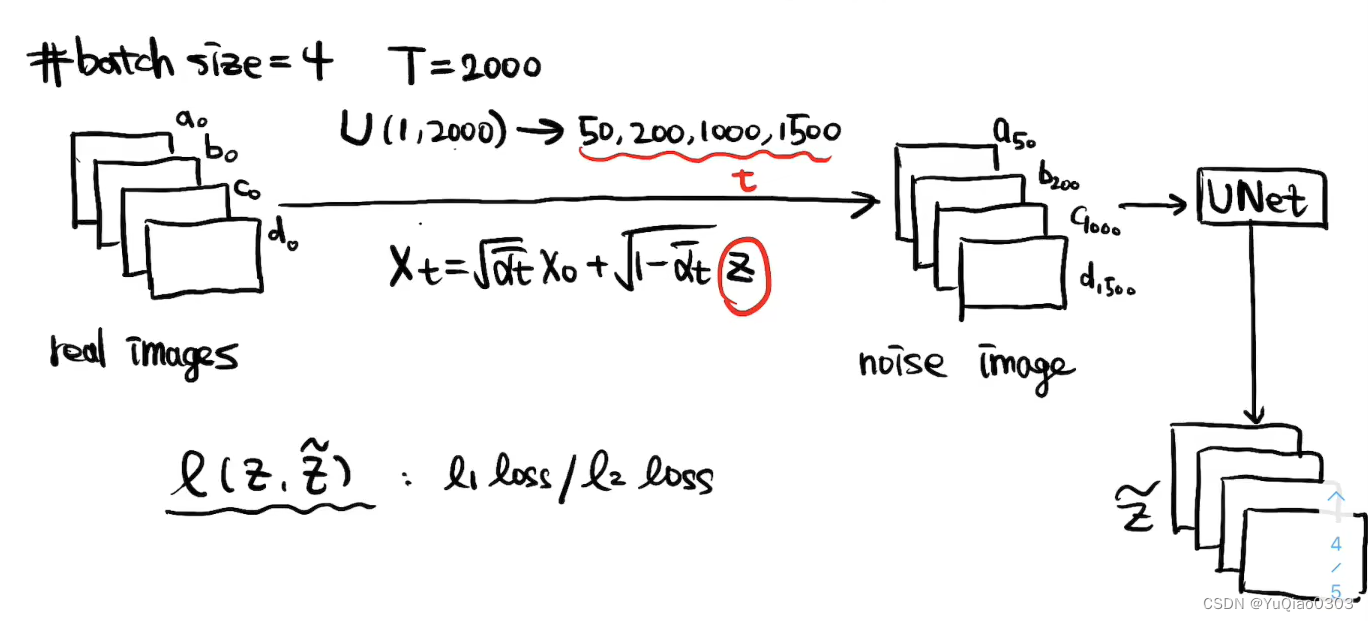
training

• 每一个不同的t，对应的噪声都是不同的（重新随机采的）！
• 网络预测不是某一步相比上一步增加的噪声${\mathbf{ϵ}}_t$，而是${\mathbf{ϵ}}_t$,${\mathbf{ϵ}}_{t-1}$…最后叠加得到的$\mathbf{ϵ}$
  
  

去噪（Reverse, inference, sampling）

目标是$p({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)$

现在我们有: $q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})$ ，$q({\mathbf{x}}_t\mid {\mathbf{x}}_0)$ ，$p({\mathbf{x}}_T)=\mathcal{N}({\mathbf{x}}_T;0,\mathbf{I})$
要求的是: $p({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$ 。
这个东西不好弄，我们改为求$p({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)$

开始，
$$\begin{array}{rl}& p({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\\ & =p({\mathbf{x}}_t|{\mathbf{x}}_{t-1},{\mathbf{x}}_0)\frac{p({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}{p({\mathbf{x}}_t|{\mathbf{x}}_0)}(贝叶斯公式)\\ & =p({\mathbf{x}}_t|{\mathbf{x}}_{t-1})\frac{p({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}{p({\mathbf{x}}_t|{\mathbf{x}}_0)}（马尔科夫假设）\end{array}$$

第一个等号：贝叶斯公式（将右边分母挪到左边后，两边就都是x0条件下xt-1和xt同时发生的概率）
第二个等号：由于从t-1到t这个加噪的过程是马尔科夫过程，即xt只与xt-1有关，而与更小的时间步无关，所以$p({\mathbf{x}}_t|{\mathbf{x}}_{t-1},{\mathbf{x}}_0)=p({\mathbf{x}}_t|{\mathbf{x}}_{t-1},{\mathbf{x}}_0)$

最后的这三项都是已知的：
$$\begin{gathered} p\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right):=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1},(1-{\alpha }_t\right)\mathbf{I}) \\ q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,\left(1-{\bar{\alpha }}_t\right)\mathbf{I}\right) \\ q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0\right)=\mathcal{N}\left({\mathbf{x}}_{t-1};\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0,\left(1-{\bar{\alpha }}_{t-1}\right)\mathbf{I}\right) \end{gathered}$$

考虑到：
$$\begin{gathered} 正态分布f(x)=\frac{1}{\sigma \sqrt{2\pi }}e-\frac{(x-\mu )2}{2{\sigma }^2} \\ f(x)\propto e-\frac{(x-\mu )2}{2{\sigma }^2} \end{gathered}$$
把所有的正态分布换成这个正比于的表达方式，我们凑一下 $p({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)$ 也写成这个形式：

下方的推导有以下注意点：

• exp指数部分的常数如果拿到exp外面， 不影响“正比于”这件事，因此我们都忽略掉；
• 注意，由于目标是$p({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$，我们最后的结果中只保留xt这个变量，用xt和预测的z波浪来表达x0

重参数技巧：写成一个新的正态分布，并表示出其均值和方差

$$\begin{array}{rl}& p({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\\ & =p({\mathbf{x}}_t|{\mathbf{x}}_{t-1})\frac{p({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}{p({\mathbf{x}}_t|{\mathbf{x}}_0)}\\ & \propto \exp \left\{-\frac{1}{2}\left(\frac{{\left(x_t-\sqrt{{\alpha }_t}{x}_{t-1}\right)}^2}{1-{\alpha }_t}+\frac{{\left(x_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{x}_0\right)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{{\left(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0\right)}^2}{1-{\bar{\alpha }}_t}\right)\right\}\end{array}$$

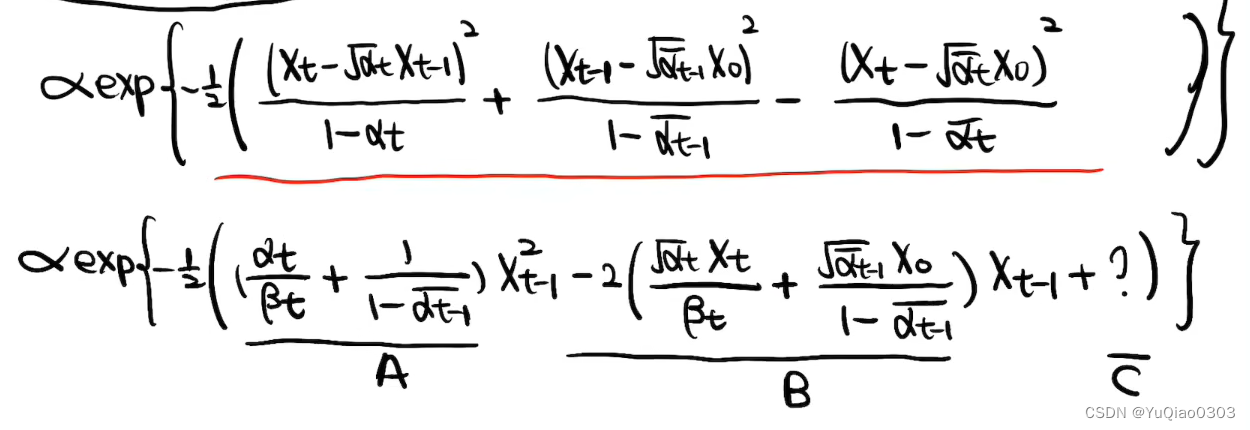
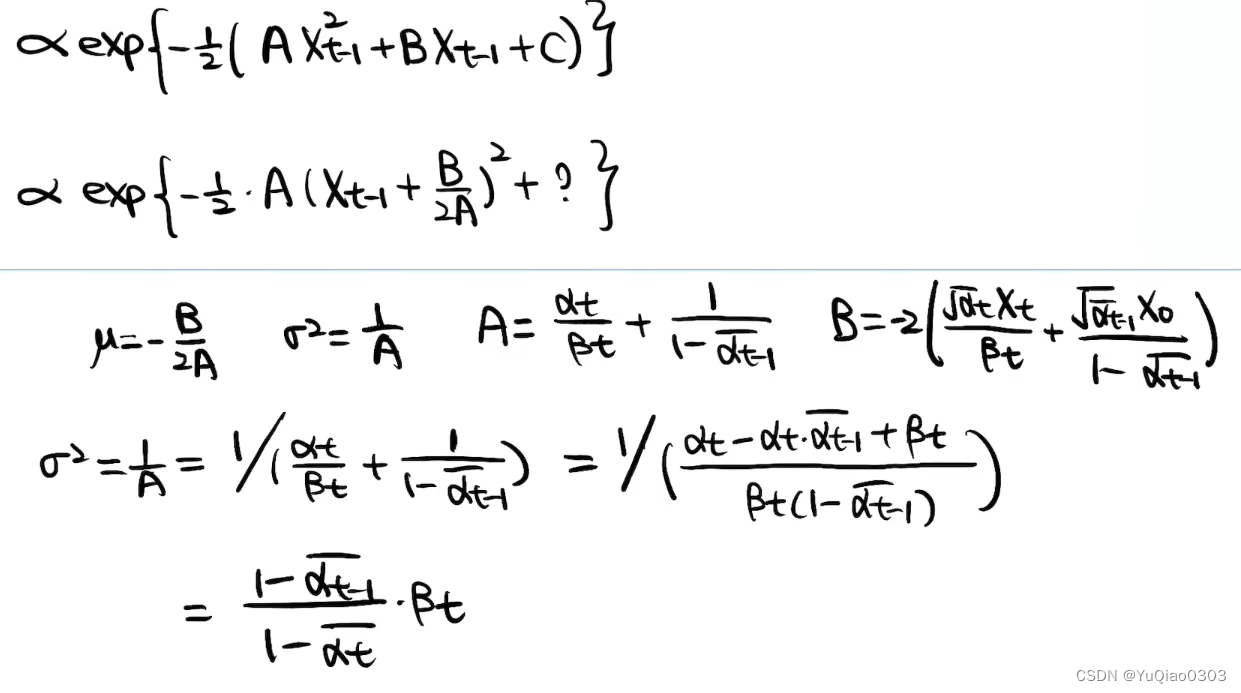
至此得到了方差，发现是固定的常数。下面继续求均值μ。
注意

• 我们在这里把x0 用xt和网络预测的噪声z波浪来表示，从而消掉x0并引入z波浪
• 下面没有等号的两行是单独的，要带进μ的等式的内容
  

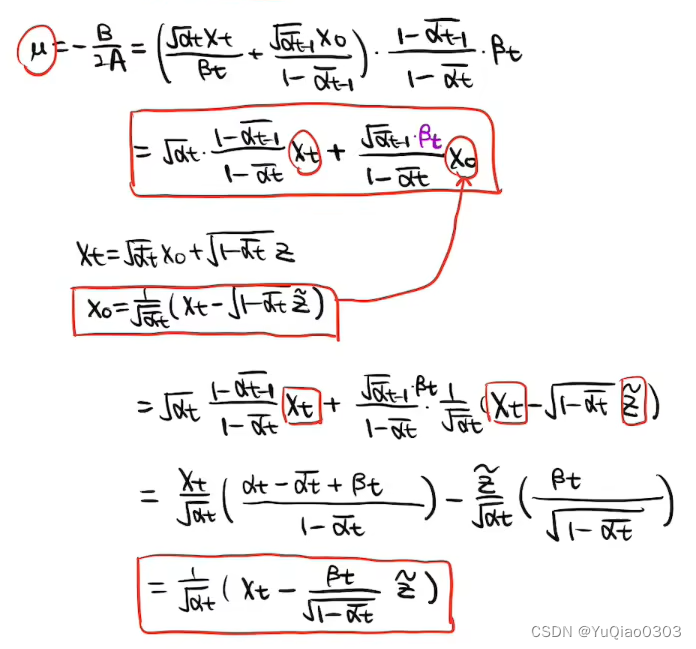
去噪总结

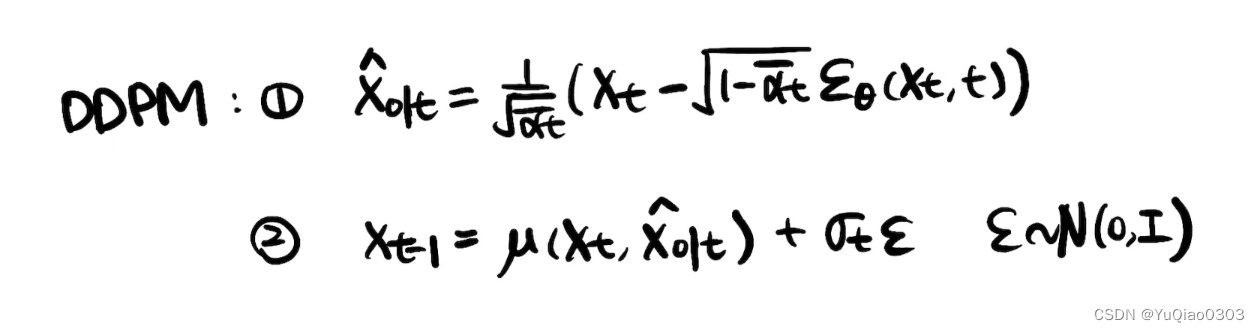
至此，我们求出了
$$\begin{gathered} p({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\propto \mathcal{N}(\mu ,{\sigma }^2)，其中 \\ {\sigma }^2=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t, \\ \mu =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{\mathbf{x}}_0 \\ =\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-\overline{{\alpha }_t}}}\hat{z}) \end{gathered}$$

也就是说，如果已知x0和xt,那么xt-1满足一个标准正态分布，其方差是常数，均值与网络预测的z波浪有关
因此，根据正态分布的重参数化技巧，
$$\begin{array}{rl}& p({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\\ & =\mu +\sigma \mathbf{z}\\ & =\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-\overline{{\alpha }_t}}}\hat{z})+\sqrt{\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t}\mathbf{z}\end{array}$$
其中z属于标准正态分布。

那么，为什么这里最后的z要用一个噪声采样而不直接设为0呢？如果全0的话，其实概率很低，符合正态分布的概率更高一些。

Sampling

上面那个式子直接就可以写成这样了，问题仅在于，我们省略的常数去哪 里了。不知道，可能刚好算出来还是没了吧。

• 这个sigma t不一定要等于刚才求的那个标准差，比它小也行。
• 注意，最后一步不再加噪声了