文章目录
- 前言
- 一、梯度替代
- 二、网络结构
- 三、MNIST分类
- 1、单步模式
- 2、多步模式
- 总结
前言
在SpikingJelly使用梯度替代训练SNN,构建单层全连接SNN实现MNIST分类任务。
一、梯度替代
1、梯度替代:
阶跃函数不可微,无法进行反向传播
g ( x ) = { 1 , x ≥ 0 0 , x < 0 g(x) = \left\{\begin{matrix} 1,&\quad x\ge 0\\ 0,&\quad x<0\\ \end{matrix}\right. g(x)={1,0,x≥0x<0 , ,\quad\quad\quad , g ′ ( x ) = { + ∞ , x = 0 0 , x ≠ 0 g^{\prime}(x) = \left\{\begin{matrix} +∞&,\quad x= 0\\ 0&,\quad x\neq0\\ \end{matrix}\right. g′(x)={+∞0,x=0,x=0
前向传播使用阶跃函数,反向传播使用替代函数
2、梯度替代函数:
来源:spikingjelly.activation_based.surrogate package
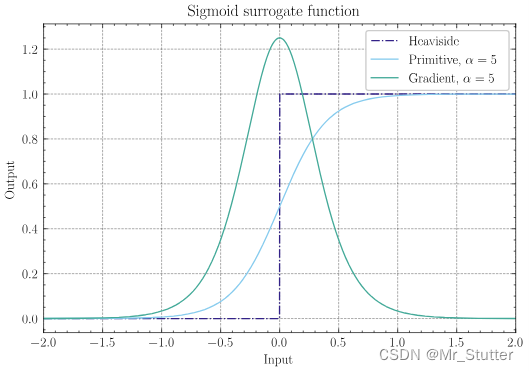
①Sigmoid:surrogate.Sigmoid(alpha=4.0, spiking=True)
g ( x ) = s i g m o i d ( α x ) = 1 1 + e − α x g(x) = sigmoid(\alpha x)=\frac{1}{1+e^{-\alpha x}} g(x)=sigmoid(αx)=1+e−αx1
g ′ ( x ) = α ∗ s i g m o i d ( α x ) ∗ ( 1 − s i g m o i d ( α x ) ) g^{\prime}(x) = \alpha*sigmoid(\alpha x)*(1-sigmoid(\alpha x)) g′(x)=α∗sigmoid(αx)∗(1−sigmoid(αx))
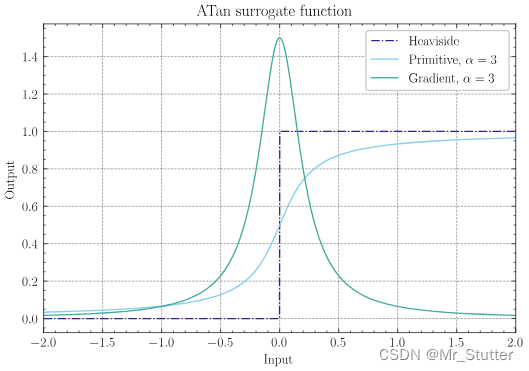
②ATan:surrogate.ATan(alpha=2.0, spiking=True)
g ( x ) = 1 π a r c t a n ( π 2 α x ) + 1 2 g(x) = \frac{1}{\pi}arctan(\frac{\pi}{2}\alpha x)+\frac{1}{2} g(x)=π1arctan(2παx)+21
g ′ ( x ) = α 2 ( 1 + ( π 2 α x ) 2 ) g^{\prime}(x) = \frac{\alpha}{2(1+(\frac{\pi}{2}\alpha x)^2)} g′(x)=2(1+(2παx)2)α
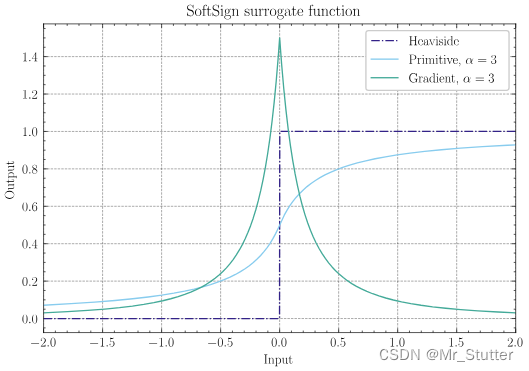
③SoftSign:surrogate.SoftSign(alpha=2.0, spiking=True)
g ( x ) = 1 2 ( α x 1 + ∣ α x ∣ + 1 ) g(x) = \frac{1}{2}(\frac{\alpha x}{1+|\alpha x|}+1) g(x)=21(1+∣αx∣αx+1)
g ′ ( x ) = α 2 ( 1 + ∣ α x ∣ 2 ) g^{\prime}(x) = \frac{\alpha}{2(1+|\alpha x|^2)} g′(x)=2(1+∣αx∣2)α
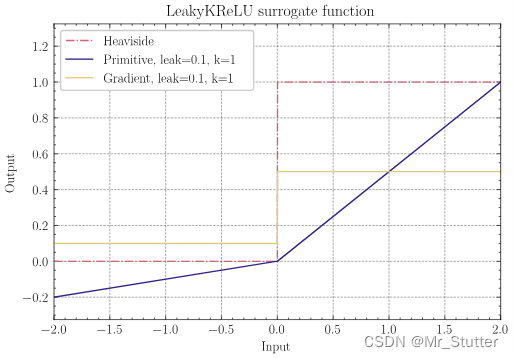
④LeakyKReLU:surrogate.LeakyKReLU(spiking=True, leak: float=0.0, k: float=1.0)
g ( x ) = { k ∗ x , x ≥ 0 l e a k ∗ x , x < 0 g(x) = \left\{\begin{matrix} k*x,&\quad x\ge 0\\ leak*x,&\quad x<0\\ \end{matrix}\right. g(x)={k∗x,leak∗x,x≥0x<0 , ,\quad\quad\quad , g ′ ( x ) = { k , x ≥ 0 l e a k , x < 0 g^{\prime}(x) = \left\{\begin{matrix} k&,\quad x\ge 0\\ leak&,\quad x<0\\ \end{matrix}\right. g′(x)={kleak,x≥0,x<0
二、网络结构
使用神经元层替代激活函数
1、ANN
nn.Sequential(
nn.Flatten(),
nn.Linear(28 * 28, 10, bias=False),
nn.Softmax()
)
2、SNN
nn.Sequential(
layer.Flatten(),
layer.Linear(28 * 28, 10, bias=False),
neuron.LIFNode(tau=tau, surrogate_function=surrogate.ATan())
)
三、MNIST分类
1、单步模式
(1)导入库
import time
import numpy as np
from matplotlib import pyplot as plt
import torch
from torch import nn, optim
from torch.utils.data import TensorDataset, DataLoader
from spikingjelly.activation_based import neuron, encoding,\
functional, surrogate, layer, monitor
from spikingjelly import visualizing
from load_mnist import load_mnist
(2)构建数据加载器
将numpy数据封装成DataLoader
使用Pytorch自带的数据集会更方便
def To_loader(x_train, y_train, x_test, y_test, batch_size):
# 转为张量
x_train = torch.from_numpy(x_train.astype(np.float32))
y_train = torch.from_numpy(y_train.astype(np.float32))
x_test = torch.from_numpy(x_test.astype(np.float32))
y_test = torch.from_numpy(y_test.astype(np.float32))
# 数据集封装
train_dataset = TensorDataset(x_train, y_train)
test_dataset = TensorDataset(x_test, y_test)
train_loader = DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=True)
return train_dataset, test_dataset, train_loader, test_loader
(3)构建SNN模型
将LIF神经元层当作激活函数使用
使用ATan作为梯度替代函数进行反向传播
class SNN(nn.Module):
def __init__(self):
super().__init__()
self.layer = nn.Sequential(
layer.Linear(784, 10, bias=False),
neuron.LIFNode(tau=2.0,
decay_input=True,
v_threshold=1.0,
v_reset=0.0,
surrogate_function=surrogate.ATan(),
step_mode='s',
store_v_seq=False)
)
def forward(self, x):
return self.layer(x)
(4)训练参数
使用泊松编码器对输入进行编码
取10000个样本进行训练
epoch_num = 10
batch_size = 256
T = 50
lr = 0.001
encoder = encoding.PoissonEncoder() # 泊松编码器
model = SNN() # 单层SNN
loss_function = nn.MSELoss() # 均方误差
optimizer = optim.Adam(model.parameters(), lr) # Adam优化器
x_train, y_train, x_test, y_test = \
load_mnist(normalize=True, flatten=False, one_hot_label=True)
train_dataset, test_dataset, train_loader, test_loader =\
To_loader(x_train[:10000], y_train[:10000], x_test, y_test, batch_size)
(5)迭代训练
①取一段时间的平均发放率作为输出
②损失函数采用交叉熵或均方差,使对应神经元fout→1,其他神经元fout→0
③每批训练后重置网络状态
④每轮训练后测试准确率
start_time = time.time()
loss_train_list = []
acc_train_list = []
acc_test_list = []
for epoch in range(epoch_num):
print('Epoch:%s'%(epoch+1))
# 模型训练
loss_train = 0
acc_train = 0
for x, y in train_loader:
f_out = torch.zeros((y.shape[0], 10)) # 输出频率
# 前向计算,逐步传播
for t in range(T):
encoded_x = encoder(x.reshape(-1, 784))
f_out += model(encoded_x)
f_out /= T
# 反向传播
loss = loss_function(f_out, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 计算损失值与准确率
loss_train += loss.item()
acc_train += (f_out.argmax(1) == y.argmax(1)).sum().item()
# 清除状态
functional.reset_net(model)
acc_train /= len(train_dataset)
loss_train_list.append(loss_train)
acc_train_list.append(acc_train)
print('loss_train:', loss_train)
print('acc_train:{:.2%}:'.format(acc_train))
# 模型测试
with torch.no_grad():
acc_test = 0
for x, y in test_loader:
f_out = torch.zeros((y.shape[0], 10))
# 逐步传播
for t in range(T):
encoded_x = encoder(x.reshape(-1,784))
f_out += model(encoded_x)
f_out /= T
loss = loss_function(f_out, y)
acc_test += (f_out.argmax(1) == y.argmax(1)).sum().item()
functional.reset_net(model)
acc_test /= len(test_dataset)
acc_test_list.append(acc_test)
print('acc_test:{:.2%}'.format(acc_test))
end_time = time.time()
print('Time:{:.1f}s'.format(end_time - start_time))
训练结果:
Epoch:10
loss_train: 0.8223596904426813
acc_train:91.10%
acc_test:90.24%
Time:123.3s
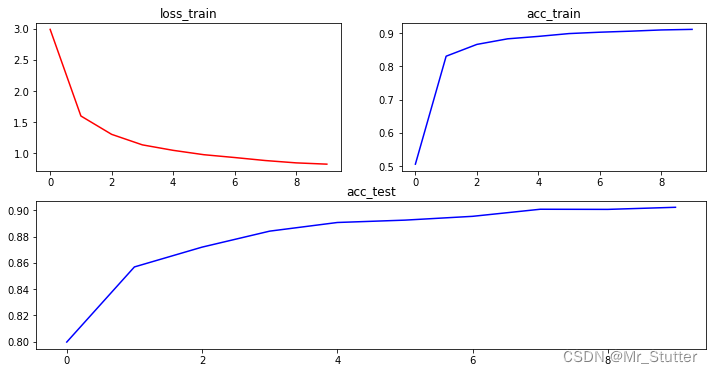
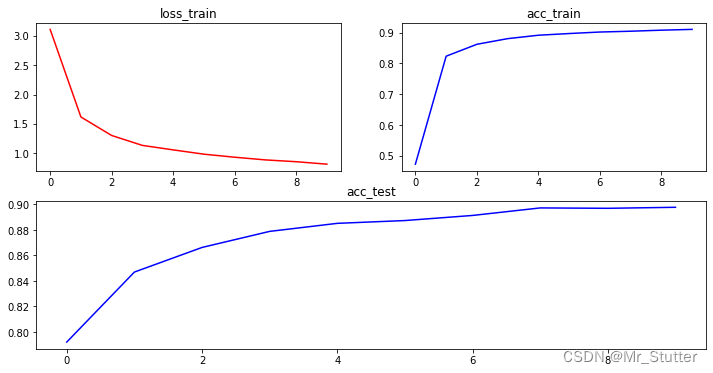
(6)显示损失值与准确率变化
fig1 = plt.figure(1, figsize=(12, 6))
ax1 = fig1.add_subplot(2, 2, 1)
ax1.plot(loss_train_list, 'r-')
ax1.set_title('loss_train')
ax2 = fig1.add_subplot(2, 2, 2)
ax2.plot(acc_train_list, 'b-')
ax2.set_title('acc_train')
ax3 = fig1.add_subplot(2, 1, 2)
ax3.plot(acc_test_list, 'b-')
ax3.set_title('acc_test')
plt.show()
训练结果:
(7)结果预测
选取一个数据,观察各神经元的膜电位变化与输出情况
# 设置监视器
for m in model.modules():
if isinstance(m, neuron.LIFNode):
m.store_v_seq = True
monitor_o = monitor.OutputMonitor(model, neuron.LIFNode)
monitor_v = monitor.AttributeMonitor('v',
pre_forward=False,
net=model,
instance=neuron.LIFNode)
print('model:', model)
print('monitor_v:', monitor_v.monitored_layers)
print('monitor_o:', monitor_o.monitored_layers)
# 选择一组输入
x, y = test_dataset[0]
f_out = torch.zeros((y.shape[0], 10))
with torch.no_grad():
# 逐步传播
for t in range(T):
encoded_x = encoder(x.reshape(-1,784))
f_out += model(encoded_x)
functional.reset_net(model)
label = y.argmax().item()
pred = f_out.argmax().item()
print('label:{},predict:{}'.format(label, pred))
# 膜电位与输出可视化
# 膜电位变化
dpi = 100
figsize = (6, 4)
# 合并列表中的张量,删除多余维度,删除梯度信息
v_list = torch.stack(monitor_v['layer.1']).squeeze().detach()
visualizing.plot_2d_heatmap(array=v_list.numpy(),
title='Membrane Potentials',
xlabel='Simulating Step',
ylabel='Neuron Index',
int_x_ticks=True,
x_max=T,
figsize=figsize,
dpi=dpi)
# 神经元输出
s_list = torch.stack(monitor_o['layer.1']).squeeze().detach()
visualizing.plot_1d_spikes(spikes=s_list.numpy(),
title='Out Spikes',
xlabel='Simulating Step',
ylabel='Neuron Index',
figsize=figsize,
dpi=dpi)
预测结果:
model: SNN(
(layer): Sequential(
(0): Linear(in_features=784, out_features=10, bias=False)
(1): LIFNode(
v_threshold=1.0, v_reset=0.0, detach_reset=False, step_mode=s, backend=torch, tau=2.0
(surrogate_function): ATan(alpha=2.0, spiking=True)
)
)
)
monitor_v: ['layer.1']
monitor_o: ['layer.1']
label:7,predict:7
膜电位变化:
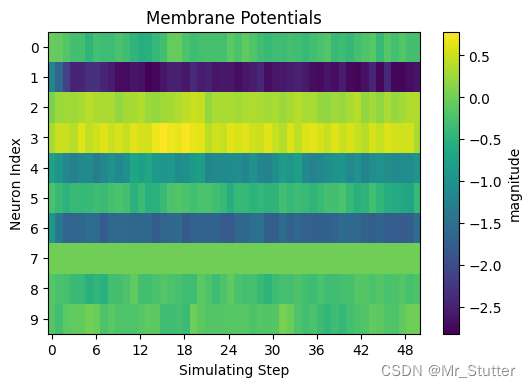
神经元输出:
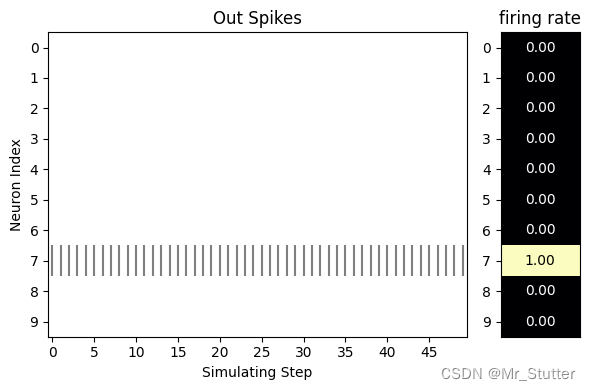
2、多步模式
将单步模式改为多步模式,需要修改以下部分:
(1)将神经元层的步进模式由’s’改为’m’
neuron.LIFNode(tau=2.0,
decay_input=True,
v_threshold=1.0,
v_reset=0.0,
surrogate_function=surrogate.ATan(),
step_mode='m',
store_v_seq=False)
(2)一次将所有时间步的数据全部输入
encoded_x = encoder(x).repeat(T,1,1))
f_out += model(encoded_x).sum(axis=0)
f_out /= T
(3)修改监视器监视的变量
monitor_v = monitor.AttributeMonitor('v_seq',
pre_forward=False,
net=model,
instance=neuron.LIFNode)
输出情况:
①训练结果
Epoch:10
loss_train: 0.8167978068813682
acc_train:91.06%:
acc_test:89.78%:
Time:145.1s
②网络结构
model: SNN(
(layer): Sequential(
(0): Linear(in_features=784, out_features=10, bias=False)
(1): LIFNode(
v_threshold=1.0, v_reset=0.0, detach_reset=False, step_mode=m, backend=torch, tau=2.0
(surrogate_function): ATan(alpha=2.0, spiking=True)
)
)
)
monitor_v: ['layer.1']
monitor_o: ['layer.1']
label:7,predict:7
③膜电位变化
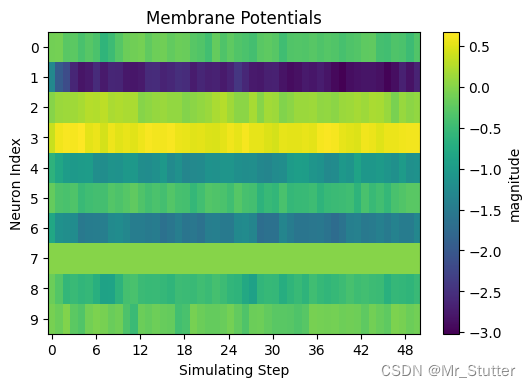
④神经元输出:
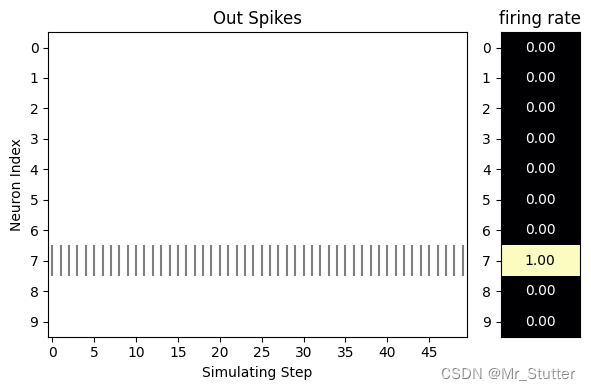
总结
使用梯度替代法进行反向传播时,使用可微的激活函数替代,避免脉冲的不可微;
使用编码器将输入编码为1/0脉冲序列;
将神经元层代替激活函数;
“在正确构建网络的情况下,逐层传播的并行度更大,速度更快”。但在此逐步传播比逐层传播略快一些。