强化学习的数学原理是由西湖大学赵世钰老师带来的关于RL理论方面的详细课程，本课程深入浅出地介绍了RL的基础原理，前置技能只需要基础的编程能力、概率论以及一部分的高等数学，你听完之后会在大脑里面清晰的勾勒出RL公式推导链条中的每一个部分。赵老师明确知道RL创新研究的理论门槛在哪，也知道视频前的你我距离这个门槛还有多远。

本笔记将会用于记录我学习中的理解，会结合赵老师的视频截图，以及PDF文档Book-Mathematical-Foundation-of-Reinforcement-Learning进行笔记注释，之后也会补充课程相关的代码样例，帮助大家理解

笔记合集链接（排版更好哦🧐）：《RL的数学原理》

记得点赞哟(๑ゝω╹๑)

前面章节贵在基础性，后面章节在于前沿性与实践性

• Chapter1：基本概念

• • 

• Chapter2：贝尔曼公式，重要的概念及工具，用以策略评价

• • 

• Chapter3：贝尔曼最优公式->最优策略，强化学习的最终目标就是求解最优策略， 需要把握两点：最优策略与最优状态价值。贝尔曼最优方程：1.不动点原理，2. 解决基础性问题，3. 提供求解贝尔曼方程的算法

• • 

• Chapter4： 你的第一类求解最优策略的算法：值迭代，策略迭代，Truncated policy（第三个是前两者的结合，亦或者说是前两者的一种积分情况）。以上三个算法都是迭代式的算法，都包含策略迭代与值迭代，在实践中不断迭代，从而获得最优策略。未来所有的算法都是以此为基本逻辑。另外，以上都需要环境模型。

• • 

• Chapter5：蒙特卡洛是最简单，也是唯一不需要模型的算法，需要明确没有模型的情况下，我们的训练目标是什么，以及我们所拥有的是什么：期望值（某种程度上可以理解为平均值），采样数据。模型与数据必有其一才可学习。你的第一类求解无模型的RL的算法：1. MC Basic（策略迭代数据版，效率特别低）, 2. MC Exploring Starts, 3.MC ϵ-greedy

• • 

• Chapter6：随机近似理论，估计随机变量的期望， 两种估计的方法：1.无增量的想法，需要对所有采样的结果都获取到之后求平均，获得近似，2. 有增量的想法，先对其有一个不准确的估计，每次获得采样后，不断更新估计。三种算法：1. Robbins-Monro（RM）算法,2. Stochastic gradient descent(SGD)随机梯度下降,3. SGD,BGD批量下降,MBGD小批量梯度下降三者之间的比较。

• • 

• Chapter7：时序差分方法，1. 用TD方法计算state value（前面使用了蒙特卡洛、模型等方法计算），2. Sarsa：用TD思想学习动作价值，3. Q-learing：用TD直接计算最优动作价值，因此是off-policy离线策略。Behaviour Policy 与 Target Policy 如果二者相同，那就是On-policy，反之就是Off-policy（可以从先前别的策略学习到的数据为我所用）

• • 

• Chapter8：从之前的邻接矩阵形式，迈入了函数表达式，使用近似函数模拟的方式求解状态价值：明确目标函数，求梯度，使用梯度上升或梯度下降进行优化。模型应用中，值函数的更新是通过真实值和函数值之差的绝对值来评判。与时序差分算法的多种结合。利用了神经网络所具有的优秀函数拟合能力，发展产生了深度强化学习。

• • 

• Chapter9：从Value-based迈入了policy-based，他们的区别在于后者是直接使用函数拟合，并且直接改变优化策略：明确目标函数，求梯度，使用梯度上升或梯度下降进行优化。

• • 

• Chapter10：结合Value-based（Critic）和policy-based（Actor）

• • 

课程是否适合你？

本课程是原理部分，偏向于用数学原理来描述问题，能够更全面更完整理解，只有深刻理解原理，才能有所创新

0节：课程介绍

1、Why this course？

• Reinforcement learning:An introduction.强化学习界的圣经（广泛引用，但是数学内容不多，对深入学习不算友好，同时会有高级知识提前出现在基础内容中，导致学习不太友好）
• 一大类书籍都偏向于通过文字描述，通过直观解释来介绍，另一大类又太过数学化，需要极强的专业背景，中间存在一个Gap等待被填充
• 我们希望从本质去回答去回答算法设计的逻辑，将数学控制在合理的水平，既能清晰展现原理，又不会过于晦涩
• 建议大家循序渐进，按照章节进行学习

2、The story of Alphago

3、Brief history of rl

DQN：RL与deep RL的分界线

Q-learning：一种时序差分算法

4、Details of this course

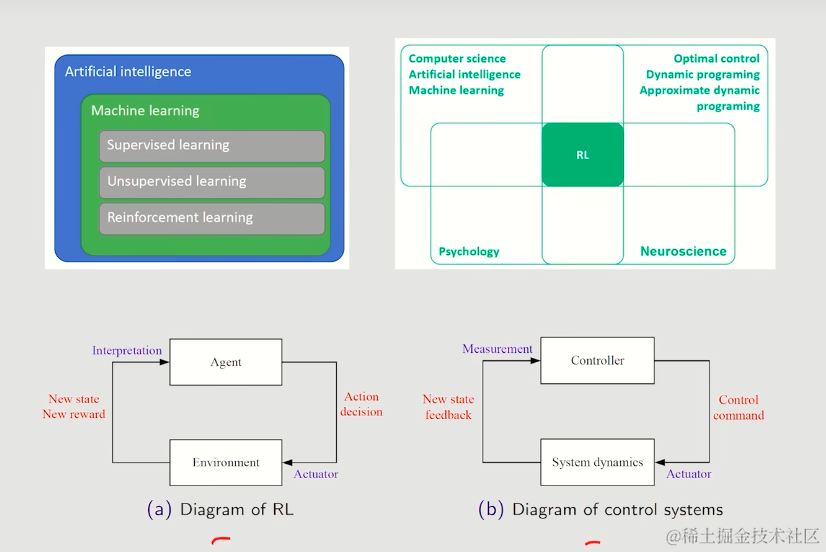
强化学习与监督学习、半监督学习并列属于ML，其有着广泛地交叉应用领域，并在控制方向上也有着重大作用