目录
- 1. 高斯混合分布
- 2. Mean-Shift算法
- 3. EM算法
- 4. 数据聚类
- 5. 源码地址
1. 高斯混合分布
在高斯混合分布中,我们假设数据是由多个高斯分布组合而成的。每个高斯分布被称为一个“成分”(component),这些成分通过加权和的方式来构成整个混合分布。
高斯混合分布的公式可以表示为:
p ( x ) = ∑ i = 1 K π i N ( x ∣ μ i , Σ i ) p(x) = \sum^K_{i=1} \pi_i N(x|\mu_i, \Sigma_i) p(x)=i=1∑KπiN(x∣μi,Σi)
其中:
- p ( x ) p(x) p(x)是观测数据点 x x x的概率密度函数,
- K K K是高斯分布的数量,
- π i \pi_i πi是第 i i i个高斯分布的混合系数,满足 ∑ i = 1 K π i = 1 \sum^K_{i=1} \pi_i = 1 ∑i=1Kπi=1,
- μ i \mu_i μi是第 i i i个高斯分布的均值向量,
- Σ i \Sigma_i Σi是第 i i i个高斯分布的协方差矩阵。
为了简单呈现结果,我们选取
K
=
2
K=2
K=2个高斯分布。下图为一个高斯混合分布的采样散点图,其中两个高斯分布的
μ
i
\mu_i
μi分别为
[
0
,
0
]
,
[
5
,
5
]
[0,0], [5,5]
[0,0],[5,5],协方差矩阵均为:
[
1
0
0
1
]
\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
[1001]

2. Mean-Shift算法
Mean-Shift是一种非参数化的密度估计和聚类算法,用于将数据点组织成具有相似特征的群集。它是一种迭代算法,通过计算数据点的梯度信息来寻找数据点在特征空间中的密度极值点,从而确定聚类中心。
算法的核心思想是通过不断地更新数据点的位置,将它们移向密度估计函数梯度的最大方向,直到达到收敛条件。具体来说,Mean-Shift算法包括以下步骤:
- 初始化:选择一个数据点作为初始聚类中心,或者随机选择一个点作为初始中心。
- 确定梯度向量:对于每个数据点,计算其与其他数据点之间的距离,并根据一定的核函数(如高斯核)计算梯度向量。梯度向量的方向指向密度估计函数增加最快的方向。
- 移动数据点:将每个数据点移动到梯度向量的方向上,即向密度估计函数增加最快的方向移动一定的步长。
- 更新聚类中心:对于移动后的每个数据点,重新计算它们周围数据点的梯度向量,并更新它们的位置。重复这个过程直到达到收敛条件,比如聚类中心的移动距离小于某个阈值。
- 形成聚类:最终,根据收敛后的聚类中心,将数据点分配到最近的聚类中心,形成最终的聚类结果。
Mean-Shift算法的优点是不需要事先指定聚类的个数,且能够自适应地调整聚类中心的数量和形状。它在处理非线性和非凸形状的数据集时表现出良好的聚类效果。然而,该算法对于大规模数据集的计算复杂度较高,且对初始聚类中心的选择敏感。Mean-Shift算法的具体实现见代码片:
class MeanShift:
def __init__(self, bandwidth=1.0, max_iterations=100):
self.min_shift = 1
self.n_clusters_ = None
self.cluster_centers_ = None
self.labels_ = None
self.bandwidth = bandwidth
self.max_iterations = max_iterations
def euclidean_distance(self, x1, x2):
return np.sqrt(np.sum((x1 - x2) ** 2))
def gaussian_kernel(self, distance, bandwidth):
return (1 / (bandwidth * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((distance / bandwidth) ** 2))
def shift_point(self, point, data, bandwidth):
shift_x = 0.0
shift_y = 0.0
total_weight = 0.0
for i in range(len(data)):
distance = self.euclidean_distance(point, data[i])
weight = self.gaussian_kernel(distance, bandwidth)
shift_x += data[i][0] * weight
shift_y += data[i][1] * weight
total_weight += weight
shift_x /= total_weight
shift_y /= total_weight
return np.array([shift_x, shift_y])
def fit(self, data):
centroids = np.copy(data)
for _ in range(self.max_iterations):
shifts = np.zeros_like(centroids)
for i, centroid in enumerate(centroids):
distances = cdist([centroid], data)[0]
weights = self.gaussian_kernel(distances, self.bandwidth)
shift = np.sum(weights[:, np.newaxis] * data, axis=0) / np.sum(weights)
shifts[i] = shift
shift_distances = cdist(shifts, centroids)
centroids = shifts
if np.max(shift_distances) < self.min_shift:
break
unique_centroids = np.unique(np.around(centroids, 3), axis=0)
self.cluster_centers_ = unique_centroids
self.labels_ = np.argmin(cdist(data, unique_centroids), axis=1)
self.n_clusters_ = len(unique_centroids)
3. EM算法
EM算法是一种迭代的数值优化算法,用于求解包含隐变量的概率模型参数的最大似然估计。它在统计学和机器学习领域被广泛应用,尤其在聚类问题中有着重要的应用。其基于观测数据和隐变量之间的概率模型,通过交替进行两个步骤:E步骤(Expectation Step)和M步骤(Maximization Step)来迭代地优化模型参数。下面是EM算法的基本步骤:
- 初始化:选择一组初始参数来开始迭代过程。
- E步骤:根据当前的参数估计,计算隐变量的后验概率,即给定观测数据下隐变量的条件概率分布。
- M步骤:使用在E步骤中计算得到的后验概率,对参数进行更新,以最大化对数似然函数。
- 重复步骤2-3至收敛:重复执行E步骤和M步骤,直到参数的变化很小或满足收敛条件。
在聚类问题中,EM算法可以用于估计混合高斯模型的参数,从而实现数据的聚类。EM算法在聚类中的应用优点是能够处理具有隐变量的概率模型,适用于灵活的聚类问题。然而,EM算法对于初始参数的选择敏感,可能会陷入局部最优解,并且在处理大规模数据集时可能会面临计算复杂度的挑战。EM算法(包含正则化步骤)的具体实现见代码片:
class RegularizedEMClustering:
def __init__(self, n_clusters, max_iterations=100, epsilon=1e-4, regularization=1e-6):
self.labels_ = None
self.X = None
self.n_features = None
self.n_samples = None
self.cluster_probs_ = None
self.cluster_centers_ = None
self.n_clusters = n_clusters
self.max_iterations = max_iterations
self.epsilon = epsilon
self.regularization = regularization
def fit(self, X):
self.X = X
self.n_samples, self.n_features = X.shape
self.cluster_centers_ = X[np.random.choice(self.n_samples, self.n_clusters, replace=False)]
self.cluster_probs_ = np.ones((self.n_samples, self.n_clusters)) / self.n_clusters
# EM
for iteration in range(self.max_iterations):
# E-step
prev_cluster_probs = self.cluster_probs_
self._update_cluster_probs()
# M-step
self._update_cluster_centers()
delta = np.linalg.norm(self.cluster_probs_ - prev_cluster_probs)
if delta < self.epsilon:
break
self.labels_ = np.argmax(self.cluster_probs_, axis=1)
def _update_cluster_probs(self):
distances = np.linalg.norm(self.X[:, np.newaxis, :] - self.cluster_centers_, axis=2)
# Calculate the cluster probabilities with regularization
numerator = np.exp(-distances) + self.regularization
denominator = np.sum(numerator, axis=1, keepdims=True)
self.cluster_probs_ = numerator / denominator
def _update_cluster_centers(self):
self.cluster_centers_ = np.zeros((self.n_clusters, self.n_features))
for k in range(self.n_clusters):
self.cluster_centers_[k] = np.average(self.X, axis=0, weights=self.cluster_probs_[:, k])
def predict(self, X):
distances = np.linalg.norm(X[:, np.newaxis, :] - self.cluster_centers_, axis=2)
return np.argmin(distances, axis=1)
4. 数据聚类
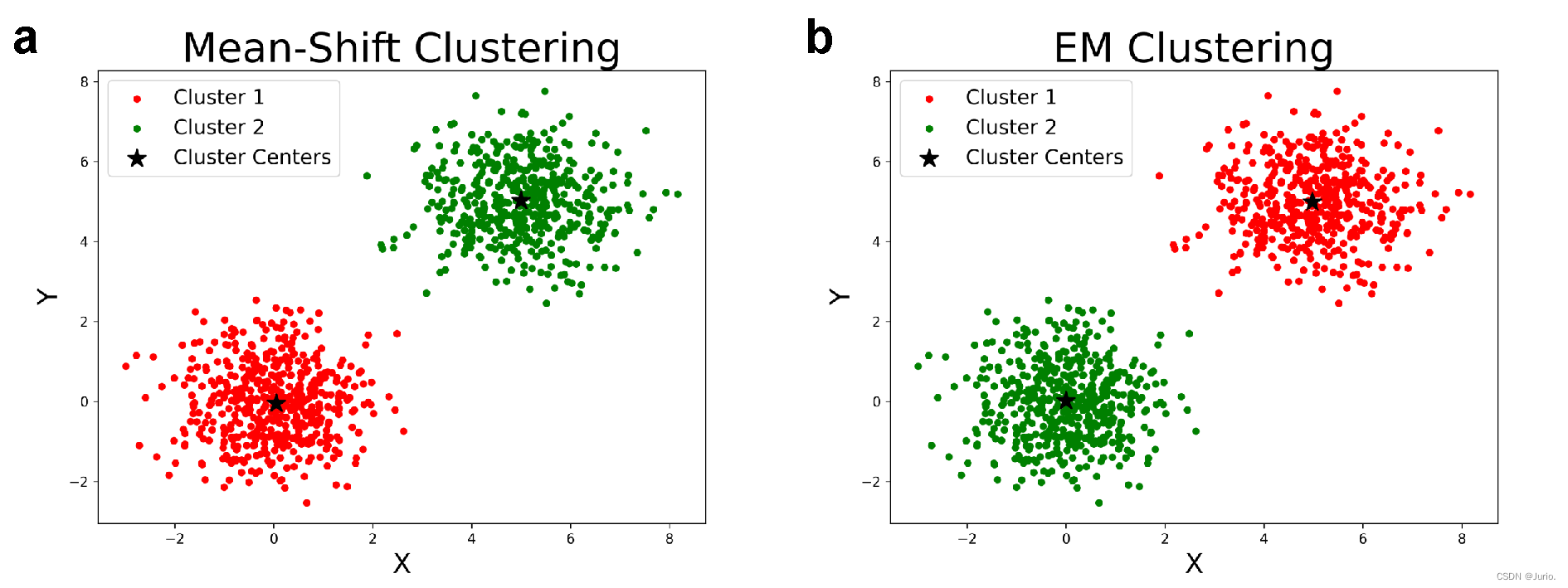
Mean-Shift和EM算法的聚类结果分别如图2的a-b子图所示,由于MoG比较简单,两种算法均可以合理且完整地实现聚类,聚类中心也没有显著差异。
5. 源码地址
如果对您有用的话可以点点star哦~
https://github.com/Jurio0304/cs-math/blob/main/hw3_clustering.ipynb
https://github.com/Jurio0304/cs-math/blob/main/func.py