经典机器学习算法—

Pagerank介绍

背景介绍

中心思想

一、量化重要性

三大指标

1、数量指标

2、质量指标

3、稀释指标

二、实际应用简化为理论模型

PageRank公式

手动预测网站的重要度

马尔可夫矩阵预测网站的重要度

两个方法的联系

PageRank算法存在的问题

一、Dead Ends问题

问题描述

出现原因及解释

图解示例

解决方法：Teleport

二、Spider Traps问题

问题描述

出现原因及解释

图解示例

编辑

解决方法

PageRank算法问题解决总结

PageRank代码实现

导包解决法

手搓代码版

一、随机有向图的生成

二、根据有向图生成马尔科夫矩阵

三、利用马尔科夫矩阵计算PR值

总结

Pagerank介绍

背景介绍

PageRank 算法由 Google 创始人 Larry Page 在斯坦福读大学时提出，又称 PR——佩奇排名。主要针对网页进行排名，计算网站的重要性，优化搜索引擎的搜索结果。PR 值是表示其重要性的因子

中心思想

实现网站排名的重点及难点就在于对网站重要性的衡量。一旦确认了网站的重要性，那么搜索引擎就可以根据网站的重要性对搜索结果的网站进行排名。

PR算法核心就在于：一、量化重要性；二、实际应用简化为理论模型

一、量化重要性

为了理解佩奇算法的核心思想——如何衡量一个网页的重要性，我们需要提前理解下面的一个观点（划重点）：

1、每个网页本身无重要性，网页重要性靠其他网页提供

2、所有指向该网页的其他网页，反映该网页的重要性（避开对网页内容的衡量）

三大指标

拉里佩奇老师在巧妙避开对网页内容衡量来确认重要性的陷阱后，提出了三个具体思考角度来衡量一个网页的重要性

1、下图网页大小与其重要性相挂钩，网页越大代表其越重要

2、不同图的大小重要标准相同，可以结合着看

1、数量指标

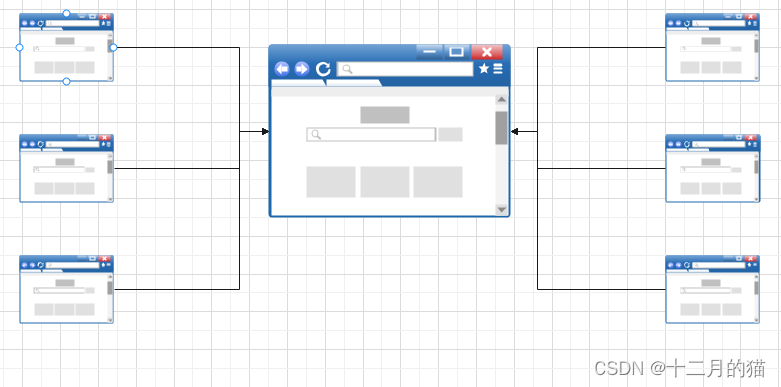
当在网页模型图中，一个网页接受到的其他网页指向的入链（in-links）越多，说明该网页越重要。换句话说，越多的网页引用了该网页，那么该网页就越重要（因为它影响力越大）

2、质量指标

当一个质量高的网页指向（out-links）一个网页，说明这个被指的网页重要。例如：一个诺贝尔奖的得主说你的网页好，和一个普通人说你的网页好所提供的影响力是不一样的。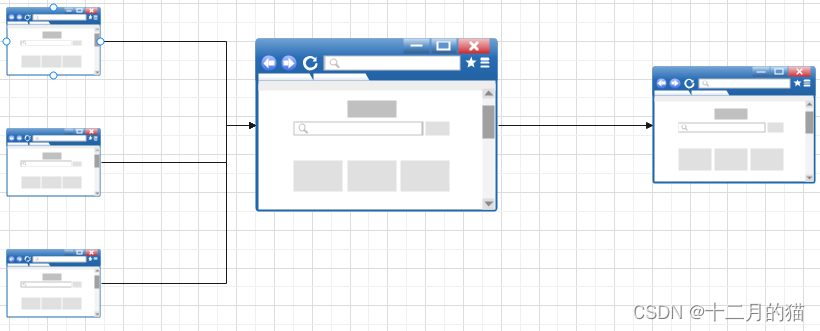

（图中右边网页，重要性就比左边的网页要高，因为一个重要性高的网页指向它）

3、稀释指标

假如一个质量很高的网页指向你的网页，但是同时也指向了很多其他的网页，那么此时这个网页能够给你的网页提供的重要性增幅也是有限的，重要性会被稀释掉。因为基于随机冲浪者理论，用户在浏览时有很大概率会通过这个高质量网站“冲浪”到其他它所指向的网站，而不是你的网站

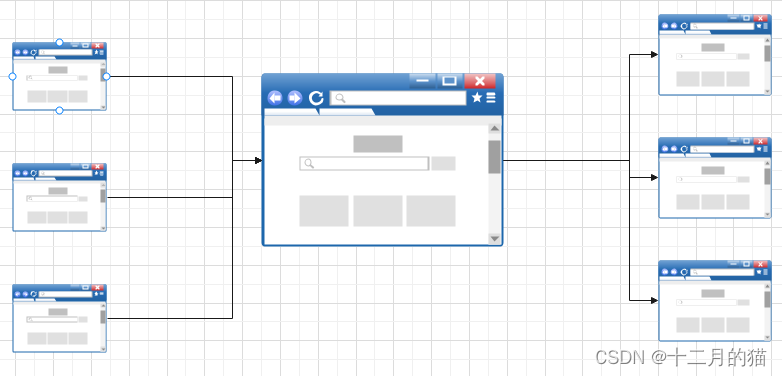
（图中右边网页相比于上一张图中最右边网页较小，因为中间网页的重要性被稀释为了三份）

二、实际应用简化为理论模型

有了上面的三大衡量指标后，如何简化生活中的实际问题为数学理论的模型也是相当关键的。数学建模的过程也意味着，我们必须要：1、抽象、提炼问题的本质；2、简化问题的表象

在这里，PageRank算法，将网页以及他们之间的关系抽象为有向图。可以利用有向图的知识来求解

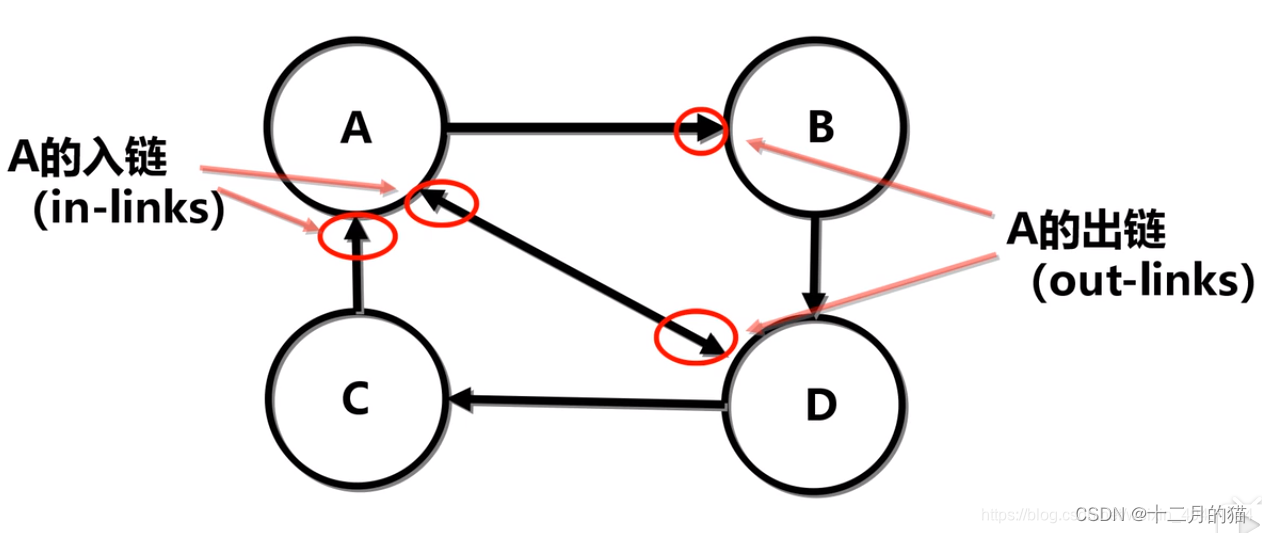
（上图每个节点代表一个网站，连接表示网站间的链接关系）

最终要实现的机器学习算法：给予网站关系有向图，算法能够自我学习这个关系图然后预测网站最终的重要度

PageRank公式

$P R(a)_{i+1}=\sum_{i=0}^{n}{\frac{P R(T i)_{i}}{L(T i)}}$

PR(a)：a节点（a网站）的重要性
i+1：第i+1次迭代，算法循环次数
PR(Ti)：指向a节点的其他节点的PR值
L(Ti)：指向a节点的其他节点的总出链数

1、PR（Ti）就体现了质量指标

2、 $\sum$ 就体现了数量指标

3、除L（Ti）就体现了稀释指标

手动预测网站的重要度

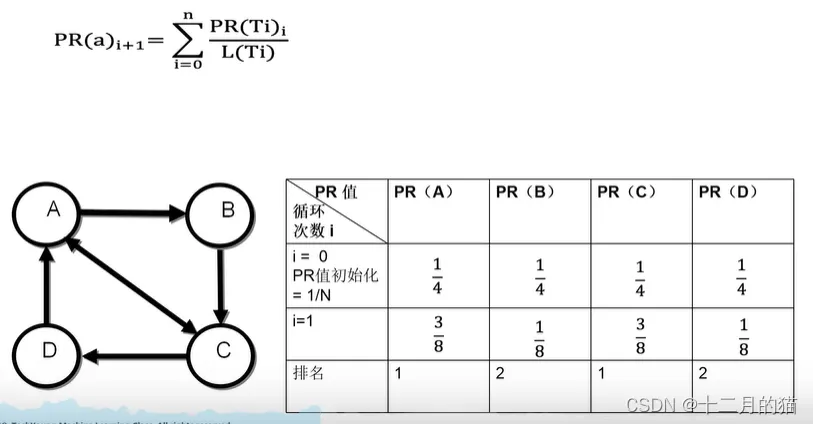
具体计算过程（拿一个例子）：

$i={\bf1},P R(C)_{\mathrm{{1}}}=\frac{P R(A)_{0}}{L(A)}+\frac{P R(B)_{0}}{L(B)}=\frac{{\textstyle\frac{1}{4}}}{2}+\frac{{\textstyle\frac{1}{4}}}{1}=\frac{3}{8}$

关键点：

1、一开始要给每个节点初始重要值：1/N（N为节点总数）

2、每一轮都是按顺序给所有节点更新重要值，更新是拿前一轮的值

3、直到所有节点重要值不变为止

按照公式定义来计算PR值存在一个问题，就是我们需要一步步自己去迭代实现。拉里佩奇便要思考一个可以实现让计算机自己去一步步计算，最终输出结果的智能算法

马尔可夫矩阵预测网站的重要度

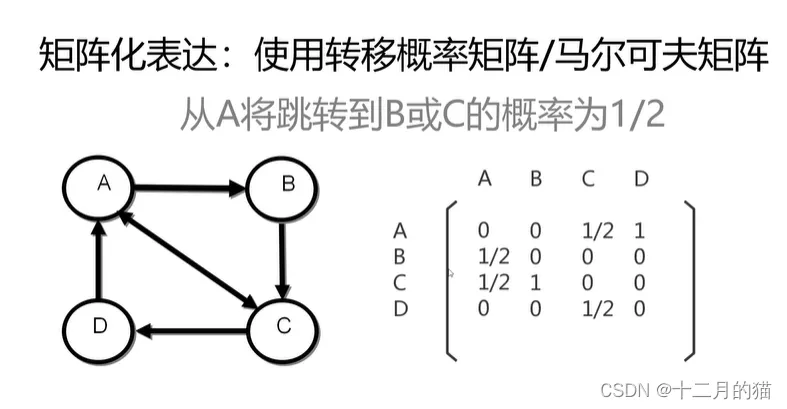
矩阵关键点：

1、列表示出链：例如第一列就表示A出链到ABCD各个点的概率值

2、行表示入链：例如第一行就表示ABCD入链到A的概率值

计算得到：

两个方法的联系

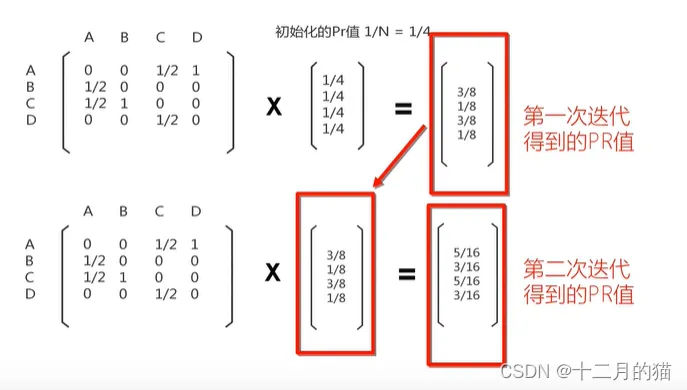
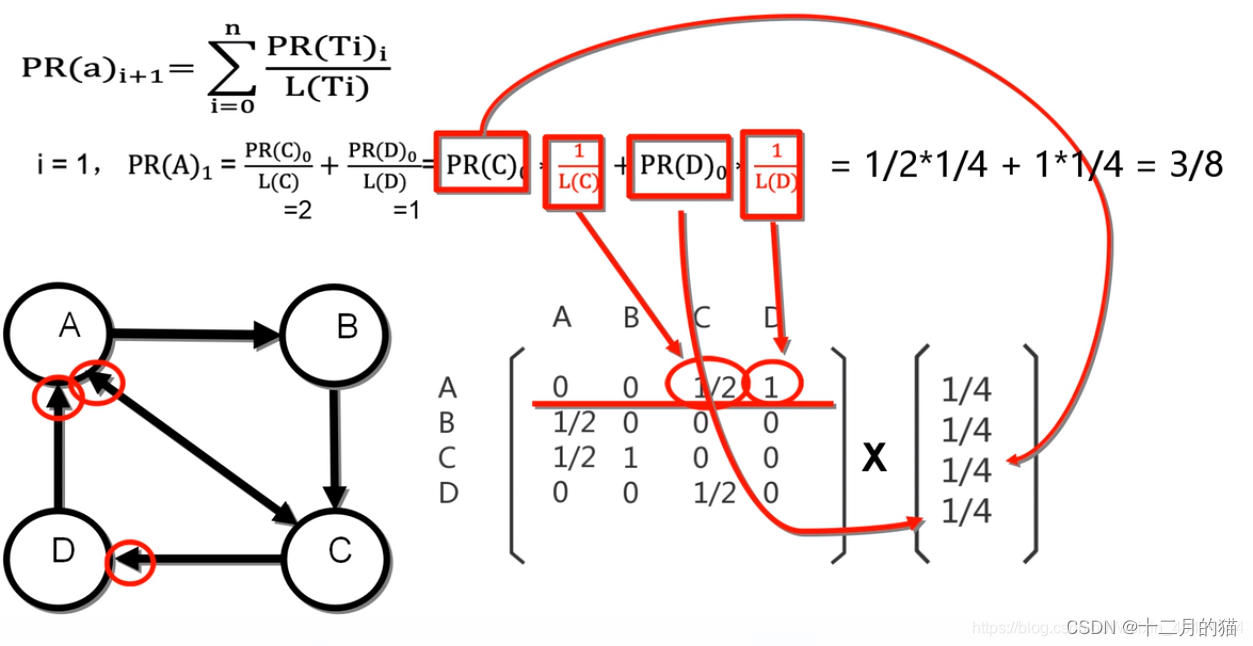
理解关键点：

1、矩阵*向量=矩阵行 *向量作为结果向量的行

2、联系三个含义：矩阵行的含义，向量的含义，结果向量的含义

PageRank算法存在的问题

PageRank算法主要存在两个问题：一、Dead Ends问题；二、Spider Traps问题。这两个问题都是在特殊情况才会出现，但是一出现便会让我们的佩奇排序算法无法执行

Spider traps问题和Dead ends问题是PageRank算法中两种不同的情况，它们都会影响链接结构的平衡性。具体来说：

Dead ends问题：指的是某些节点没有任何出边，即它们不会将PageRank值传递给其他页面。这会导致这些页面积累较高的PageRank值，因为它们只接收来自其他页面的值而不向外传递。
Spider traps问题：是指一些网页故意设计成只有入链而几乎没有或没有出链，有时还包含指向自己的链接，即自环。这种结构会导致PageRank值在这些“陷阱”网页上积累，使得它们获得异常高的排名，从而影响整个网络的链接结构。

一、Dead Ends问题

问题描述

在多次迭代后，所有网站的重要性都转变为0

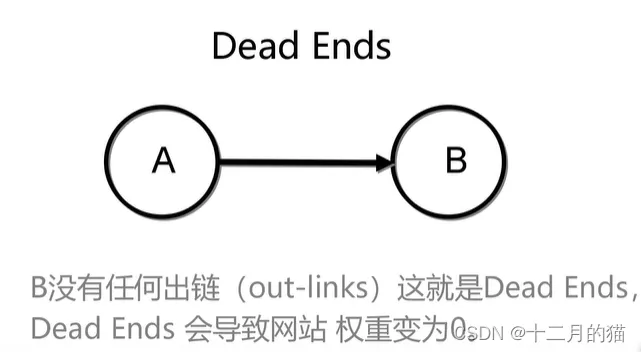
出现原因及解释

原因：由于网络中某些节点没有指向其他节点的出链，导致链接结构中断

解释：

1、利用佩奇算法确定网站的重要性可以理解为：让一个小虫子在网站间不停且随机地爬，它爬到哪个网站的次数最多，则这个网站的重要性就越高

2、此时假如其中一个网站没有出链，那么当小虫子爬到该网站时便无法离开，此时其他网站就无法被小虫子爬到，因此重要性都会迭代为0。最后由于该网站本身也是依靠其他网站的重要性来确定自身重要性的，所以该网站的重要性也将变为0，即虫子无法运动导致爬虫死亡

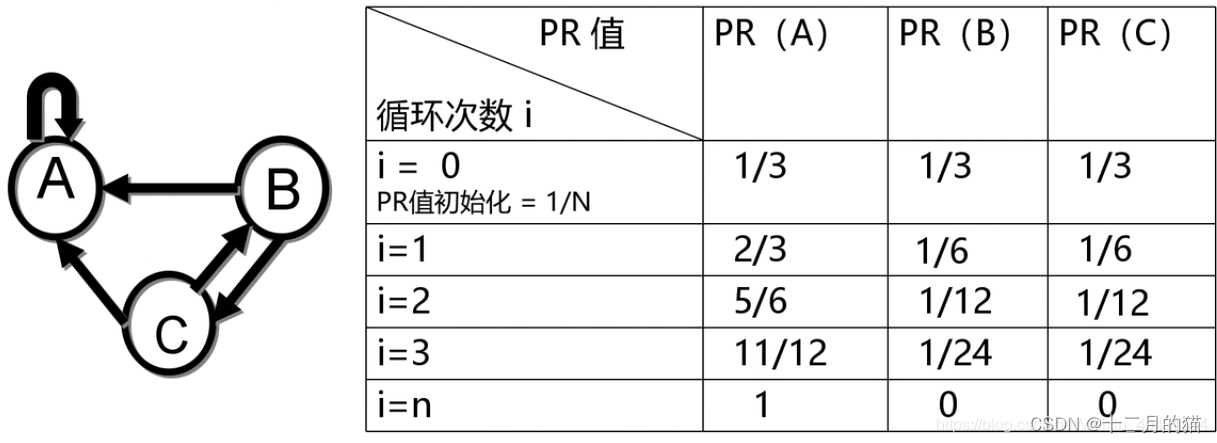
图解示例

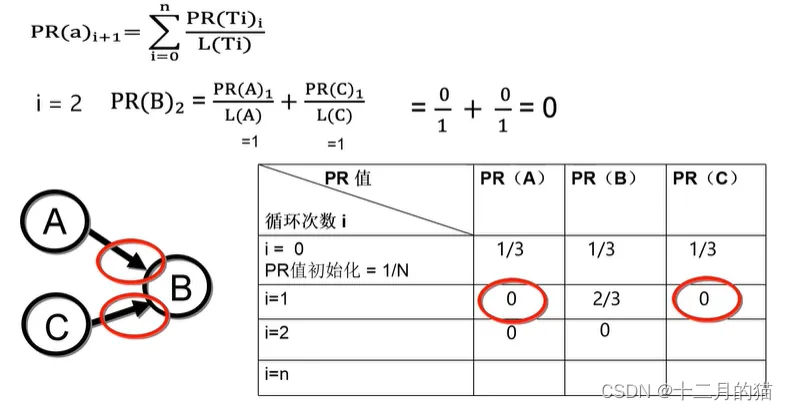
使用马尔科夫矩阵快速计算PR值：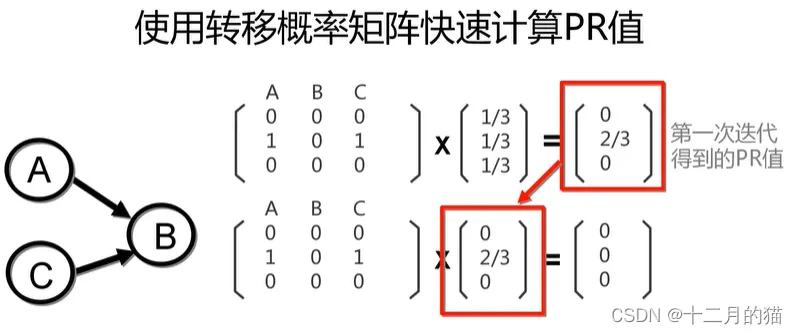

解决方法：Teleport

既然问题出现的原因是存在一个没有出链的网站，那么我们在PageRank算法执行前对有向图矩阵进行检查。如果存在这种不合要求的有向图矩阵，那么我们便执行下面的操作：

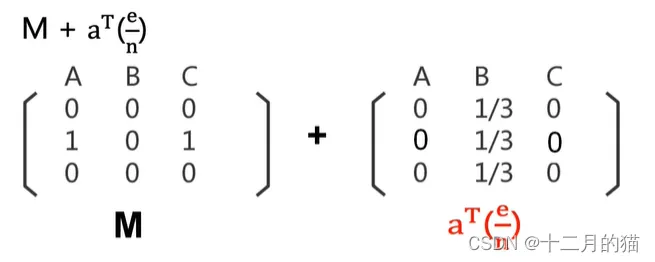
关键点：

1、引入了“传送”（teleport）机制。当冲浪者遇到一个没有出链的页面时，1/n的概率随机跳转到任意一个页面（假设总共能跳转的页面有n个）

二、Spider Traps问题

问题描述

Spider traps问题是PageRank算法中的一种现象，它指的是某些网页故意设计成只有入链以及指向自己的出链，即自环，以此来提升网页的重要性

出现原因及解释

原因：网页只有入链以及指向自己的出链

解释：

1、利用佩奇算法确定网站的重要性可以理解为：让一个小虫子在网站间不停且随机地爬，它爬到哪个网站的次数最多，则这个网站的重要性就越高

2、当出现这种问题，小虫子走到Traps节点时，由于该节点没有出链只有自环。所有小虫子会在这个节点不停的循环走，这就会导致该节点的重要性不停提高直到1，而其他节点的重要性降低到0

图解示例

按照这个规律，我们在多次循环之后，会发现这个模型中 A 的 PR 值都会归于 1，其他归为 0

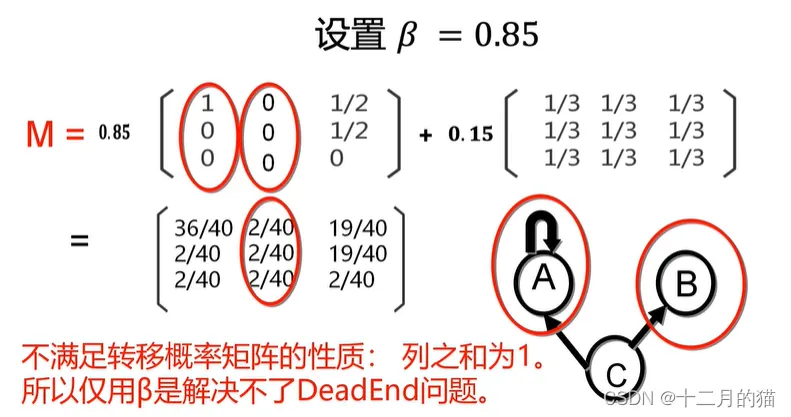
解决方法

1、选择概率 $\beta$ 为跟随出链，正确打开网页的概率。1- $\beta$ 为随机打开网页的概率

2、按照概率 $\beta$ 加权分配这个概率矩阵

PageRank算法问题解决总结

1、两个问题的解决都利用：修正M矩阵

2、前者直接加上修正矩阵，使得不存在全为0的列即可

3、后者需要对M矩阵进行等比例缩小，再加上加权处理后的修正矩阵。如此，才能让矩阵中不再存在为1的值

4、Spider Traps的解决方法不可以用于Dead ends。原因如下：

5、 Dead ends的解决方法不能用于Spider Traps，原因是直接加上一个矩阵，Spider Traps为1的值仍然无法解决

6、两个方法的限制点：a. 列之和为1；b. 不能存在为1的值

7、 $\beta$ 值越大表明按照链接正常跳转的概率越大，这也意味这爬虫的移动会在相邻节点间进行，模型收敛速度变慢；反之值越少，随机链接访问的概率越大，这样意味着模型各网站的重要性相差越近，模型收敛速度越快

PageRank代码实现

导包解决法

import matplotlib.pyplot as plt
import networkx as netx  # 网络图库：生成构造网络图，并对网络图进行各类分析
import random

random.seed(42)  # 设置随机数种子,让结果可以复现
diGraph = netx.DiGraph()  # 生成有向图
diGraph.add_nodes_from(range(0, 100))  # range生成一个可迭代对象（迭代器：1、访问工具，本身不是具体的数据类型，可以对各种数据类型进行迭代；2、动态生成值，在每一次运行时动态加载到内存）
for i in range(100):
    j = random.randint(0, 100)
    k = random.randint(0, 100)
    diGraph.add_edge(k, j)

# 绘图
netx.draw(diGraph, with_labels=True)
plt.show()

# 计算并生成PR值
prValue = netx.pagerank(diGraph, max_iter=500, alpha=0.85)  # 生成的对象是一个字典类型

# 对PR值进行排序
prValue_list = list(prValue.items())  # 利用items（视图元组，不是实际元组）将字典转为元组，再用list将元组转为列表（可迭代访问对象）

# 使用 sorted() 函数对 prValue_list 进行排序，按照值（即 PageRank 值）从大到小排序
sorted_prValue = sorted(prValue_list, key=lambda x: x[1], reverse=True)

print(sorted_prValue)

手搓代码版

代码可以分为三个部分：

1、随机有向图的生成；2、根据有向图生成马尔科夫矩阵；3、利用马尔科夫矩阵计算PR值

这里我创建一个Python项目——PageRank

项目下有四个子项目：graph_generate.py、matrix_generate.py、pagerank.py、main.py

一、随机有向图的生成

graph_generate.py子项目

import networkx as nx
import matplotlib.pyplot as plt

def get_init_pr(dg):
    """
    获得每个节点的初始PR值

    :param dg: 有向图
    """
    nodes_num = dg.number_of_nodes()
    for node in dg.nodes:
        pr = 1 / nodes_num
        dg.add_nodes_from([node], pr=pr)


def create_network():
    """
    创建有向图

    :return dg: 有向图
    """
    dg = nx.DiGraph()  # 创建有向图
    dg.add_nodes_from(['0', '1', '2', '3', '4'])  # 添加节点
    dg.add_edges_from([('1', '0'), ('2', '1'), ('3', '4'), ('4', '1'), ('3', '1')])  # 添加边

    get_init_pr(dg)

    return dg


def draw_network(dg):
    """
    可视化有向图

    :param dg: 有向图
    """
    fig, ax = plt.subplots()
    nx.draw(dg, ax=ax, with_labels=True)
    plt.show()

二、根据有向图生成马尔科夫矩阵

matrix_generate.py子项目

import numpy as np

def solve_ranking_leaked(adj_matrix):
    """
    解决Dead Ends问题（也称为排名泄露问题）
    :param adj_matrix: 邻接矩阵
    """
    col_num = np.size(adj_matrix, 1)  # 获得邻接矩阵列数

    row_num = 0  # 用来统计矩阵的行数（只有通过出度的问题检查才算）
    for row in adj_matrix:
        # 如果排名泄露，那么修改这个节点对每个节点都有出链
        if sum(row) == 0:  # 这个节点出度为0，表明它存在排名泄露问题
            for col in range(col_num):
                adj_matrix[row_num][col] = 1
        row_num += 1


def calc_out_degree_ratio(adj_matrix):
    """
    计算每个节点影响力传播的比率，即该节点有多大的概率把影响力传递给下一个节点
    公式：
        out_edge / n
        out_edge: 出边，即这个节点可以把影响力传递给下一个节点
        n: 这个节点共有多少个出度

    :param adj_matrix: 邻接矩阵
    """
    row_num = 0
    for row in adj_matrix:  # 每次都拿出一个行列表
        n = sum(row)  # 求该节点的所有出度
        col_num = 0
        for col in row:
            adj_matrix[row_num][col_num] = col / n  # out_edge / n
            col_num += 1

        row_num += 1


def create_matrix(dg):
    """
    通过有向图生成邻接矩阵
    :param dg: 有向图
    :return adj_matrix: 邻接矩阵
    """
    node_num = dg.number_of_nodes()

    adj_matrix = np.zeros((node_num, node_num))

    for edge in dg.edges:
        adj_matrix[int(edge[0])][int(edge[1])] = 1

    solve_ranking_leaked(adj_matrix)
    calc_out_degree_ratio(adj_matrix)
    # print(adj_matrix)
    return adj_matrix


def create_pr_vector(dg):
    """
    创建初始PR值的向量

    :param dg: 有向图
    :return pr_vec: 初始PR值向量
    """
    pr_list = []
    nodes = dg.nodes

    # 将初始PR值存入列表
    for node in nodes:
        pr_list.append(nodes[node]['pr'])

    pr_vec = np.array(pr_list)  # 将列表转换为ndarray对象

    return pr_vec

三、利用马尔科夫矩阵计算PR值

pagerank.py子项目

import numpy as np
import matplotlib.pyplot as plt

# 设置阻尼因子（跳转因子）防止Spider traps问题
alpha = 0.85  # 跳转因子


def draw(iter_list, pr_list):
    """
    绘制收敛图

    :param iter_list: 迭代次数列表
    :param pr_list: 每一个向量的值
    :return:
    """
    plt.plot(iter_list, pr_list)
    plt.show()


def pagerank(adj_matrix, pr_vec):
    """
    pagerank算法:
        V_{i+1} = alpha * V_i * adj + (1 - alpha) * E/ N
        （这个公式和上文介绍的略有不同，但是这两个是等价的）
         按照上文解决Spider Traps的方法，公式应该为：
                V_{i+1} = （alpha  * adj + ((1 - alpha) / N) * E）* V_i

    收敛条件:
        1. V_{i+1} == V_i
        2. 迭代次数200次

    就是说如果PR向量并没有发生改变，那么收敛结束，得到的PR值就是最终的PR值
    但是假设迭代次数过高后且未发生收敛，那么就会陷入死循环等，根据前人总结的经验，设置为迭代20次

    :param adj_matrix: 邻接矩阵
    :param pr_vec: 每个节点PR值的初始向量
    :return:
    """
    num_nodes = np.size(adj_matrix, 1)  # 获得矩阵列数(ie. 节点数)
    jump_value = (1 - alpha) / num_nodes  # 从其他页面跳转入所在页面的概率(标量)
    jump_vec = jump_value * np.ones(num_nodes)  # 向量化

    # iter_list = []
    # pr_list = []

    for n_iter in range(1, 201):
        pr_new = alpha * np.dot(pr_vec, adj_matrix) + jump_vec

        print("第{0}次迭代的PR值:{1}".format(n_iter, pr_new))

        # iter_list.append(n_iter)
        # pr_list.append(tuple(pr_new))

        if (pr_new == pr_vec).all():
            break
        # else:
        #     # 调试用
        #     test = pr_new - pr_vec

        pr_vec = pr_new

    # draw(iter_list, pr_list)

    print("迭代完成!")
    print("收敛值为:", pr_vec)

总结

PageRank 算法是现代数据科学中用于图链接分析的经典方法，最初由LarryPage 和Sergey Brin 在1996年提出。两位斯坦福大学研究生认为互联网上的链接结构能够反映页面的重要性，与当时基于关键词的搜索方法形成对比。这一独特观点不仅赢得了学术界的认可，也为后来创建的Google搜索引擎奠定了基础。

PageRank的核心思想基于有向图上的随机游走模型，即一阶马尔可夫链。描述了随机游走者如何沿着图的边随机移动，最终收敛到一个平稳分布。在这分布中，每个节点被访问的概率即为其PageRank值，代表节点的重要性。 PageRank是递归定义的，计算需要迭代方法，因为一个页面的值部分取决于链接到它的其他页面的值。尽管最初设计用于互联网页面，但PageRank已广泛应用于社会影响力、文本摘要等多个领域，展示了其在图数据上的强大实用性

撰写文章不易，如果文章能帮助到大家，大家可以点点赞、收收藏呀~

十二月的猫在这里祝大家学业有成、事业顺利、情到财来