在讲VTK的数据结构之前,我们先了解可视化数据的两个特征:离散性、有规则或无规则。
- 离散性。当我们使用计算机去表示我们的数据时,一般都是基于有限数量的点做信息的采样(或插值),因此可视化的数据是以一种离散的方式表示的。
- 有规则或无规则(也叫结构化或非结构化)。针对有规则的数据,不需要存储所有点的坐标,仅仅需要存起点、步长、点的个数(有的可能还需要知道方向),所有点的位置就能隐式的知道了,这样能节约内存空间。针对无规则的数据,它能在改变比较快的位置(例如拐角位置)表示比较稠密的信息而在变化不大的位置表示较少的信息,这样能给数据表示提供更多的自由。
下面我们就来看看,这些特征是如何塑造VTK的可视化数据模型的。
1 数据集(vtkDataSet)
具有组织结构和相关属性的数据对象形成数据集。
数据集的结构由两部分组成:拓扑结构和几何形状。拓扑是在确定的几何变换(旋转、偏移、缩放)之下一组不变的属性。几何形状是拓扑的实例化,它指定3D空间中的位置。例如,说一个多边形是“三角形”,指的是拓扑。提供点的坐标,指的是几何形状。
数据集的属性补充与几何形状和拓扑结构相关的信息,该信息可能是某点的温度或某个单元的惯性质量。
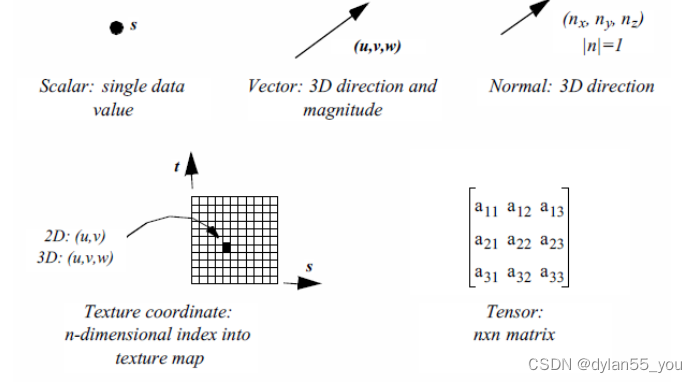
VTK中数据集由单元(cell)和点(point)组成。单元指的是拓扑,而点指的是几何形状。特定属性包括:scalars(标量)、vectors(向量)、normals(法向)、texture coordiantes(纹理坐标)、tensor(张量)。
单元(cell)类型
一个数据集由一个或多个单元组成,单元是可视化系统的基本组成部分。单元是通过指定类型与有序点列表的组合来定义的。有序列表,通常称为连通性(connectivity)列表,它与指定类型结合,隐式地定义了单元的拓扑结构。x-y-z点坐标定义了单元的几何形状。
虽然我们在三维空间定义点,但单元的拓扑维度可能会有所不同。Vertices(顶点),lines(线)、triangles(三角形),tetrahedra(四面体)分别是0维,1维,2维,3维拓扑结构的例子,它们被嵌入在几何空间中。单元可以是基本的和复合的。复合的单元由一个或多个基本的单元组成,而基本单元不能分解成其他基本单元类型的组合。例如三角带(triangle strip)由一个或多个以紧凑形式排列的三角形组成。三角带是复合单元,因为它可以分解成三角形,而三角形是基本单元。
可能的单元类型是无限的,在VTK中,每种单元类型都是根据应用需求选择的。我们已经看到了一些单元类型:顶点、线、多边形和三角带是如何表示几何形状的。其他单元类型,如四面体和六面体,在数值模拟中很常见。
单元类型分为线性、非线性或其他类型。
线性单元类型
线性单元的特征是线性,因此一维或更大维度单元的特征是直边,任何边都可以用两个顶点id(v1,v2)来表示。以下是目前在VTK中能找到的线性单元。
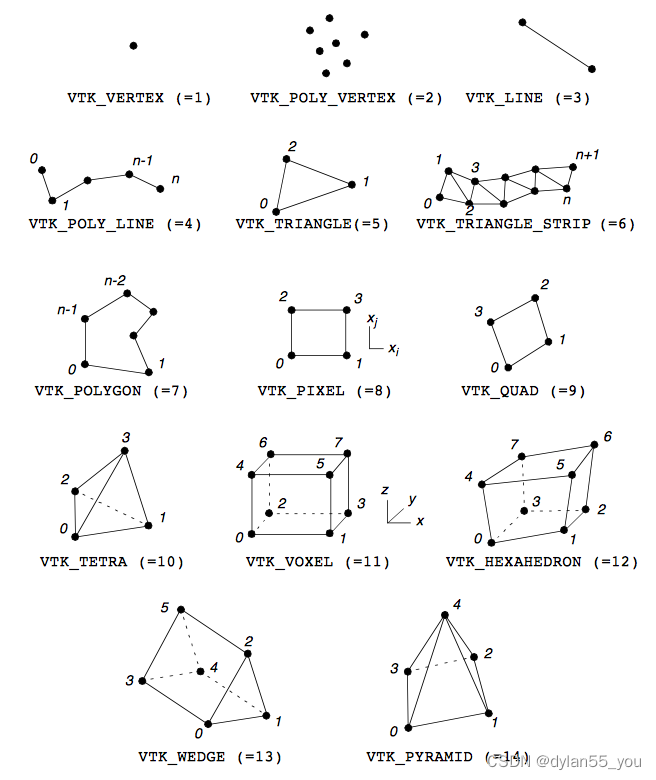
非线性单元类型
在数值分析中,通常使用非线性单元,即使用非线性基本函数的单元公式。这些基础函数通常由多项式组合而成。非线性单元提供更精确的插值函数和更好的近似曲线几何。以下是目前在VTK中能找到的非线性单元。

线性和非线性单元之间的一个显著区别是它们被各种可视化算法渲染和操作的方式不同。线性单元很容易转换为线性图元,然后由图形库进行处理。而非线性单元通常不被图形库直接支持。(非均匀有理B样条或NURBS系列是一个例外,即使这些通常也被图形库细分为线性图元)因此,可视化系统必须对非线性单元进行特殊处理。一些可能性包括:
- 将非线性单元细分为线性单元,然后对线性单元进行操作。
- 开发自定义渲染和可视化算法以直接对非线性单元进行操作。
- 在图形库中编写自定义渲染操作。
这些问题都是可视化研究中的热门话题。在VTK中,目前采用的是细分(tessellation)方法,因为一旦单元被细分,就可以用现有的线性算法进行处理。上述解决方案2和3的难点在于,创建新的渲染和可视化算法需要付出很大的努力,可能需要为每种类型的非线性单元提供不同的解决方案。方案1的难点在于,必须小心地进行细分,否则可能在可视化中引入不可接受的误差,或者单元被过度细分,则会产生过多的线性单元。
VTK使用下图这种固定的细分方法来细分非线性二次单元。由于插值的阶数较低,并且定义单元的点数较少,这通常适用于二次单元。
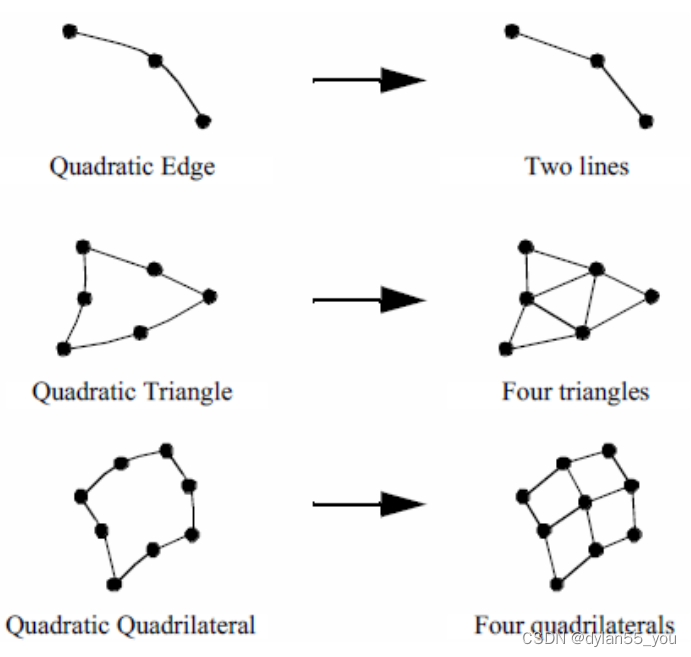
2 数据集类型
常见的数据集类型如下图所示:

多边形数据(Polygonal Data)
多边形数据集由顶点(vertices)、多顶点(polyvertices)、线(lines)、折线(polylines)、多边形(polygons)和三角带(triangle strips)组成。多边形数据的拓扑和几何形状是非结构化的,组成该数据集的单元在拓扑维度上有所不同。
多顶点、折线和三角形带单元是为了方便、压缩和性能而添加的,以三角带为例,它具有较高的性能,用三角形带表示n个三角形仅需要n+2个点,而传统表示则需要3n个点。此外,许多图形库可以以比三角形更高的速度渲染三角形带。
图像数据(Image Data)
图像数据由线元素(1D)、像素(2D)或体素(3D)组成。图像数据在几何形状和拓扑结构上都是规则(结构化)的,并且可以隐式表示,只需要数据维度、原点、数据间距和指定x,y和z方向上的点数。
图像数据集通常用于成像和计算机图形学。体(Volumes)通常有医学成像技术(例如断层扫描(CT)和磁共振成像(MRI))生成。
直线网格(Rectilinear Grid)
与图像数据一样,直线网格由像素(2D)或体素(3D)组成。虽然直线网格数据集的拓扑结构是规则的,但几何形状只是部分是规则的。也就是说,点沿坐标轴排列,但点之间的间距可能会有所不同。拓扑结构通过指定网格维度隐式表示。要获得特定点的坐标,必须适当组合三个列表的值。
结构化网格(Structured Grid)
结构化网格数据的拓扑结构和几何形状都是规则的。结构化网格的拓扑结构通过指定vector(nx, ny, nz)来隐式表示。结构化网格的组成单元是四边形(2D)或六面体(3D)。与图像数据一样,结构化网格具有自然坐标系,允许我们使用拓扑i-j-k坐标来引用特定点或单元。
结构化网格通常用于有限差分分析。有限差分是一种数值分析技术,用于近似偏微分方程的解。典型应用包括流体流动、传热和燃烧。
非结构化点(Unstructured Points)
非结构化点是空间中不规则分布的点。非结构化点数据集中没有拓扑,几何形状完全是非结构化的。使用顶点和多顶点单元来表示非结构化点。
非结构化网格(Unstructured Grid)
最普遍的数据集形式是非结构化网格。拓扑和几何形状都是完成非结构化的。任何单元类型都可以在非结构化网格中进行任意组合。因此,单元格的拓扑范围从0D(顶点、多顶点)到3D(四面体、六面体、体素)。在VTK中,任何数据集类型都可以表示为非结构化网格。我们通常只在绝对必要时才使用非结构化网格来表示数据,因为这种数据集类型需要最多的内存和计算资源来表示和操作。
3 属性数据(vtkDataSetAtrributes)
属性数据是与数据集关联的信息。此数据包括数据集几何形状和拓扑结构。属性数据通常与数据集的点或单元关联(例如vtkPointData和vtkCellData),但有时属性数据可能也分配给单元组件,例如边或面。属性数据也可以分配整个数据集(例如vtkFieldData),或一组单元或点。我们将此信息称为属性数据,是因为它是数据集结构的属性。典型的示例包括某个点的温度或速度、单元的质量。
属性数据通常被归类为特定类型(如下图)的数据。这些类别是针对常见数据形式而创建的。可视化算法也根据其操作的数据类型进行分类。