机器学习中的数学基础(四):概率论
- 4 概率论
- 4.1 一些概念
- 4.2 二维随机变量
- 4.2.1 离散型
- 4.2.2 连续型
- 4.3 边缘分布
- 4.3.1 离散型边缘分布
- 4.3.2 连续型边缘概率密度
- 4.4 期望
- 4.4.1 一维期望
- 4.4.2 二维期望
- 4.5 马尔可夫不等式
- 4.6 切比雪夫不等式
在看西瓜书的时候有些地方的数学推导(尤其是概率论的似然、各种分布)让我很懵逼,本科的忘光了,感觉有点懂又不太懂,基于此,干脆花一点时间简单从头归纳一下机器学习中的数学基础,也就是高数、线代、概率论(其实大学都学过)。
本文全部都是基于我自己的数学基础、尽量用方便理解的文字写的,记录的内容都是我本人记忆不太牢靠、需要时常来翻笔记复习的知识,已经完全掌握的比如极限连续性啥的都不会出现在这里。
学习内容来自这里
4 概率论
4.1 一些概念
随机事件:
是什么?扔硬币,王者峡谷击杀数,一批产品合格数。。。这些有什么特点呢?
- 可以在相同条件下重复执行
- 事先就能知道可能出现的结果
- 试验开始前并不知道这一次的结果
随机试验E的所有结果构成的集合称为E的样本空间:
S
=
{
e
}
S=\{e\}
S={e}
抛硬币:
S
=
S=
S= {正面,反面}
击杀数:
S
=
S=
S= {0,1,2,.….}
频率和概率:

实验次数越多,越稳定。
古典概型:

条件概率:
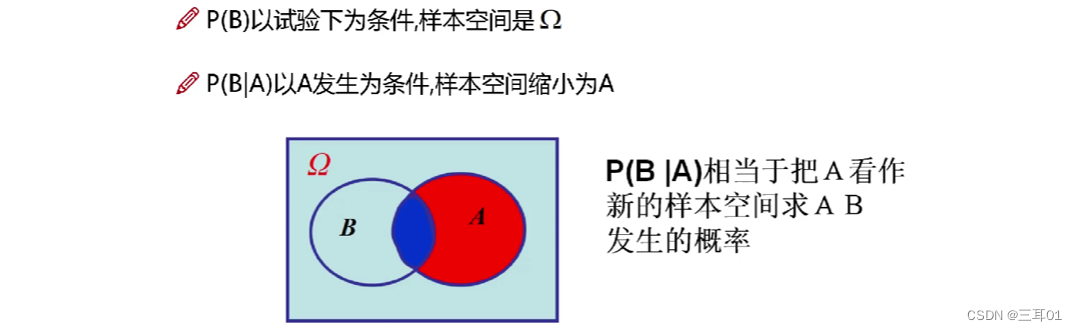

P(B|A)与P(AB):
相同点:事件A、B都发生了
不同点:样本空间不同。在P(B|A)中,事件A成为样本空间,在P(AB)中,样本空间仍为 Ω \Omega Ω。
独立性:

重复独立试验:
- 重复独立试验:在相同的条件下,将试验E重复进行,且每次试验是独立进行的,即每次试验各种结果出现的概率不受其他各次试验结果的影响。
- n重伯努利试验:若一试验的结果只有两个,A和
A
‾
\overline{A}
A,在相同的条件下,将试验独立地重复进行n次,则称这n次试验所组成的试验为n重伯努利试验或伯努利概型。
计算:

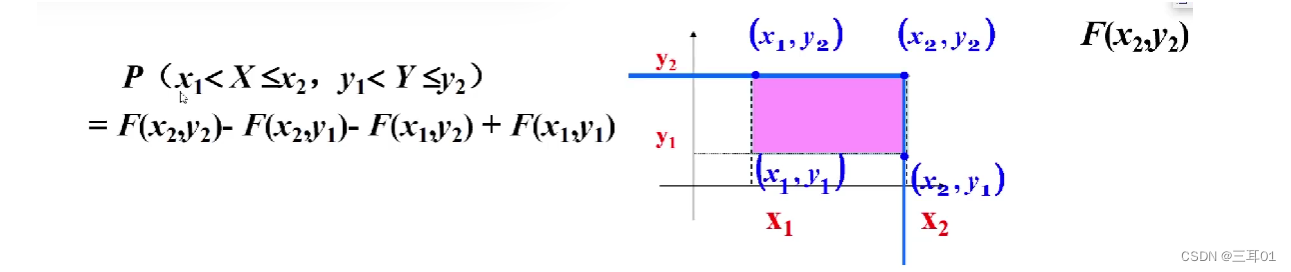
4.2 二维随机变量
有两个指标,不仅要观察两个指标各自的情况,还要了解其相互的关系。

4.2.1 离散型

4.2.2 连续型

举例子:
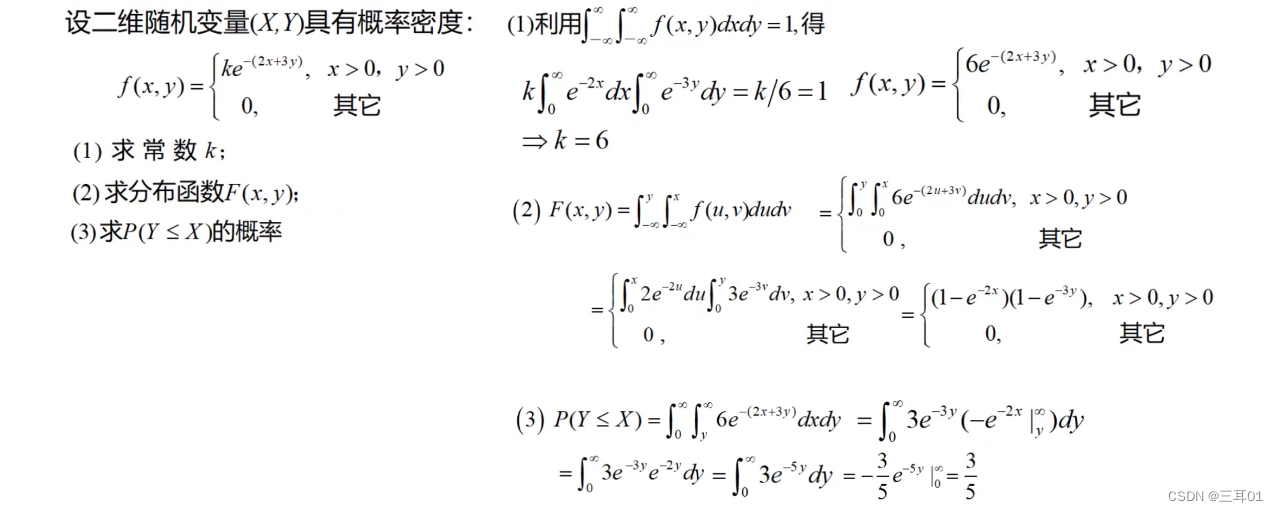
4.3 边缘分布
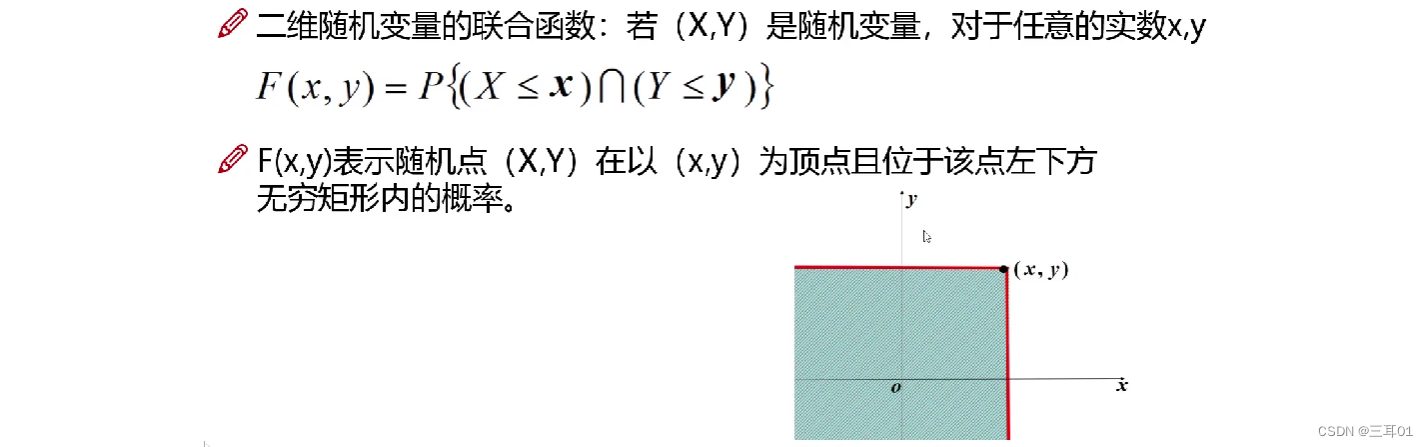
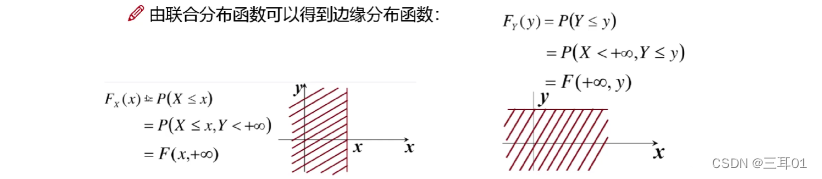
边缘分布函数:二维随机变量(X, Y)作为整体,有分布函数F(x,y)。其中,X和y都是随机变量,它们的分布函数记为:
F
X
(
x
)
F_X(x)
FX(x),
F
Y
(
y
)
F_Y(y)
FY(y),称为边缘分布函数。
在分布函数F(x,y)中令y趋向于正无穷,就能得到
F
X
(
x
)
F_X(x)
FX(x):
4.3.1 离散型边缘分布
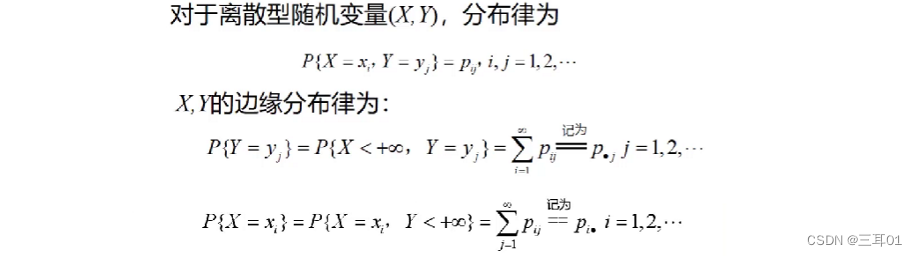
4.3.2 连续型边缘概率密度
连续型的边缘概率密度
对于连续型随机变量
(
X
,
Y
)
(X, Y)
(X,Y) ,概率密度为
f
(
x
,
y
)
f(x, y)
f(x,y)
X
,
Y
X, Y
X,Y 的边缘概率密度为:
f
X
(
x
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
y
,
f
Y
(
y
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
x
f_X(x)=\int_{-\infty}^{+\infty} f(x, y) d y,f_Y(y)=\int_{-\infty}^{+\infty} f(x, y) d x
fX(x)=∫−∞+∞f(x,y)dy,fY(y)=∫−∞+∞f(x,y)dx
事实上:
F
X
(
x
)
=
F
(
x
,
+
∞
)
=
∫
−
∞
x
[
∫
−
∞
+
∞
f
(
t
,
y
)
d
y
]
d
t
=
∫
−
∞
x
f
X
(
t
)
d
t
F_X(x)=F(x,+\infty)=\int_{-\infty}^x\left[\int_{-\infty}^{+\infty} f(t, y) d y\right] d t=\int_{-\infty}^x f_X(t) d t
FX(x)=F(x,+∞)=∫−∞x[∫−∞+∞f(t,y)dy]dt=∫−∞xfX(t)dt
同理:
F
Y
(
y
)
=
F
(
+
∞
,
y
)
=
∫
−
∞
y
[
∫
−
∞
+
∞
f
(
x
,
t
)
d
x
]
d
t
=
∫
−
∞
y
f
Y
(
t
)
d
t
F_Y(y) =F(+\infty, y)=\int_{-\infty}^y\left[\int_{-\infty}^{+\infty} f(x, t) d x\right] d t =\int_{-\infty}^y f_Y(t) d t
FY(y)=F(+∞,y)=∫−∞y[∫−∞+∞f(x,t)dx]dt=∫−∞yfY(t)dt
举例子:

4.4 期望
4.4.1 一维期望
离散型:
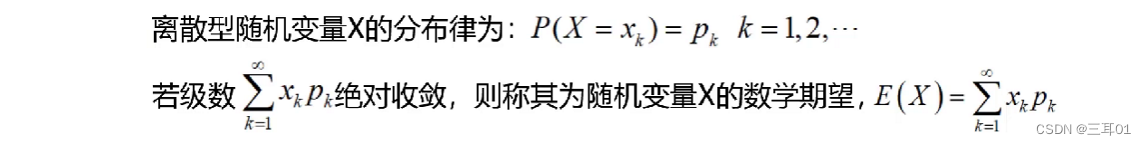
连续型:

4.4.2 二维期望

期望的性质:

4.5 马尔可夫不等式
方差:
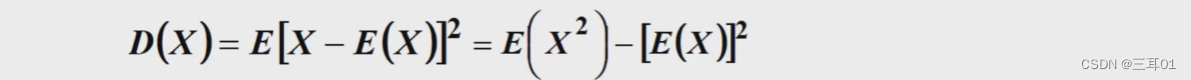
大数定理:在试验样本不变的条件下,重复试验多次,随机事件的频率近似于它的概率。
小的样本试验不足以以偏概全因为有一些局限。
马尔可夫不等式:
P
(
X
≥
a
)
≤
E
(
X
)
a
,
X
≥
0
,
a
>
0
P(X\geq a)\leq \frac{E(X)}{a},\quad X\geq 0, a>0
P(X≥a)≤aE(X),X≥0,a>0
证明:由
X
≥
0
X\geq 0
X≥0,
X
≥
a
X\geq a
X≥a 可知,
X
a
≥
1
\frac{X}{a}\geq1
aX≥1,那么:
P
(
X
≥
a
)
=
∫
a
+
∞
f
(
x
)
d
x
≤
∫
a
+
∞
X
a
d
x
P(X\geq a)=\int_{a}^{+\infty} f(x) dx\leq \int_{a}^{+\infty} \frac{X}{a} dx
P(X≥a)=∫a+∞f(x)dx≤∫a+∞aXdx。则:

4.6 切比雪夫不等式
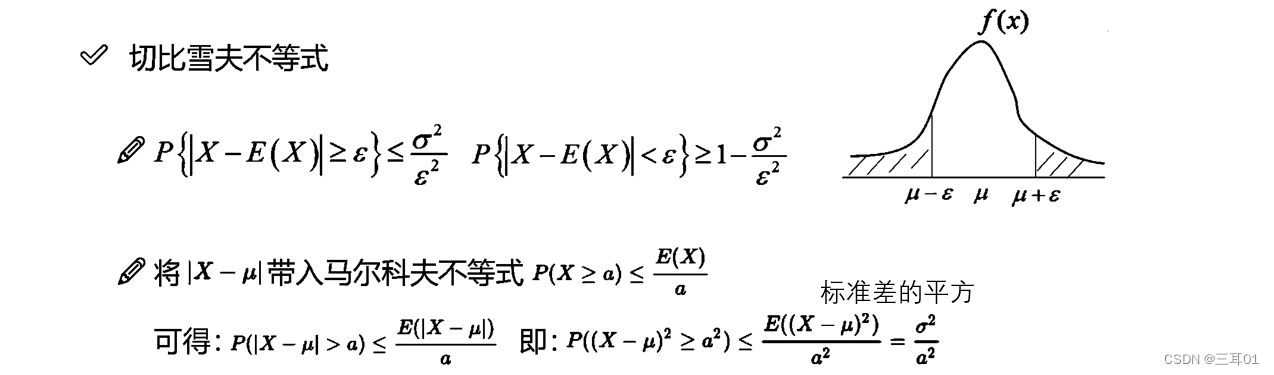
中心极限定理:样本的平均值约等于总体的平均值。不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的整体平均值周围,并且呈正态分布。