数据结构五：线性表之带头结点的双向链表的设计

news2025/1/16 15:44:41

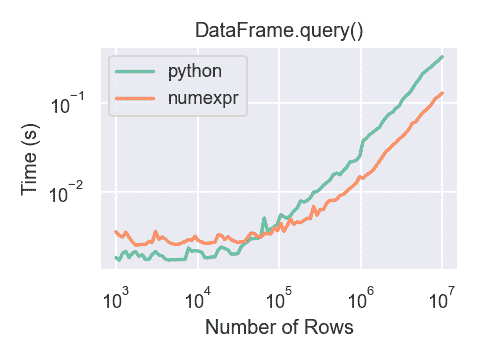
      我们在单链表中，有了next指针,这就使得我们要查找下一结点的时间复杂度为O(1)。可是如果我们要查找的是上一结点的话，那最坏的时间复杂度就是0[n)了，因为我们每次都要从头开始遍历查找。为了克服单向性这一缺点， 我们的老科学家们，设计出了双向链表。那么，它是如何解决的呢？请听我道来。

目录

一、双向链表的产生原因

二、双向链表的优势

三、双向链表的基本概念和结构

3.1 双向链表的基本概念

3.2 双向链表的结构

三、带头结点的双向链表的接口函数实现

3.1  双向链表结点设计（结构体）

3.2  双向链表的初始化

3.3 头插 

3.4 尾插

3.5 按位置插入

3.6 头删

3.7 尾删

3.8 按位置删除

3.9 按值删

3.10 查找

3.11 获取有效值个数

3.12 判空

3.13 销毁

3.14 打印

五、测试

六、总结

一、双向链表的产生原因

        前面我们学过单向链表和循环链表，在单向链表中，每个元素被称为节点（node），每个节点包含两部分：数据域和指针域。链表的第一个节点称为头节点，而最后一个节点的指针指向NULL，表示链表的末尾。由于每个节点只有一个指针指向下一个节点，因此单链表只能单向遍历。这也是它被称为“单向链表”的原因。单链表在进行头插和头删的操作时，非常的便利，时间复杂度为O(1)，但在进行任意位置的插入和删除时，必须要从头开始遍历，找到合适的位置进行插入和删除，时间复杂度为O(n)，这正是因为单向链表的缺点，只能从前向后遍历；而循环链表则不同，完全可以使用O(1)的时间来访问第一个节点和尾节点。相比单链表，循环链表解决了一个很麻烦的问题。 即可以从任意一个结点出发，而不一定是要从头结点出发，就可访问到链表的全部结点，并且访问尾巴结点的时间复杂度也可以达到O(1)。这二者有一个共同的特点就是单向的，只能从前向后遍历，不能够直接找到前驱结点。而本节讲的双向链表就是来解决这个问题的，随着链表结构的复杂化，可以实现的功能也越来越强大。

二、双向链表的优势

 双向链表作为一种数据结构，具有许多独特的优点，使其在许多场景中成为一种理想的选择。以下是对双向链表优点的详细分析：

  1. 高效地访问前驱结点和后继结点：双向链表中的每个结点都包含指向前驱结点和后继结点的指针，这使得我们可以从两个方向访问链表中的元素。这种设计使得查找、插入和删除操作更加高效。与单向链表相比，双向链表在处理这些操作时具有更好的性能。
  2. 无需查找前驱结点即可删除元素：在单向链表中，如果要删除某个结点，必须先找到其前驱结点。而在双向链表中，由于每个结点都包含指向前驱结点的指针，因此无需查找前驱结点即可删除该结点。这种特性使得双向链表的删除操作更加简便和高效。
  3. 支持从两端进行遍历：由于双向链表具有指向前驱和后继结点的指针，因此可以从链表的头部和尾部同时开始遍历。这种特性使得双向链表在进行遍历操作时具有更高的效率。
  4. 空间复杂度更低：与单向链表相比，双向链表需要更多的存储空间来存储指向前驱和后继结点的指针。但是，由于双向链表在处理操作时具有更高的效率，因此在实际应用中，双向链表的空间复杂度更低。

三、双向链表的基本概念和结构

3.1 双向链表的基本概念

     双向链表(double linked list) 是在单链表的每个结点中，再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域，一个指向直接后继，另一个指向直接前驱。

3.2 双向链表的结构

      下图为存在有效结点时的带头结点的双向链表，每个结点有两个指针域，一个保存后继结点的地址，一个保存前驱结点的地址。

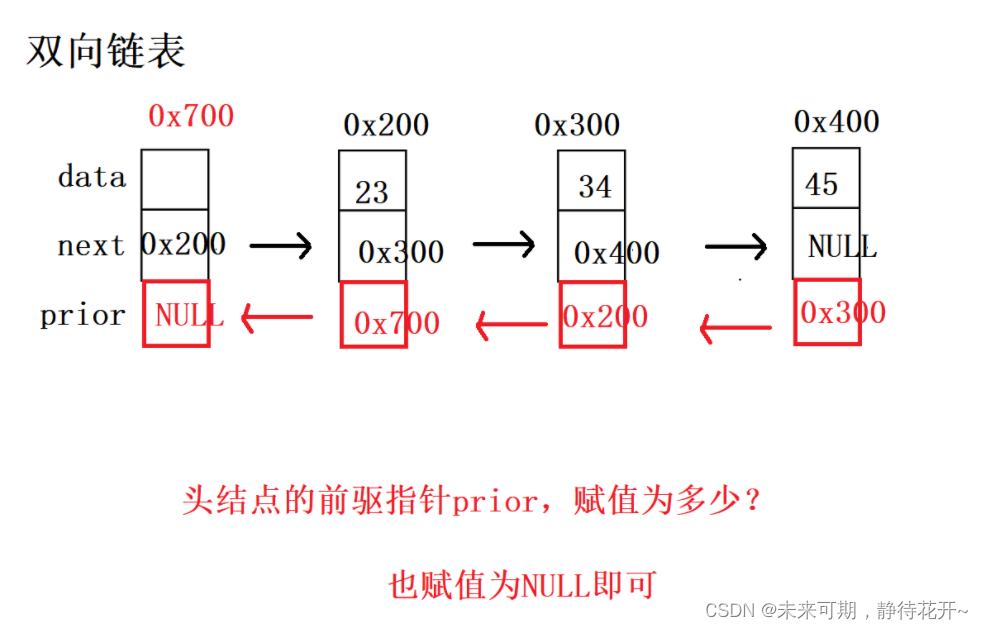
      下图为不存在有效结点时的带头结点的双向链表（空链表），每个结点有两个指针域，并且同时指向空NULL。

三、带头结点的双向链表的接口函数实现

 双向链表的基本操作也同样有：初始化，头插，尾插，按位置插，头删，尾删，按位置删，查找，按值删，获取有效值个数，判空，清空，销毁，打印。这里详细展示这些基本操作的实现思想和画图分析以及代码实现和算法效率分析，

      注意：同样双向链表与顺序表不同，由于它是按需索取，因此，不需要进行判满和扩容操作；

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include "double_list.h"

//初始化
void Init_Dlist(struct DNode *dls);

//头插
void Insert_head(PDNode dls, ELEM_TYPE val);


//尾插
void Insert_tail(PDNode dls, ELEM_TYPE val);

//按位置插
void Insert_pos(PDNode dls, ELEM_TYPE val, int pos);

//头删
void Del_head(PDNode dls);

//尾删
void Del_tail(PDNode dls);

//按位置删
void Del_pos(PDNode dls, int pos);

//按值删
void Del_val(PDNode dls, ELEM_TYPE val);

//搜索
struct DNode *Search(PDNode dls, ELEM_TYPE val);

//判空
bool Empty(PDNode dls);

//获取有效长度
int Get_length(PDNode dls);

//打印
void Show(PDNode dls);

//销毁
void Destroy1(PDNode dls);

void Destroy2(PDNode dls);

//清空 (顺序表的清空和销毁不一样， 但是单链表的两个函数一回事)

3.1  双向链表结点设计（结构体）

      双向链表结构体设计也很简单，和单链表节点结构体设计相比,多了一个指向前驱结点的指针域，每个结点包括三个部分：存储数据的数据域和两个指针域，一个保存后继结点的地址，一个保存前驱结点的地址。因此设计结点主要设计这三个成员变量。

       强调结构体自身引用（自己嵌套自己必须使用struct，即使使用typedef关键字进行重命名）结构体内部不可以定义自身的结构体变量，但是可以定义自身结构体指针变量，因为指针与类型无关，占用内存空间就是4个字节！

typedef int ELEM_TYPE;


//双向链表有效结点设计
typedef struct DNode
{
	ELEM_TYPE data;//数据域
	struct DNode* next;//直接后继指针
	struct DNode* prior;//直接前驱指针
}Node, *PDNode;


//双向链表头结点设计
//因为双链表的头结点可以借用有效结点的结构体设计，只不过将数据域浪费掉，只使用其两个指针域

3.2  双向链表的初始化

     双向链表的初始化主要是对其指针域赋值，数据域不使用，不需要操作！并且初始化并没有有效节点，因此，两个指针域应该都赋NULL。

//初始化
void Init_Dlist(struct DNode *dls)
{
	第0步：传入的指针检测
    assert(dls!=NULL);
   
    //数据域不用处理
	dls->next = dls->prior = NULL;   //对前驱指针和后继指针赋值为NULL
}

3.3 头插 

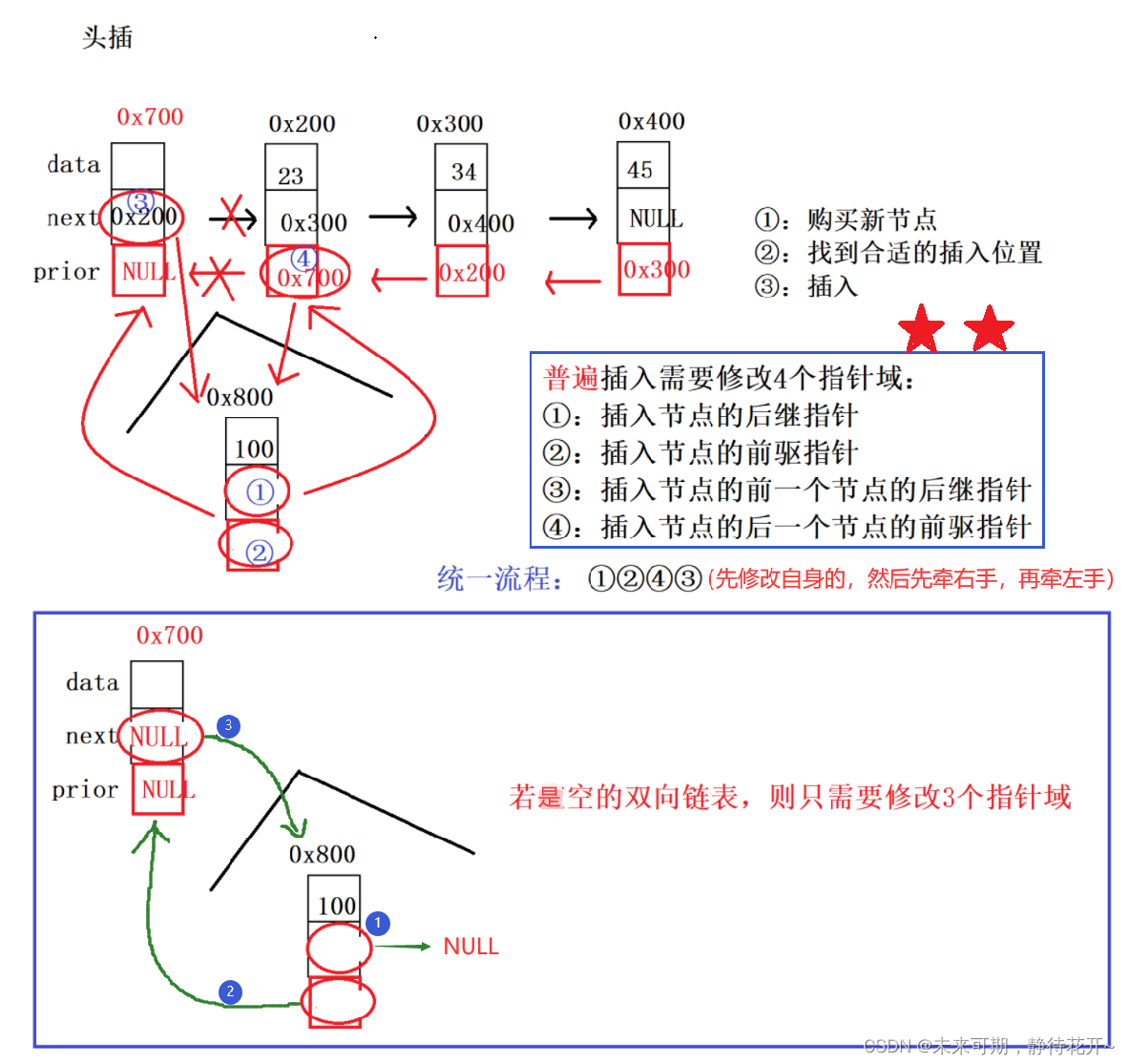
双向链表和单链表的头插法的思想是一样的，只不过需要多修改两个指针域。

头插的基本思路如下：

    第0步：assert对传入的指针检测；

    第1步：购买新节点（购买好节点之后，记得将val值赋值进去）；

    第2步：找到合适的插入位置；

    第3步：插入，要修改四个指针域，注意通用的核心代码（四个步骤），先牵右手，再牵左手！！！否则会发生内存泄漏。

     注意：当链表为空时(链表没有有效节点)，此时便只需要修改三个指针域，因此在头插操作时，进行判空操作，分两种情况执行：要么修改四个指针域，要么只需要修改三个指针域！！！

//头插
void Insert_head(PDNode dls, ELEM_TYPE val)
{
	//0.传入的指针检测
    assert(dls!=NULL);

	//1.购买新节点
	PDNode pnewnode = (PDNode)malloc(1*sizeof(struct DNode));
	pnewnode->data = val;

	//2.找到合适的插入位置(头插，不用管，直接用dls即可)

	//3.通过判断双向链表是否是空链表，来决定到底修改3个还是4个指针域

	pnewnode->next = dls->next;//①
	pnewnode->prior = dls;//②

	if(!Empty(dls))//④
	{
		pnewnode->next->prior = pnewnode;
	}
	dls->next = pnewnode;//③
}

 

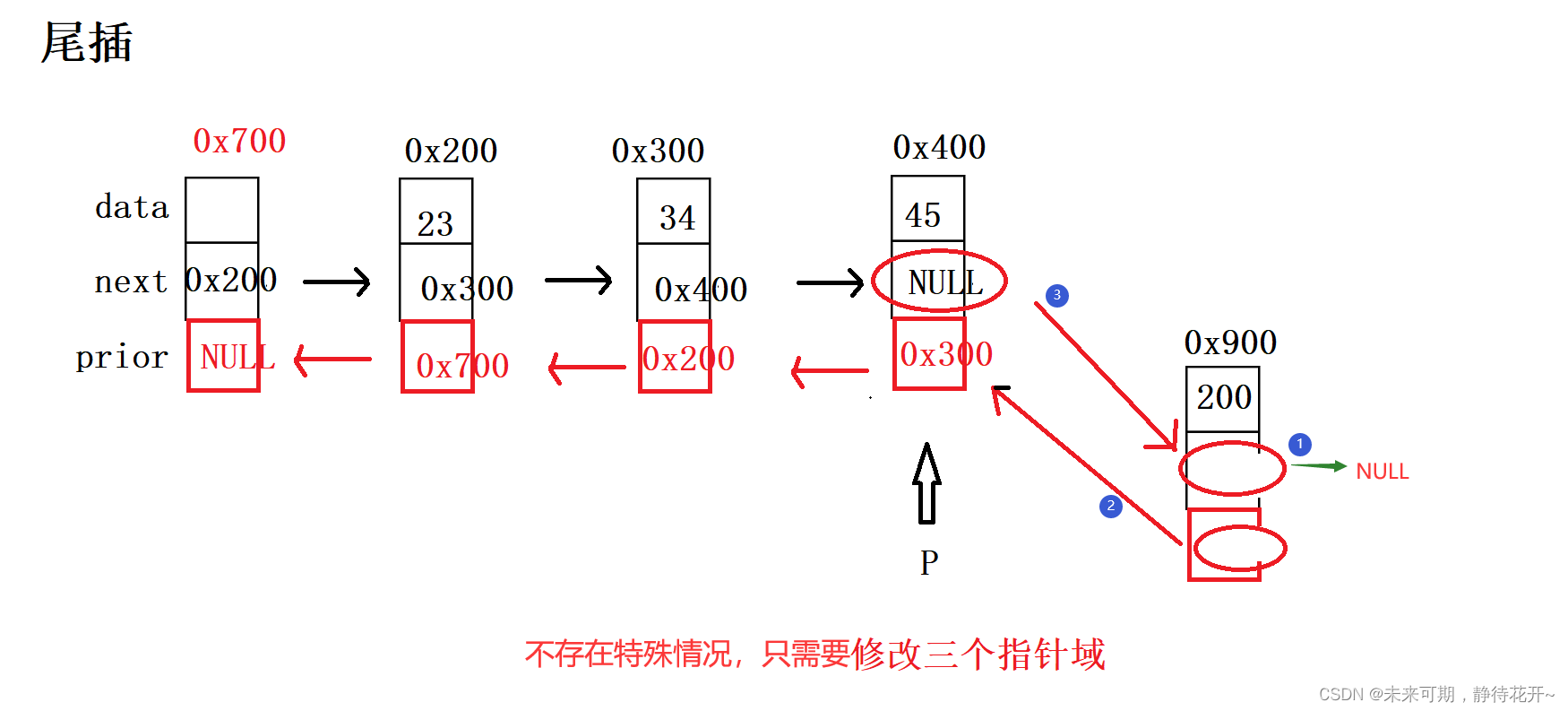
3.4 尾插

尾插的基本思路如下：

    第0步：assert对传入的指针检测；

    第1步：购买新节点（购买好节点之后，记得将val值赋值进去）；

    第2步：找到合适的插入位置，在这里就是找到最后一个有效结点，如何找？因为最后一个有效结点的指针域为NULL，只需要从头开始通过地址，遍历每一个结点，直到遇到最后一个节点，此时指针域指向NULL；

    第3步：利用插入的通用思路，只不过这里只需要修改三个指针域，并且没有特殊情况。

//尾插
void Insert_tail(PDNode dls, ELEM_TYPE val)
{
	//0.传入的指针检测
    assert(dls!=NULL);

	//1.购买新节点
	struct DNode* pnewnode = (struct DNode* )malloc(sizeof(struct DNode));
	pnewnode->data = val;

	//2.找到合适的插入位置，用p指针指向
	struct DNode *p = dls;
	for(; p->next!=NULL; p=p->next);


	//3.尾插不存在特殊情况，统一修改3个指针域
	pnewnode->next = p->next;
	pnewnode->prior = p;

	p->next = pnewnode;//pnewnode->prior->next = pnewnode;
}

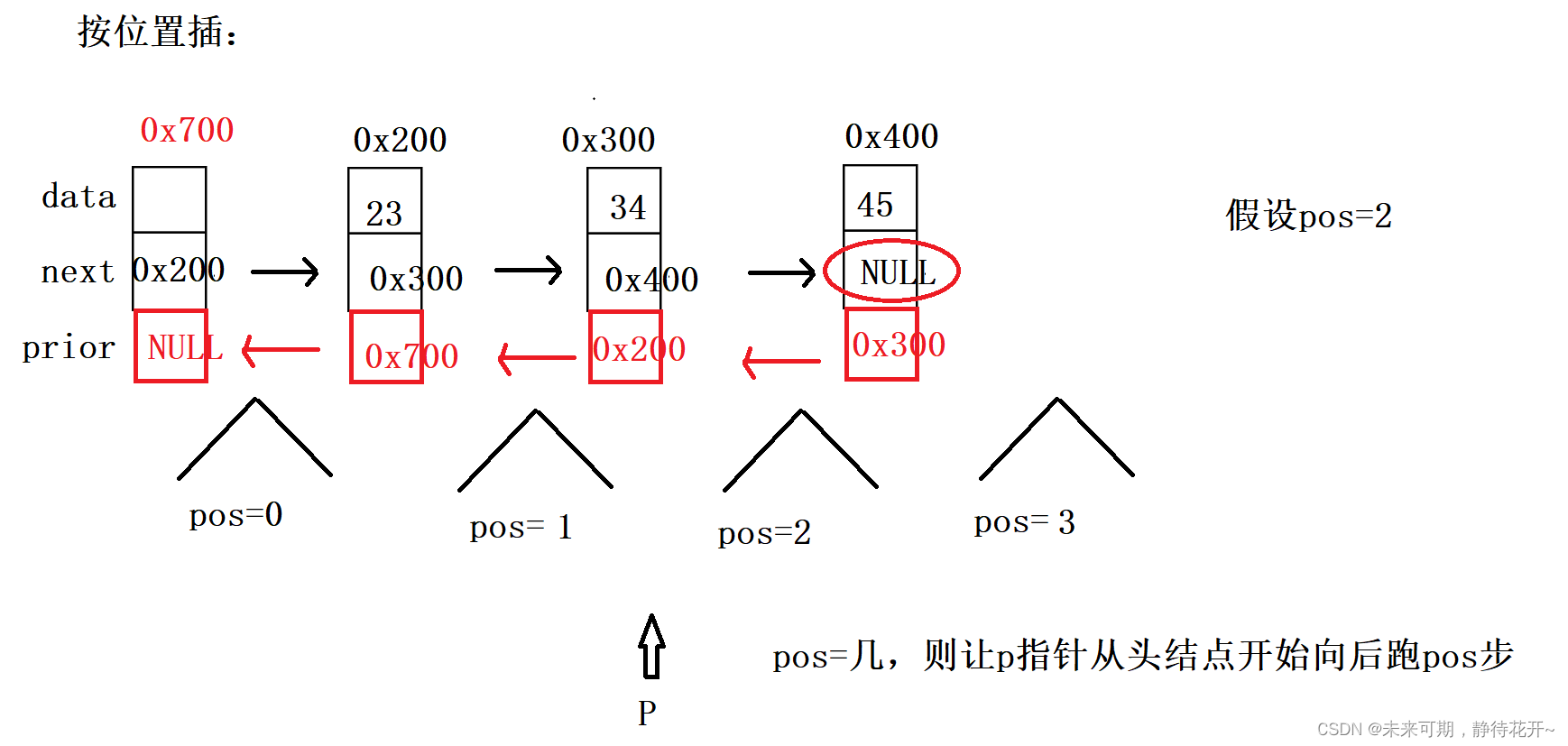
3.5 按位置插入

按位置插入的基本思路如下：

    第0步：assert对传入的指针和插入的位置检测；要插入的位置必须大于等于零且小于等于  链表总长度。

    第1步：购买新节点（购买好节点之后，记得将val值赋值进去）；

    第2步：找到合适的插入位置，在这里就是找到插入位置的前一个结点，如何找？用指针p指向(例如pos=2，则让临时指针p，从头结点开始向后走pos步)

    第3步：利用插入的通用思路；

注意：按位置插入，如果pos=0，此时为头插存在特殊情况，需要判断链表是否为空，如果pos为有效结点个数，此时为尾插，只需要修改3个指针域，其他情况就是正常的插入，修改4个指针域。

//按位置插
void Insert_pos(PDNode dls, ELEM_TYPE val, int pos)
{
	//0.传入的指针检测
    assert(dls!=NULL);

	//0.5 对pos做合法性判断 并且pos=0的时候，只需要修改3个指针域

	assert(pos>=0 && pos<=Get_length(dls));

    //此时为头插
	if(pos == 0)
	{
		Insert_head(dls, val);
		return;
	}

	//1.购买新节点
	struct DNode* pnewnode = (struct DNode* )malloc(sizeof(struct DNode));
	pnewnode->data = val;

	//2.找到合适的插入位置，用p指针指向
	struct DNode *p = dls;
	for(int i=0; i<pos; i++)
	{
		p=p->next;
	}
	
	//3.按位置插入，若pos=0为特殊情况，在前面通过if判断的形式已经处理过了，则现在都为普遍情况
	pnewnode->next = p->next;
	pnewnode->prior = p;

	if(pnewnode->next != NULL)//若待插入节点的下一个节点存在,即它不是尾插
	{
		pnewnode->next->prior = pnewnode;//则让下一个节点的前驱指向pnewnode
	}

	p->next = pnewnode;
}

3.6 头删

    对于删除操作，则需要对链表进行判空操作！并且删除操作遵循基本同样的4个步骤，需要理解加记忆。删除操作的基本思路如下：

①:用指针q指向待删除节点；
②:用指针p指向待删除节点的前驱节点,双向链表就很方便，不需要从头开始遍历；(头删的话，这里p可以被dls代替)
③:跨越指向，修改两个指针域
④:释放待删除节点。

注意：头删存在特殊情况，若双向链表只有一个有效节点，只需要修改一个指针域的指向！

 

//头删
void Del_head(PDNode dls)
{
	//0.传入的指针检测
    assert(dls!=NULL);

	//1.判空
	if(Empty(dls))
	{
		return;
	}

	if(dls->next->next == NULL)//特殊情况：有且仅有一个有效节点
	{
		free(dls->next);
		dls->next = NULL;
		return;
	}

	//2.找到待删除节点用q指向，再找到待删除结点的上一个节点，用p指向待删除节点的上一个节点
	struct DNode *q = dls->next;
	//p可以不用申请，因为头删的话 p就是dls

	//3.跨越指向+释放
	dls->next = q->next;
	q->next->prior = dls;
	free(q);
	q = NULL;
	
}

3.7 尾删

       尾删的基本思路还是那四个步骤，只是具体实现的方式不一样。

//尾删
void Del_tail(PDNode dls)
{
	//0.传入的指针检测
    assert(dls!=NULL);

	//1.判空
	if(Empty(dls))
	{
		return;
	}

	//2.找到待删除节点用q指向，再找到待删除结点的上一个节点，用p指向待删除节点的上一个节点
	struct DNode *q = dls;
	for(; q->next!=NULL; q=q->next);

	/*struct DNode *p = dls;
	for(; p->next!=q; p=p->next);*/ //老方法

	struct DNode *p = q->prior;     //直接找到前驱节点，不用从头遍历

	//3.跨越指向+释放
	p->next = q->next;
	free(q);
	q = NULL;
}

3.8 按位置删除

      根据位置删除结点，需要判断结点的合法性，这次的pos需要小于链表长度，基本思路还是那四个步骤，只是具体实现的方式不一样。

//按位置删
void Del_pos(PDNode dls, int pos)
{
	//0.传入的指针检测
    assert(dls!=NULL);

	//0.5 pos做合法性判断  pos=0这种特殊情况要提前处理
	assert(pos>=0 && pos<=Get_length(dls)-1);

	//1.pos=几，指针q从头结点开始向后跑pos+1步， 指针p从头结点开始向后跑pos步
	struct DNode *q = dls;
	for(int i=0; i<pos+1; i++)
	{
		q = q->next;
	}

	/*struct DNode *p = dls;
	for(int j=0; j<pos; j++)
	{
		p = p->next;
	}*/     //老方法

	struct DNode *p = q->prior;   //直接找到前驱，不需要从前向后遍历
	
	//2.跨越指向+释放
	p->next = q->next;
	free(q);
	q = NULL;

}

3.9 按值删

     按值删需要先找到数据域是该值的结点，然后将其删除，基本思路还是那四个步骤，只是具体实现的方式不一样。

注意：存在特殊情况，只有一个有效结点，返回的结点就是这个有效结点，就是头删的特殊情况，只需要修改一个指针域！

//按值删
void Del_val(PDNode dls, ELEM_TYPE val)
{
    //0.传入的指针检测
    assert(dls!=NULL);

	struct DNode *p = Search(dls, val);
	//未找到，不存在该节点
	if(p == NULL)
	{
		return;
	}

	//特殊情况处理：只有一个有效结点，返回的结点就是这个有效结点，就是头删的特殊情况，只需要修改一个指针域
	if(p->next == NULL && p->prior == dls)
	{
		free(p);
		dls->next = NULL;
		return;
	}

	/*struct DNode *q = dls;
	for( ; q->next!=p; q=q->next);*/  //老方法，直接从前向后遍历

	struct DNode *q = p->prior;      //直接找到该节点的前驱结点


	//跨越指向+释放
	q->next = p->next;
	free(p);
	p = NULL;
}

3.10 查找

 按值查找，返回该值的结点，查找操作只需要定义一个临时结点类型指针变量，让它从第一个有效节点开始遍历，只要结点存在就往后遍历。


//搜索
struct DNode *Search(PDNode dls, ELEM_TYPE val)
{
    //0.传入的指针检测
    assert(dls!=NULL);

    struct DNode *p = dls->next;
	for(; p!=NULL; p=p->next)
	{
		if(p->data == val)
		{
			return p;
		}
	}

	return NULL;
}

3.11 获取有效值个数

    只需要定义一个临时结点类型指针变量，让它从第一个有效节点开始遍历，只要没有到最后一个结点就往后遍历。 采用计数器思想，计数器加1，返回计数器变量即是有效结点个数。

//获取有效长度
int Get_length(PDNode dls)
{
    //0.传入的指针检测
    assert(dls!=NULL);

	struct DNode *p = dls->next;
	int count = 0;

	for(; p!=NULL; p=p->next)
	{
		count++;
	}

	return count;
}

3.12 判空

     在进行删除操作时，需要对链表进行判空操作，如果链表为空，则无法删除！！如何判断链表为空？在链表只有一个头结点时，代表链表为空，此时就是最初始的状态，只有一个头结点，并且头结点的指针域为NULL，因此，只需要判断头结点的指针域是否为NULL，便可以知道链表是否为空。

//判空
bool Empty(PDNode dls)
{
    //0.传入的指针检测
    assert(dls!=NULL);

	return dls->next == NULL;
}

3.13 销毁

第一种：无限头删

       只要链表不为空，一直调用头删函数，直到把所有结点删除完，此时，退出循环。

第二种：不借助头结点，但是需要两个指针变量p和q(双指针思想)。

//销毁
void Destroy1(PDNode dls);

void Destroy2(PDNode dls)
{
   //0.传入的指针检测
    assert(dls!=NULL);

	struct DNode *q = dls->next;
	struct DNode *p = NULL;

	dls->next = NULL;

	while(q!=NULL)
	{
		p = q->next;
		free(q);
		q = p;
	}

}

3.14 打印

只需要定义一个临时结点类型指针变量，让它从第一个有效节点开始遍历，只要没有到最后一个结点就往后遍历，同时打印结构体的数据域成员。

//打印
void Show(PDNode dls)
{
    //0.传入的指针检测
    assert(dls!=NULL);
	struct DNode *p = dls->next;

	for(; p!=NULL; p=p->next)
	{
		printf("%d ", p->data);
	}

	printf("\n");
}

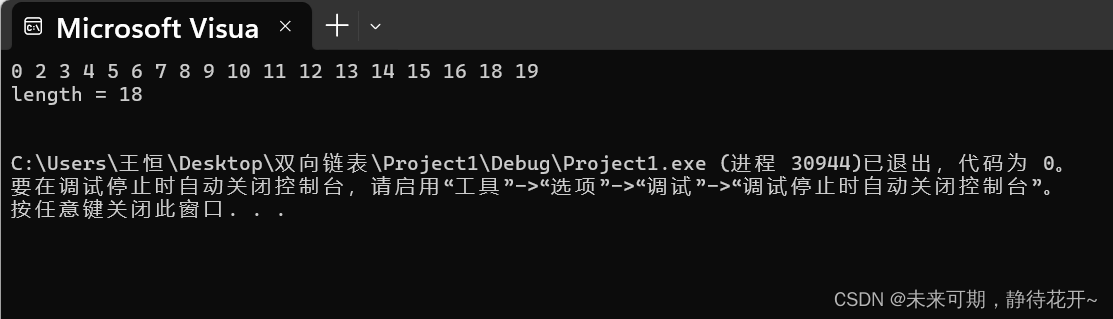
五、测试

int main()
{

	struct DNode head;
	Init_Dlist(&head);
	
	for(int i=0; i<20; i++)
	{
		Insert_pos(&head, i, i);
	}
	
	Insert_head(&head, 100);
	Insert_tail(&head, 200);

	Del_head(&head);
	Del_tail(&head);

	Del_pos(&head, 1);
	Del_val(&head, 17);

	Show(&head);

	int len = Get_length(&head);
	printf("length = %d\n", len);

	Destroy2(&head);
	Show(&head);

}

六、总结

      在单向链表中，如果要删除某个结点，必须先找到其前驱结点。而在双向链表中，由于每个结点都包含指向前驱结点的指针，因此无需查找前驱结点即可删除该结点。这种特性使得双向链表的删除操作更加简便和高效。因此，一个操作涉及到找一个结点的前驱结点时，双向链表是非常方便的，只需要访问它的前驱指针！！！

      双向链表有很多地方存在特殊情况，需要单独处理，因此，我们需要不断巩固，加深对于双向链表的理解，才能够灵活运用！

     以上便是我为大家带来的带头结点的双向链表设计内容，若有不足，望各位大佬在评论区指出，谢谢大家！可以留下你们点赞、收藏和关注，这是对我极大的鼓励，我也会更加努力创作更优质的作品。再次感谢大家！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1628448.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

springcloud按版本发布微服务达到不停机更新的效果

springcloud按版本发布微服务达到不停机更新的效果

本文基于以下环境完成 spring-boot 2.3.2.RELEASEspring-cloud Hoxton.SR9spring-cloud-alibaba 2.2.6.RELEASEspring-cloud-starter-gateway 2.2.6.RELEASEspring-cloud-starter-loadbalancer 2.2.6.RELEASEnacos 2.0.3 一、思路 实现思路&#xff1a; 前端项目在请求后端接…
阅读更多...
【优质书籍推荐】AIGC时代的PyTorch 深度学习与企业级项目实战

【优质书籍推荐】AIGC时代的PyTorch 深度学习与企业级项目实战

大家好&#xff0c;我是herosunly。985院校硕士毕业&#xff0c;现担任算法研究员一职&#xff0c;热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名&#xff0c;CCF比赛第二名&#xff0c;科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的…
阅读更多...
Facebook的未知力量：数字世界的新引擎

Facebook的未知力量：数字世界的新引擎

在数字化的时代&#xff0c;社交媒体已经成为了我们日常生活中不可或缺的一部分&#xff0c;而Facebook作为其中的巨头&#xff0c;其影响力远远超出了我们的想象。但是&#xff0c;Facebook背后隐藏的力量和影响远不止于此&#xff0c;它正逐渐成为数字世界的新引擎&#xff0…
阅读更多...
设计模式：单例、原型和生成器

设计模式：单例、原型和生成器

在这篇文章中&#xff0c;我们将重点介绍其余的创建模式&#xff1a;Singleton&#xff0c;Builder和Prototype。 在我看来&#xff0c;这些模式不如工厂重要。然而&#xff0c;了解它们仍然很有用。我将提供UML描述&#xff0c;简单的java示例&#xff08;这样即使你不了解jav…
阅读更多...
stm32 hid自定义接收发送程序开发过程记录

stm32 hid自定义接收发送程序开发过程记录

cubleMX配置如下 修改端点描述符一次传输的数据大小 根据cubelMX标准在这里修改 编译错误 直接修改&#xff08;因为没有使用nodef &#xff09;编译通过 修改报告描述符&#xff08;默认的描述符无法传输数据&#xff09; 参考&#xff1a;USB协议详解第10讲&#xff08;USB描…
阅读更多...
基于SpringBoot的“在线BLOG网”的设计与实现（源码+数据库+文档+PPT)

基于SpringBoot的“在线BLOG网”的设计与实现（源码+数据库+文档+PPT)

基于SpringBoot的“在线BLOG网”的设计与实现&#xff08;源码数据库文档PPT) 开发语言&#xff1a;Java 数据库&#xff1a;MySQL 技术&#xff1a;SpringBoot 工具&#xff1a;IDEA/Ecilpse、Navicat、Maven 系统展示 在线BLOG网结构功能图 管理员登录功能界面 用户信息…
阅读更多...
电脑屏幕监控软件有哪些？大型企业都在用的电脑屏幕监控软件

电脑屏幕监控软件有哪些？大型企业都在用的电脑屏幕监控软件

电脑监控软件&#xff0c;这个东西真的很重要&#xff0c;就像保镖一样&#xff0c;保护我们的电脑和数据安全。它能预防坏事发生&#xff0c;还能在事情发生时及时控制&#xff0c;事后还能帮我们找出问题的根源。对于那些经常担心数据泄密的企业来说&#xff0c;电脑屏幕监控…
阅读更多...
2024 XYCTF Web 方向 wp 全解

2024 XYCTF Web 方向 wp 全解

2024 XYCTF Web 方向 全解 文章目录 2024 XYCTF Web 方向 全解Webezhttp考点:信息泄露基础发包 warm up考点:php黑魔法变量覆盖 ezRCE考点:无字母RCE(bashfuck)shell变量构造RCE ezmd5考点:md5文件强相等 ezunserilze考点&#xff1a;引用绕过强相等php原生类读文件 牢牢记住&a…
阅读更多...
【加密周报】中美下周有“大事”发生！准备联手引爆比特币大行情？美国大型养老基金和梅隆银行已持有比特币ETF！

【加密周报】中美下周有“大事”发生！准备联手引爆比特币大行情？美国大型养老基金和梅隆银行已持有比特币ETF！

自减半之后&#xff0c;比特币便进入了横盘状态&#xff0c;始终在6-6.5万美元价格区间震荡。4月24日&#xff0c;香港证监会官网正式公示虚拟资产现货ETF获批名单&#xff0c;华夏&#xff08;香港&#xff09;、嘉实国际、博时国际旗下相关产品均在其列&#xff0c;并计划将于…
阅读更多...
打印给定数组中每一个数字

打印给定数组中每一个数字

如何给定1-10的数字 #include<stdio.h> int main() {int arr[] { 1,2,3,4,5,6,7,8,9,10 };// 0 9//[]--下标引用操作符int i;int sz sizeof(arr) / sizeof(arr[0]);//10个数for (i 0; i < sz; i){printf("%d ", arr[i]);}re…
阅读更多...
【项目分享】用 Python 写一个桌面倒计日程序！

【项目分享】用 Python 写一个桌面倒计日程序！

事情是这样的&#xff0c;我们班主任想委托我做一个程序&#xff0c;能显示还有几天考试。我立即理解了这个意思&#xff0c;接下了这个项目。 话不多说&#xff0c;来看看这个项目吧—— 项目简介 仓库地址&#xff1a;https://gitee.com/yaoqx/desktop-countdown-day 这是 …
阅读更多...
排序 “肆” 之归并排序

排序 “肆” 之归并排序

1. 归并排序 1.1 原理介绍 归并排序的基本原理是将一个未排序的数组分解为较小的子数组&#xff0c;然后递归地对这些子数组进行排序&#xff0c;最后再将排好序的子数组合并成一个有序数组。其核心操作是将一维数组中前后相邻的两个有序序列归并为一个有序序列。 其主要步骤包…
阅读更多...
C++链表操作入门

C++链表操作入门

数据结构基础&#xff1a;链表操作入门 数据结构基础&#xff1a;链表操作入门链表的基本概念链表的基本操作输出链表插入节点删除节点查找值 完整的链表操作示例结语 数据结构基础&#xff1a;链表操作入门 在计算机科学中&#xff0c;数据结构是组织和存储数据的方式&#x…
阅读更多...
监控上网行为的软件 五款上网行为监控软件推荐

监控上网行为的软件 五款上网行为监控软件推荐

在这个数字化时代&#xff0c;员工上网行为的管理与监控变得越来越重要。市面上涌现出众多监控员工上网的软件&#xff0c;它们各具特色&#xff0c;各有千秋。接下来&#xff0c;就让我们一起探索一下这些神奇的软件吧&#xff01; 1、安企神点击领取免费试用版 这是一款功能…
阅读更多...
LMDeploy量化部署LLMVLM实践-笔记五

LMDeploy量化部署LLMVLM实践-笔记五

本次课程由西北工业大学博士生、书生浦源挑战赛冠军队伍队长、第一期书生浦语大模型实战营优秀学员【安泓郡】讲解【OpenCompass 大模型评测实战】课程 课程视频&#xff1a;https://www.bilibili.com/video/BV1tr421x75B/ 课程文档&#xff1a;https://github.com/InternLM/…
阅读更多...
12 内核开发-任务调度之tasklet

12 内核开发-任务调度之tasklet

12 内核开发-任务调度之tasklet 课程简介&#xff1a; Linux内核开发入门是一门旨在帮助学习者从最基本的知识开始学习Linux内核开发的入门课程。该课程旨在为对Linux内核开发感兴趣的初学者提供一个扎实的基础&#xff0c;让他们能够理解和参与到Linux内核的开发过程中。 课…
阅读更多...
C++系列-命名空间

C++系列-命名空间

&#x1f308;个人主页&#xff1a;羽晨同学 &#x1f4ab;个人格言:“成为自己未来的主人~” 命名空间 在C/C中&#xff0c;变量&#xff0c;函数和后面要学到的类都是大量存在的&#xff0c;这些变量&#xff0c;函数和类的名称都存在于全局作用域中&#xff0c;可能会导…
阅读更多...
【Linux系统化学习】生产者消费者模型（阻塞队列和环形队列）

【Linux系统化学习】生产者消费者模型（阻塞队列和环形队列）

目录 生产者消费者模型 什么是生产者消费者模型 为什么要使用生产者消费者模型 生产者消费者模型的优点 为什么生产者和生产者要互斥&#xff1f; 为什么消费者和消费者要互斥&#xff1f; 为什么生产者和消费者既是互斥又是同步&#xff1f; 基于BlockingQueue的生产者…
阅读更多...
第四百八十一回

第四百八十一回

文章目录 1. 概念介绍2. 使用方法2.1 固定样式2.2 自定义样式 3. 示例代码4. 内容总结 我们在上一章回中介绍了"GetMaterialApp组件"相关的内容&#xff0c;本章回中将介绍使用get显示SnackBar.闲话休提&#xff0c;让我们一起Talk Flutter吧。 1. 概念介绍 我们在介…
阅读更多...
Pandas 2.2 中文官方教程和指南（十一·一）

Pandas 2.2 中文官方教程和指南（十一·一）

原文&#xff1a;pandas.pydata.org/docs/ PyArrow 功能 原文&#xff1a;pandas.pydata.org/docs/user_guide/pyarrow.html pandas 可以利用PyArrow来扩展功能并改善各种 API 的性能。这包括&#xff1a; 与 NumPy 相比&#xff0c;拥有更广泛的数据类型 对所有数据类型支持缺…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023