这里写目录标题
- 1 理论
- 1.1 BFS框架
- 2 例题
- 2.1 二叉树的最小高度
- 2.2 打开转盘锁
- 2.3 滑动谜题
1 理论
BFS和DFS是两个遍历算法,其中DFS之前已经接触过,就是回溯,忘记的话请回顾回溯篇的例题(全排列,N皇后)
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度可能比 DFS 大很多,至于为什么,我们后面介绍了框架就很容易看出来了。
1.1 BFS框架
我们先举例一下 BFS 出现的常见场景好吧,问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿。
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj()) {
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
}
}
// 如果走到这里,说明在图中没有找到目标节点
}
2 例题
2.1 二叉树的最小高度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例1:
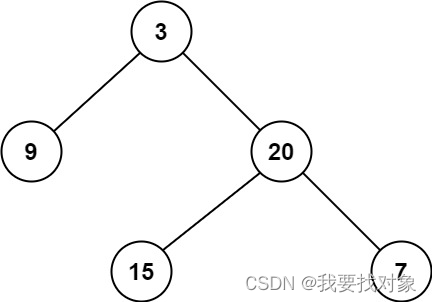
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
思路以及代码:
class Solution {
public int minDepth(TreeNode root) {
return bfs(root);
}
public int bfs(TreeNode root){
if(root == null){
return 0;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
int depth = 1;
while(!q.isEmpty()){
int sz = q.size();
for(int i = 0;i<sz;i++){
TreeNode cur = q.poll();
if(cur.left == null && cur.right == null){
return depth;
}
if(cur.left != null){
q.offer(cur.left);
}
if(cur.right != null){
q.offer(cur.right);
}
}
depth++;
}
return depth;
}
}
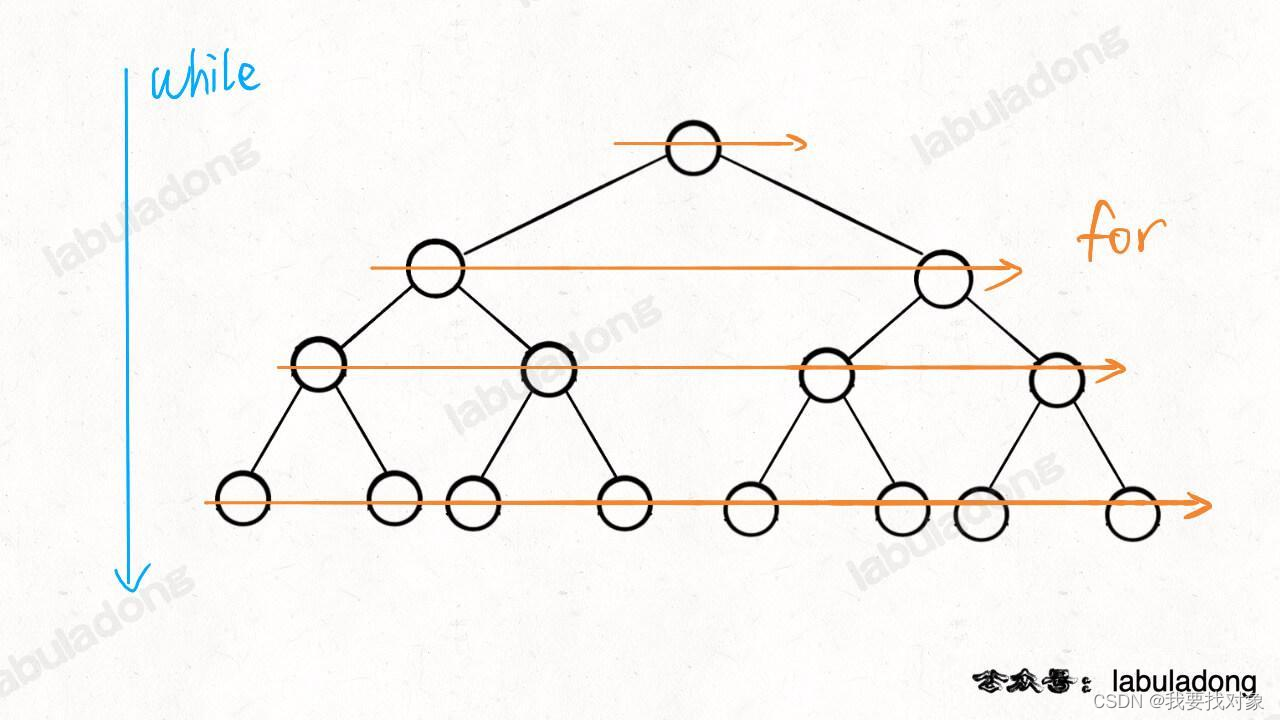
这里注意这个 while 循环和 for 循环的配合,while 循环控制一层一层往下走,for 循环利用 sz 变量控制从左到右遍历每一层二叉树节点:
2.2 打开转盘锁
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由旋转:例如把 ‘9’ 变为 ‘0’,‘0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 ‘0000’ ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
示例 1:
输入:deadends = [“0201”,“0101”,“0102”,“1212”,“2002”], target = “0202”
输出:6
解释:
可能的移动序列为 “0000” -> “1000” -> “1100” -> “1200” -> “1201” -> “1202” -> “0202”。
注意 “0000” -> “0001” -> “0002” -> “0102” -> “0202” 这样的序列是不能解锁的,
因为当拨动到 “0102” 时这个锁就会被锁定。
示例 2:
输入: deadends = [“8888”], target = “0009”
输出:1
解释:把最后一位反向旋转一次即可 “0000” -> “0009”。
示例 3:
输入: deadends = [“8887”,“8889”,“8878”,“8898”,“8788”,“8988”,“7888”,“9888”], target = “8888”
输出:-1
解释:无法旋转到目标数字且不被锁定。
思路以及代码:
第一步,我们不管所有的限制条件,不管 deadends 和 target 的限制,就思考一个问题:如果让你设计一个算法,穷举所有可能的密码组合,你怎么做?
穷举呗,再简单一点,如果你只转一下锁,有几种可能?总共有 4 个位置,每个位置可以向上转,也可以向下转,也就是有 8 种可能对吧。
比如说从 “0000” 开始,转一次,可以穷举出 “1000”, “9000”, “0100”, “0900”… 共 8 种密码。然后,再以这 8 种密码作为基础,对每个密码再转一下,穷举出所有可能…
仔细想想,这就可以抽象成一幅图,每个节点有 8 个相邻的节点,又让你求最短距离,这不就是典型的 BFS 嘛,框架就可以派上用场了,先写出一个「简陋」的 BFS 框架代码再说别的:
//密码锁上拨一次
public String upone(String s,int i){
char[] ch = s.toCharArray();
if(ch[i] == '9'){
ch[i] = '0';
}else{
ch[i] += 1;
}
return new String(ch);
}
//密码锁向下转一下
public String downone(String s,int i){
char[] ch = s.toCharArray();
if(ch[i] == '0'){
ch[i] = '9';
}else{
ch[i] += 1;
}
return new String(ch);
}
public int bfs(String[] deadends, String target){
Queue<String> q = new LinkedList();
q.offer("0000");
while(!q.isEmpty()){
int sz = q.size();
for(int i = 0;i<sz;i++){
String cur = q.poll();
for(int j = 0;j<4;j++){
String up = upone(cur,j);
String down = downone(cur,j);
q.offer(up);
q.offer(down);
}
}
}
}
这段 BFS 代码已经能够穷举所有可能的密码组合了,但是显然不能完成题目,有如下问题需要解决:
1、会走回头路。比如说我们从 “0000” 拨到 “1000”,但是等从队列拿出 “1000” 时,还会拨出一个 “0000”,这样的话会产生死循环。
2、没有终止条件,按照题目要求,我们找到 target 就应该结束并返回拨动的次数。
3、没有对 deadends 的处理,按道理这些「死亡密码」是不能出现的,也就是说你遇到这些密码的时候需要跳过。
因此,我们根据上面三点去完善这个bfs代码:
class Solution {
public int openLock(String[] deadends, String target) {
return bfs(deadends,target);
}
//密码锁上拨一次
public String upone(String s,int i){
char[] ch = s.toCharArray();
if(ch[i] == '9'){
ch[i] = '0';
}else{
ch[i] += 1;
}
return new String(ch);
}
//密码锁向下转一下
public String downone(String s,int i){
char[] ch = s.toCharArray();
if(ch[i] == '0'){
ch[i] = '9';
}else{
ch[i] += 1;
}
return new String(ch);
}
public int bfs(String[] deadends, String target){
Set<String> deads = new HashSet();
for(String s:deadends){
deads.add(s);
}
Set<String> visited = new HashSet();
Queue<String> q = new LinkedList();
q.offer("0000");
visited.add("0000");
int step = 0;
while(!q.isEmpty()){
int sz = q.size();
for(int i = 0;i<sz;i++){
String cur = q.poll();
if(deads.contains(cur)){
continue;
}
if(cur.equals(target)){
return step;
}
for(int j = 0;j<4;j++){
String up = upone(cur,j);
String down = downone(cur,j);
if(!visited.contains(up)){
q.offer(up);
visited.add(up);
}
if(!visited.contains(down)){
q.offer(down);
visited.add(down);
}
}
}
step++;
}
return -1;
}
}
有一个比较小的优化:可以不需要 dead 这个哈希集合,可以直接将这些元素初始化到 visited 集合中,效果是一样的,可能更加优雅一些。
2.3 滑动谜题
在一个 2 x 3 的板上(board)有 5 块砖瓦,用数字 1~5 来表示, 以及一块空缺用 0 来表示。一次 移动 定义为选择 0 与一个相邻的数字(上下左右)进行交换.
最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。
给出一个谜板的初始状态 board ,返回最少可以通过多少次移动解开谜板,如果不能解开谜板,则返回 -1 。
示例 1:
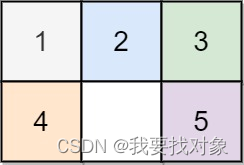
输入:board = [[1,2,3],[4,0,5]]
输出:1
解释:交换 0 和 5 ,1 步完成
示例 2:
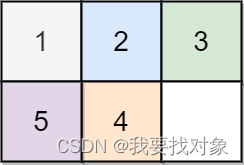
输入:board = [[1,2,3],[5,4,0]]
输出:-1
解释:没有办法完成谜板
示例 3:
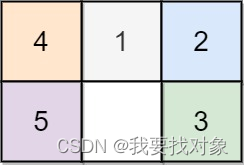
输入:board = [[4,1,2],[5,0,3]]
输出:5
解释:
最少完成谜板的最少移动次数是 5 ,
一种移动路径:
尚未移动: [[4,1,2],[5,0,3]]
移动 1 次: [[4,1,2],[0,5,3]]
移动 2 次: [[0,1,2],[4,5,3]]
移动 3 次: [[1,0,2],[4,5,3]]
移动 4 次: [[1,2,0],[4,5,3]]
移动 5 次: [[1,2,3],[4,5,0]]
思路以及代码:
对于这种计算最小步数的问题,我们就要敏感地想到 BFS 算法。
这个题目转化成 BFS 问题是有一些技巧的,我们面临如下问题:
1、一般的 BFS 算法,是从一个起点 start 开始,向终点 target 进行寻路,但是拼图问题不是在寻路,而是在不断交换数字,这应该怎么转化成 BFS 算法问题呢?
2、即便这个问题能够转化成 BFS 问题,如何处理起点 start 和终点 target?它们都是数组哎,把数组放进队列,套 BFS 框架,想想就比较麻烦且低效。
首先回答第一个问题,BFS 算法并不只是一个寻路算法,而是一种暴力搜索算法,只要涉及暴力穷举的问题,BFS 就可以用,而且可以最快地找到答案。
你想想计算机怎么解决问题的?哪有什么特殊技巧,本质上就是把所有可行解暴力穷举出来,然后从中找到一个最优解罢了。
明白了这个道理,我们的问题就转化成了:**如何穷举出 board 当前局面下可能衍生出的所有局面?**这就简单了,看数字 0 的位置呗,和上下左右的数字进行交换就行了:
这样其实就是一个 BFS 问题,每次先找到数字 0,然后和周围的数字进行交换,形成新的局面加入队列…… 当第一次到达 target 时,就得到了赢得游戏的最少步数。
对于第二个问题,我们这里的 board 仅仅是 2x3 的二维数组,所以可以压缩成一个一维字符串。其中比较有技巧性的点在于,二维数组有「上下左右」的概念,压缩成一维后,如何得到某一个索引上下左右的索引?
对于这道题,题目说输入的数组大小都是 2 x 3,所以我们可以直接手动写出来这个映射:
// neighbor 表示在一维字符串中,索引 i 在二维数组中的的相邻索引
int[][] neighbor = new int[][]{
{1, 3},
{0, 4, 2},
{1, 5},
{0, 4},
{3, 1, 5},
{4, 2}
};
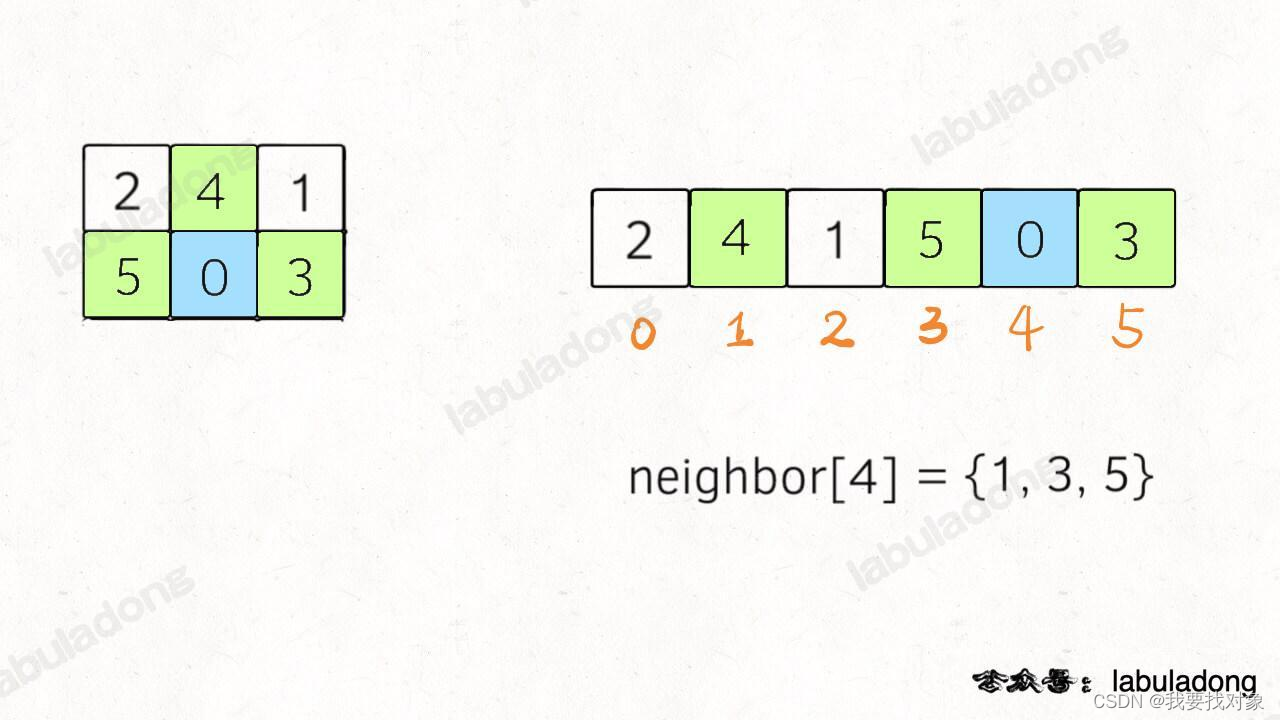
观察上图就能发现,如果二维数组中的某个元素 e 在一维数组中的索引为 i,那么 e 的左右相邻元素在一维数组中的索引就是 i - 1 和 i + 1,而 e 的上下相邻元素在一维数组中的索引就是 i - n 和 i + n,其中 n 为二维数组的列数。
这样,对于 m x n 的二维数组,我们可以写一个函数来生成它的 neighbor 索引映射:
int[][] generateNeighborMapping(int m, int n) {
int[][] neighbor = new int[m * n][];
for (int i = 0; i < m * n; i++) {
List<Integer> neighbors = new ArrayList<>();
// 如果不是第一列,有左侧邻居
if (i % n != 0) neighbors.add(i - 1);
// 如果不是最后一列,有右侧邻居
if (i % n != n - 1) neighbors.add(i + 1);
// 如果不是第一行,有上方邻居
if (i - n >= 0) neighbors.add(i - n);
// 如果不是最后一行,有下方邻居
if (i + n < m * n) neighbors.add(i + n);
// Java 语言特性,将 List 类型转为 int[] 数组
neighbor[i] = neighbors.stream().mapToInt(Integer::intValue).toArray();
}
return neighbor;
}
至此,我们就把这个问题完全转化成标准的 BFS 问题了,借助前文 BFS 算法框架 的代码框架,直接就可以套出解法代码了
class Solution {
public int slidingPuzzle(int[][] board) {
int m = 2, n = 3;
StringBuilder sb = new StringBuilder();
String target = "123450";
// 将 2x3 的数组转化成字符串作为 BFS 的起点
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sb.append(board[i][j]);
}
}
String start = sb.toString();
// 记录一维字符串的相邻索引
int[][] neighbor = new int[][]{/**<extend up -200><div class="img-content"><img src="/algo/images/sliding_puzzle/4.jpeg" class="myimage"/></div> */
{1, 3},
{0, 4, 2},
{1, 5},
{0, 4},
{3, 1, 5},
{4, 2}
};
/******* BFS 算法框架开始 *******/
Queue<String> q = new LinkedList<>();
HashSet<String> visited = new HashSet<>();
// 从起点开始 BFS 搜索
q.offer(start);
visited.add(start);
int step = 0;
while (!q.isEmpty()) {/**<extend up -200><div class="img-content"><img src="/algo/images/sliding_puzzle/3.jpeg" class="myimage"/></div> */
int sz = q.size();
for (int i = 0; i < sz; i++) {
String cur = q.poll();
// 判断是否达到目标局面
if (target.equals(cur)) {
return step;
}
// 找到数字 0 的索引
int idx = 0;
for (; cur.charAt(idx) != '0'; idx++) ;
// 将数字 0 和相邻的数字交换位置
for (int adj : neighbor[idx]) {
String new_board = swap(cur.toCharArray(), adj, idx);
// 防止走回头路
if (!visited.contains(new_board)) {
q.offer(new_board);
visited.add(new_board);
}
}
}
step++;
}
/******* BFS 算法框架结束 *******/
return -1;
}
private String swap(char[] chars, int i, int j) {
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
return new String(chars);
}
}