前言
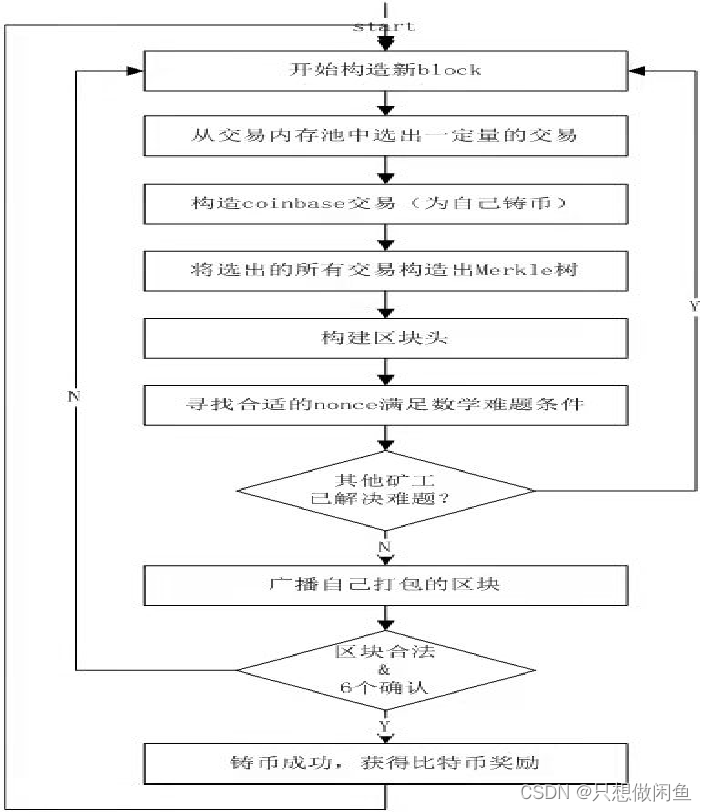
首先我想讲一下,我对多路递归的理解吧,我认为多路递归就是循环中套回调,对于循环有几次就是几叉树,就好比我们常用的二叉树的dfs(node.left) 和 dfs(node.right)等前中后序遍历,也就是for (int i = 0; i < 2; i++) { TreeSet node = i == 0 ? node.left : node.right; dfs(node); }就是一个循环两次的for循环。实在无法理解就画图,好比二叉树画四个方格,1为递归出口,2为左指针,3为右指针,4回溯返回的结果

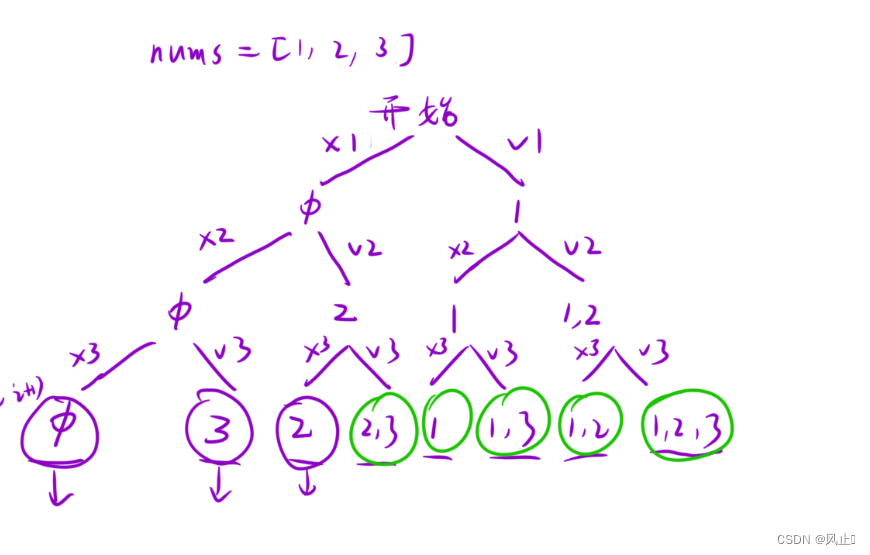
全排列
这一题也就是高中的排列组合,填空问题,n!。第一个空从n个数选一个,第二个空选除第一个空以外的数 n - 1 依次类推

全排列的链接
https://leetcode.cn/problems/VvJkup/![]() https://leetcode.cn/problems/VvJkup/
https://leetcode.cn/problems/VvJkup/
思路分析: 多路递归 + 回溯 + 剪枝 + 引入三个全局变量
多路递归:有几个数树分几个叉
回溯: 归的时候,返回我们修改前的状态
剪枝: 剪掉不需要的,比如遍历了A了下次就不要处理A了
全局变量 result: 返回最终的结果
temp:存放到叶子结点的值
cheak:判断该元素是否枚举过了(剪枝)
这些说明代码注释里面都介绍了!
关于123的全排列的决策树

public class MyTest1 {
private List<List<Integer>> result;
private List<Integer> temp;//存放枚举的结果
private boolean[] cheak;//判断是否已经枚举过了
public List<List<Integer>> permute(int[] nums) {
result = new ArrayList<>();
temp = new ArrayList<>();
cheak = new boolean[nums.length];
dfs(nums);
return result;
}
//深搜(枚举) + 回溯(恢复现场) + 剪枝(cheak变量标记是否不需要遍历)
private void dfs(int[] nums) {
//递归出口
if (temp.size() == nums.length){
result.add(new ArrayList<>(temp));
return;
}
for (int i = 0; i < nums.length; i++) {
if (!cheak[i]) {
temp.add(nums[i]);
cheak[i] = true;
dfs(nums);
//递归完毕,进行回溯的时候说明已经是搞完了再往上返回
//恢复现场
cheak[i] = false;
temp.remove(temp.size() - 1);
}
}
}
}子集
子集就是也是高中数学的基础知识,比如 1 2 的子集是{空集},{1},{2},{1,2},其实就是子序列也就是不去重的子集。

. - 力扣(LeetCode)
思路分析: 这一题主要有两种解法,但是本博客就介绍一种
解法一:双路递归的二叉分为选和不选
全局变量 + 多路递归 + 回溯 没有剪枝(因为只有选不选,不会出现枚举重复元素)
全局变量path: 递了总集的元素次结束,存放
二路递归:选或者不选,来分为二叉树
回溯:选的时候,往上归的时候要恢复现场
注释我都详解了。
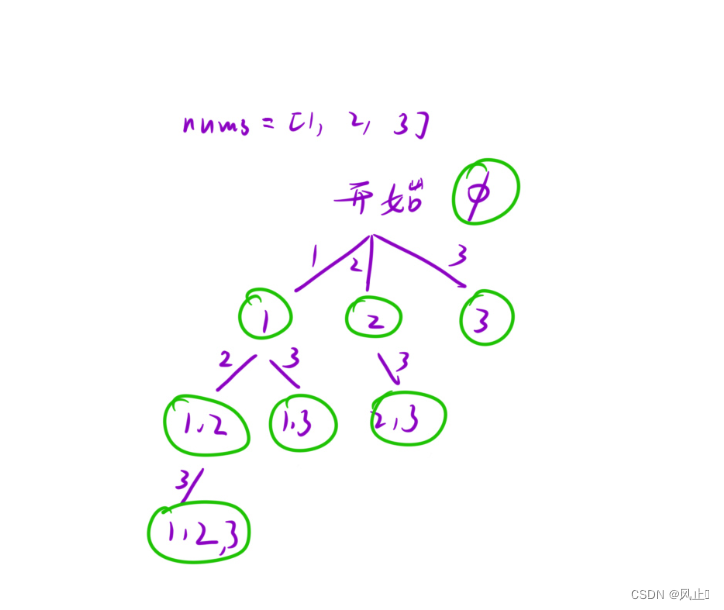
解法二:按照子集个数分,比如空集是个数为0
解法一的决策树
 解法二的决策树
解法二的决策树
注意这是解法一的代码,我并没有写解法二的代码
package study2.day10;
import java.util.ArrayList;
import java.util.List;
//子集
public class MyTest5 {
private List<Integer> path;//定义叶子结点存的内容
private List<List<Integer>> result;//返回值
public List<List<Integer>> subsets(int[] nums) {
path = new ArrayList<>();
result = new ArrayList<>();
dfs(nums, 0);
return result;
}
private void dfs(int[] nums, int index) {
if (index == nums.length) {
result.add(new ArrayList<>(path));
return;
}
// 不选择当前元素
dfs(nums, index + 1);
// 选择当前元素
path.add(nums[index]);
dfs(nums, index + 1);
path.remove(path.size() - 1);//回溯(恢复状态)
}
public static void main(String[] args) {
new MyTest5().subsets(new int[]{1,2,3});
}
}
岛屿数量
岛屿数量也就是抱团1的数量,其中1表示地面,0表示海洋,这个是不是很像围棋,1没有气了就是一个岛了。这个题,其实和我写的博客(腐烂的苹果题目一样)但是我还是写错了,这个和那个唯一的区别,就是那个是同时扩散的bfs,这个是单个遍历的dfs
http://t.csdnimg.cn/q9PFM 这是腐烂苹果博客的链接
思路分析:
解法一:bfs
解法二:dfs
解法一: bfs也就是借助了队列这个数据结构来保证回调的顺序
1.创建一个队列(queue)用来保存回调的顺序
2.遇到 1 入队列,并且标记这个元素已经被扫描过了 vis[i][j] = true
3.队列不为空表示四周有陆地,继续将陆地并且没有被扫描过添加入队列继续遍历
解法二:dfs就是使用让计算机中的栈内存来当一个栈的数据结构供你使用
1.遇到1,进入递归的dfs并且标记为被扫描
2.和上述3一样就不一一介绍了
公共代码都一样只不过是调用的函数不一样:
公共代码
int[] dx = {0, 0, -1, 1};
int[] dy = {1, -1, 0, 0};
boolean[][] vis = null;//判断是否判断过
int m = 0;
char[][] grid = null;
int n = 0;
public int solve (char[][] grid) {
this.grid = grid;
m = grid.length;
n = grid[0].length;
int count = 0;
vis = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (!vis[i][j] && grid[i][j] == '1'){
bfs(vis, i, j);//逐个遍历
count++;
}
}
}
return count;
}解法一代码:
//解法一的bfs代码
private void bfs(boolean[][] vis, int i, int j) {
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{i,j});
vis[i][j] = true;
while(!queue.isEmpty()){
int[] arr = queue.poll();
int a = arr[0], b = arr[1];
for (int k = 0; k < 4; k++) {
int x = a + dx[k], y = b + dy[k];
if (x >= 0 && y >= 0 && x < m && y < n && !vis[x][y] && grid[x][y] == '1'){
queue.offer(new int[]{x, y});
vis[x][y] = true;
}
}
}
}解法二代码:
//深搜,全部的1都搜索
private void dfs(boolean[][] vis, int i, int j) {
vis[i][j] = true;
for (int k = 0; k < 4; k++) {
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && y >= 0 && x < m && y < n && !vis[x][y] && grid[x][y] == '1'){
dfs(vis, x, y);
}
}
}总结
非常感谢您的支持和鼓励!制作博客确实需要付出很多心血,尤其是分享个人经验和解决问题的方法。如果我的回答对您有帮助,我会很高兴为您点个三连。另外,祝您周末愉快,愿您的每一天都充满快乐和成就!