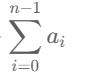'shy'的子序列的个数

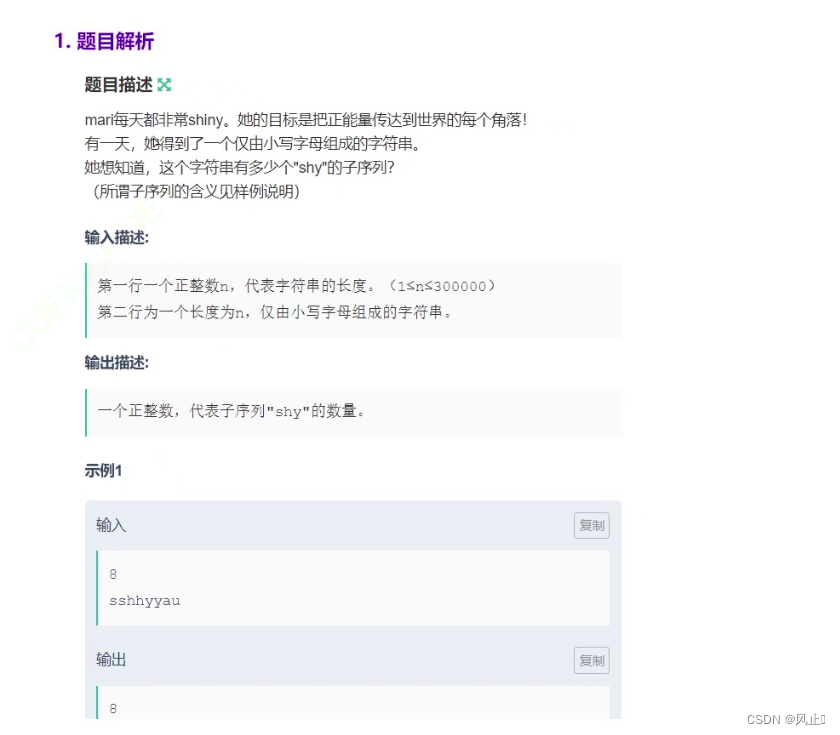
这一题，我一开始就没什么思路，我就开始暴力枚举了，就是定义i，j(找i后面的)，k(找j后面的)，很显然这种方法超时了。所以我就想使用动态规划，但是空间又超了，我就很懵，到最后听老师讲空间优化(使用三个变量(滚动数组))进行优化才解决这道题

 1.暴力枚举

定义: i 指针来找, 找到了s,后在定义 i  + 1 位置为j 指针 找 h，找到定义k指针找y

 public static void main1(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextLine()) { // 注意 while 处理多个 case
            in.nextLine();
            String str = in.nextLine();
            char[] chs = str.toCharArray();
            int count = 0;
            for (int i = 0; i < chs.length; i++) {
                if (chs[i] == 's'){
                    for (int j = i + 1; j < chs.length; j++) {
                        if (chs[j] == 'h') {
                            for (int k = j + 1; k < chs.length; k++) {
                                if (chs[k] == 'y') {
                                    count++;
                                }
                            }
                        }
                    }
                }
            }
            System.out.println(count);
        }
    }

2. 动态规划

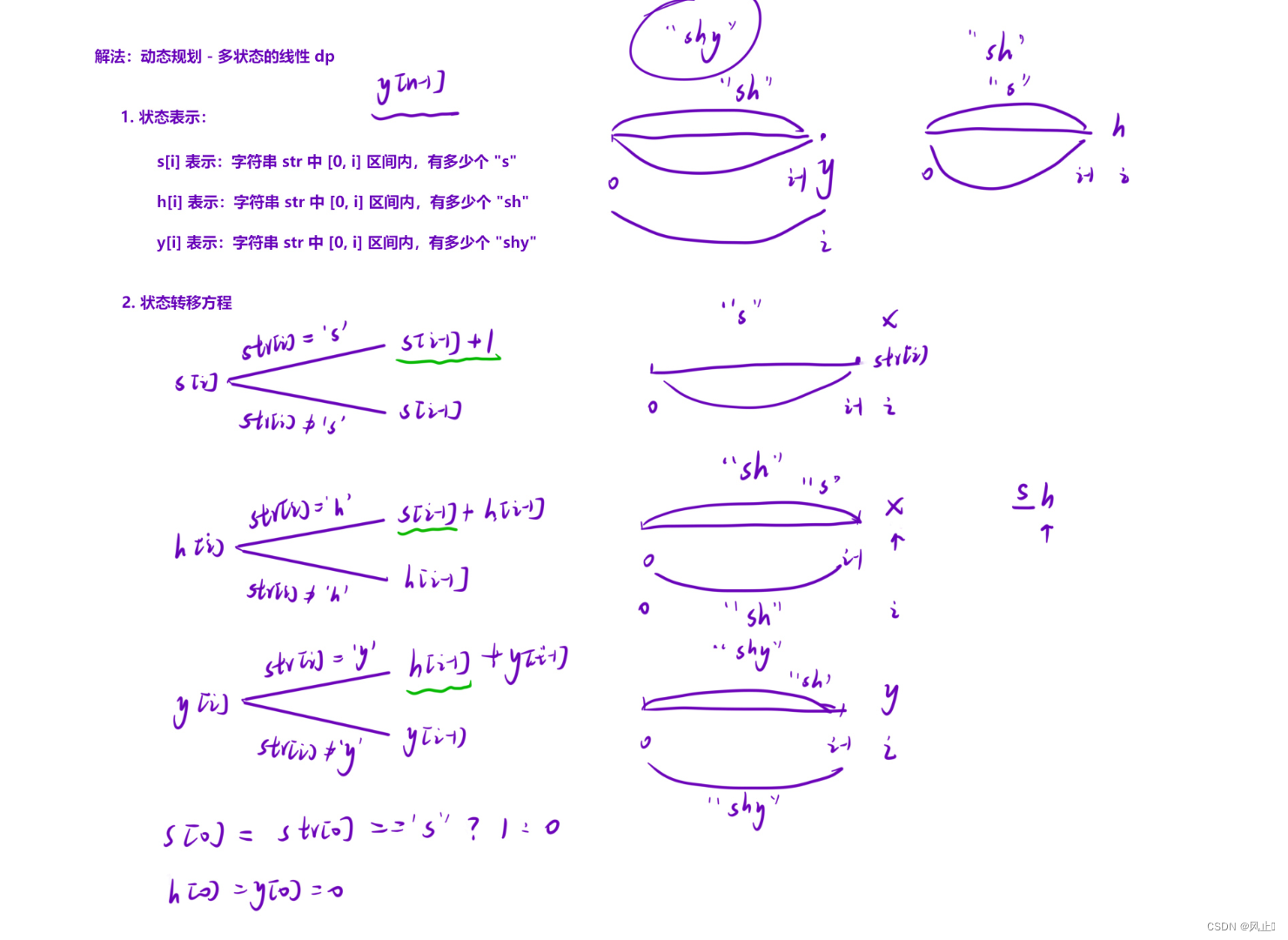
多状态dp表示 的状态表示
1. S[i] 以i位置为结尾的有多少个 'S'
2. H[i] 以i位置为结尾的有多少个 'SH'
3. Y[i] 以i位置为结尾的有多少个 'SHY'

状态转移方程: S[i]     1. i位置为'S'   S[i] = S[i - 1] + 1
                     2. i位置不为'S' S[i] = S[i - 1]
状态转移方程: H[i]     1. i位置为'H'   H[i] = H[i - 1] + S[i - 1]  因为sshh 第四个为h让本来有两个sh + s(h)s(h)的个数
                      2. i位置不为'H' H[i] = H[i - 1]

public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        String str = " " + sc.next();
        int[] s = new int[n + 1];
        int[] h = new int[n + 1];
        int[] y = new int[n + 1];
        char[] chs = str.toCharArray();
        for (int i = 1; i < chs.length; i++) {
            if (chs[i] == 's'){
                s[i] = s[i - 1] + 1;
                h[i] = h[i - 1];
                y[i] = y[i - 1];
            }else if (chs[i] == 'h'){
                h[i] = h[i - 1] + s[i - 1];
                s[i] = s[i - 1];
                y[i] = y[i - 1];
            } else if (chs[i] == 'y') {
                y[i] = y[i - 1] + h[i - 1];
                s[i] = s[i - 1];
                h[i] = h[i - 1];
            }else {
                s[i] = s[i - 1];
                h[i] = h[i - 1];
                y[i] = y[i - 1];
            }
        }
        System.out.println(y[n]);
    }

3.空间优化 

使用三个变量进行优化，因为只需要用到前面一个状态，其他状态都不需要，这样也不需要不处理，不为s位置设置为s[i] = s[i - 1]，因为等于和不处理一样，这就像求斐波那契一样。

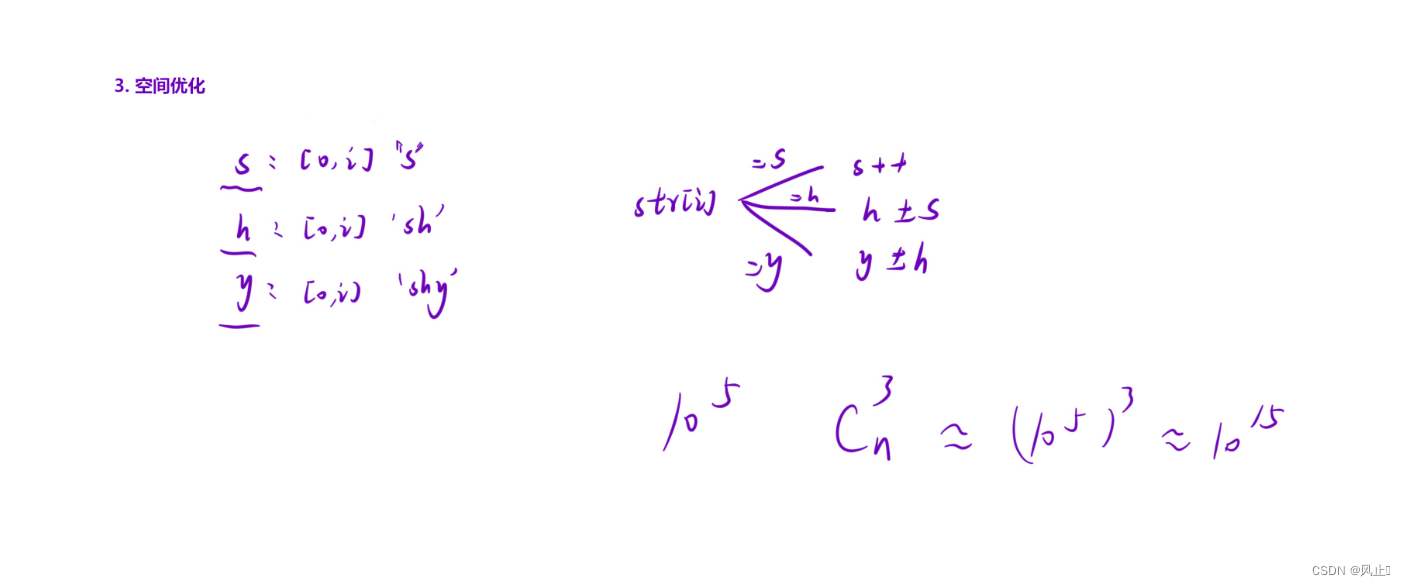
public static void main3(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        String str = " " + sc.next();
        int s = 0, h = 0, y = 0;
        char[] chs = str.toCharArray();
        for (int i = 1; i < chs.length; i++) {
            if (chs[i] == 's') {
                s += 1;
            } else if (chs[i] == 'h') {
                h += s;
            } else if (chs[i] == 'y') {
                y += h;
            }
        }
    }