C 函数递归

news2025/1/17 22:05:23

什么是递归

递归的限制条件

递归的例子

1、用递归求n的阶乘

递归扩展学习

1、青蛙跳台阶

思路

代码实现

2、汉诺塔问题

思路

代码实现

总结

什么是递归

递归：“递推” + “回归”

在C语言中，函数递归就是：函数自己调用自己

将一件事情 “大事化小”，完成这些小事所用的方法都是相同的，只是参数不一样。

递归的限制条件

递归存在限制条件，当满足这个限制条件的时候，递归便不再继续。
每次递归调用之后越来越接近这个限制条件。

递归的例子

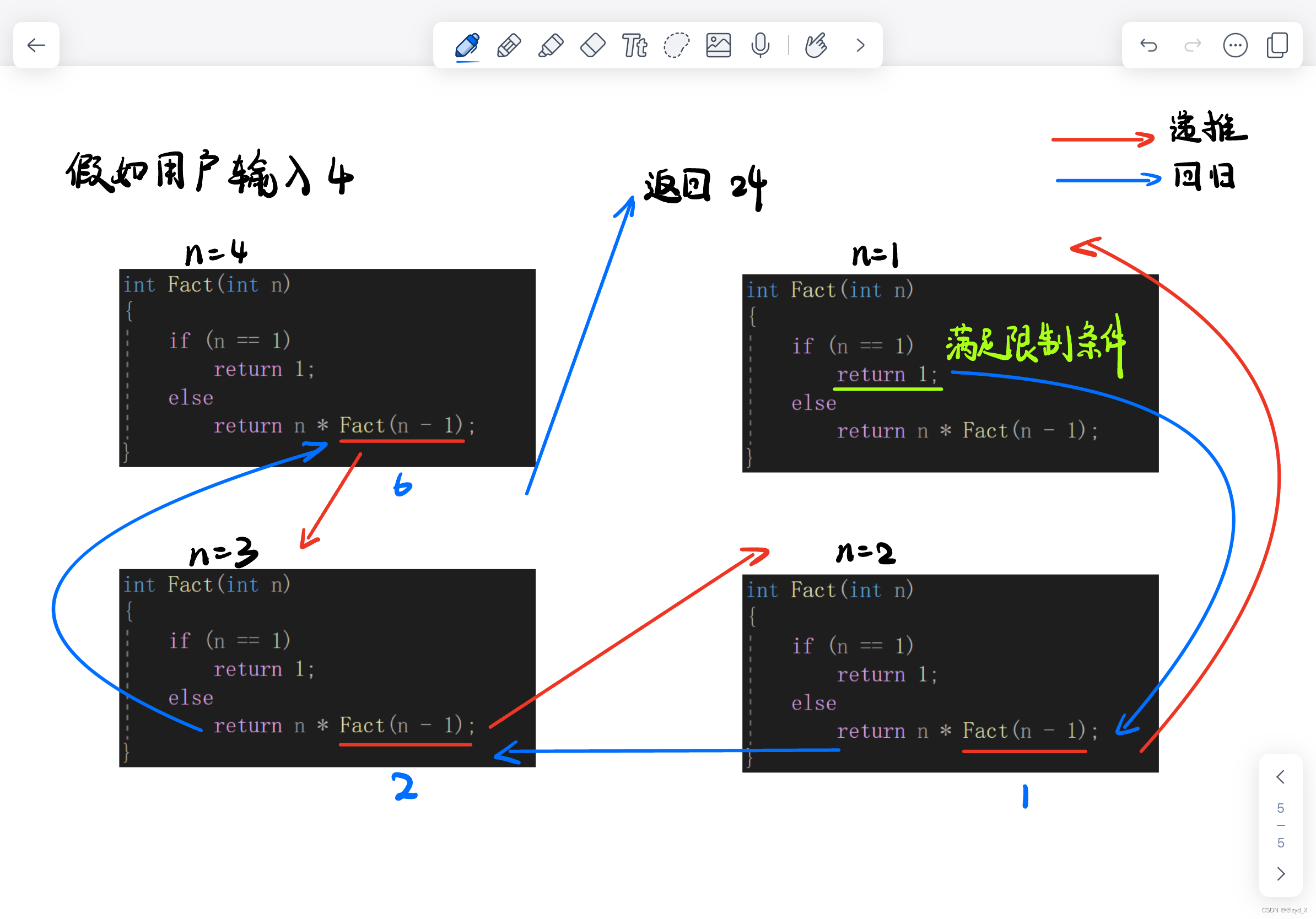
1、用递归求n的阶乘

//VS2022 x64    
#include<stdio.h>
int Fact(int n)    //实现阶乘的函数
{
	if (n == 0)       //限制条件
		return 1;
	else
		return n * Fact(n - 1);    //递归    
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fact(n);       
	printf("%d\n", ret);        
	return 0;
}

递归扩展学习

1、青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

思路

可以发现，跳到第n个台阶，最后一步，只有两种方法：

从第 n-1 个楼梯跳上一级台阶；
从第 n-2 个楼梯跳上两级台阶；

代码实现

#include<stdio.h>
int Jump(int n)
{
	if (n == 1)
		return 1;
	else if (n == 2)
		return 2;
	else
		return Jump(n - 1) + Jump(n - 2);
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int sum = Jump(n);
	printf("小青蛙有 %d 种跳法到第 %d 台阶", sum, n);
	return 0;
}

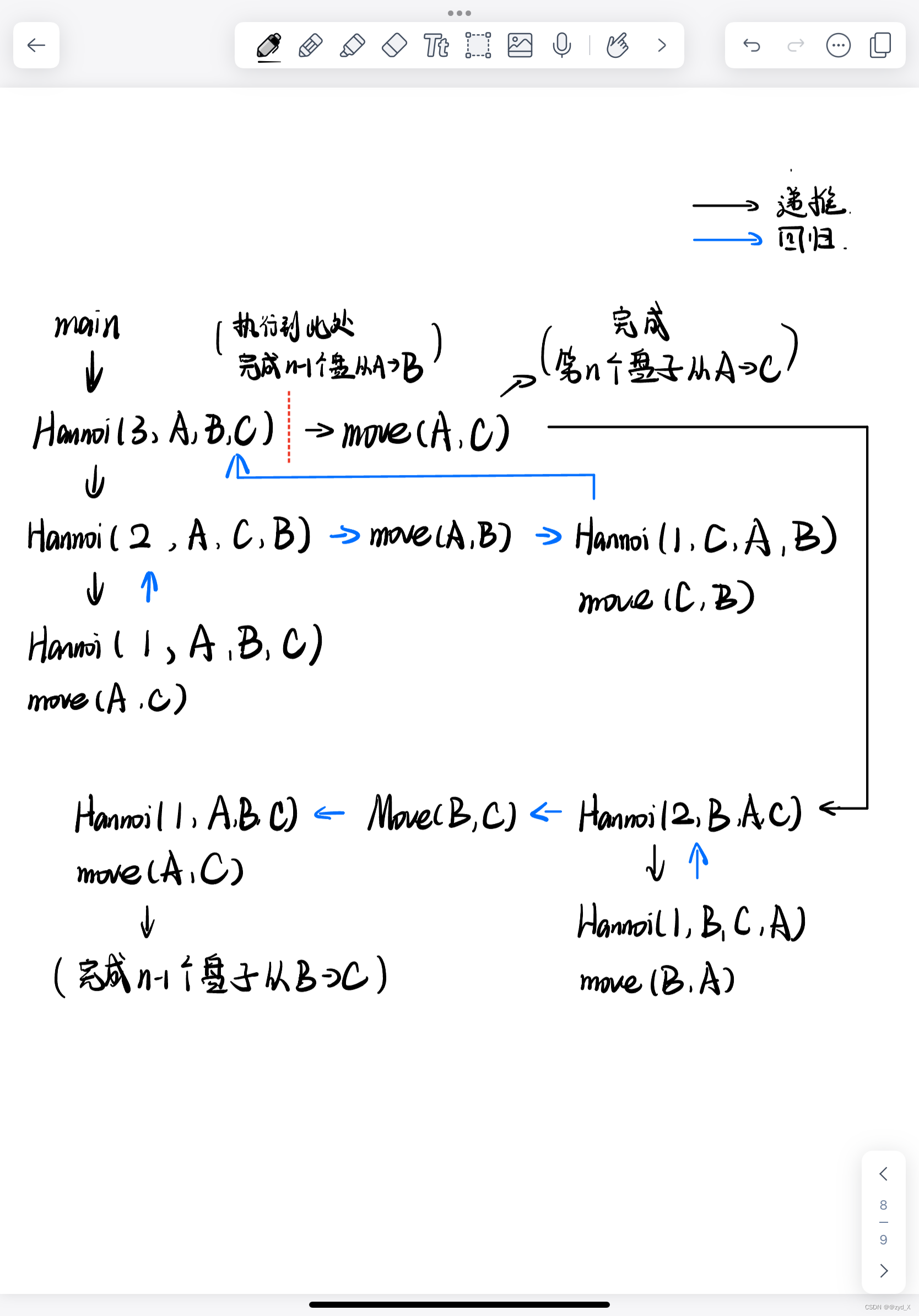
2、汉诺塔问题

给定三根柱子，记为 A,B,C，其中 A 柱子上有 n 个盘子，从上到下编号为 0 到 n−1 ，且上面的盘子一定比下面的盘子小。问：将 A 柱上的盘子经由 B 柱移动到 C 柱最少需要多少次？打印出每个步骤

移动时应注意：

一次只能移动一个盘子
 大的盘子不能压在小盘子上

思路

先从简单的三个盘子试试，可以先不看答案自己画一画，挺好玩的，注意规则噢

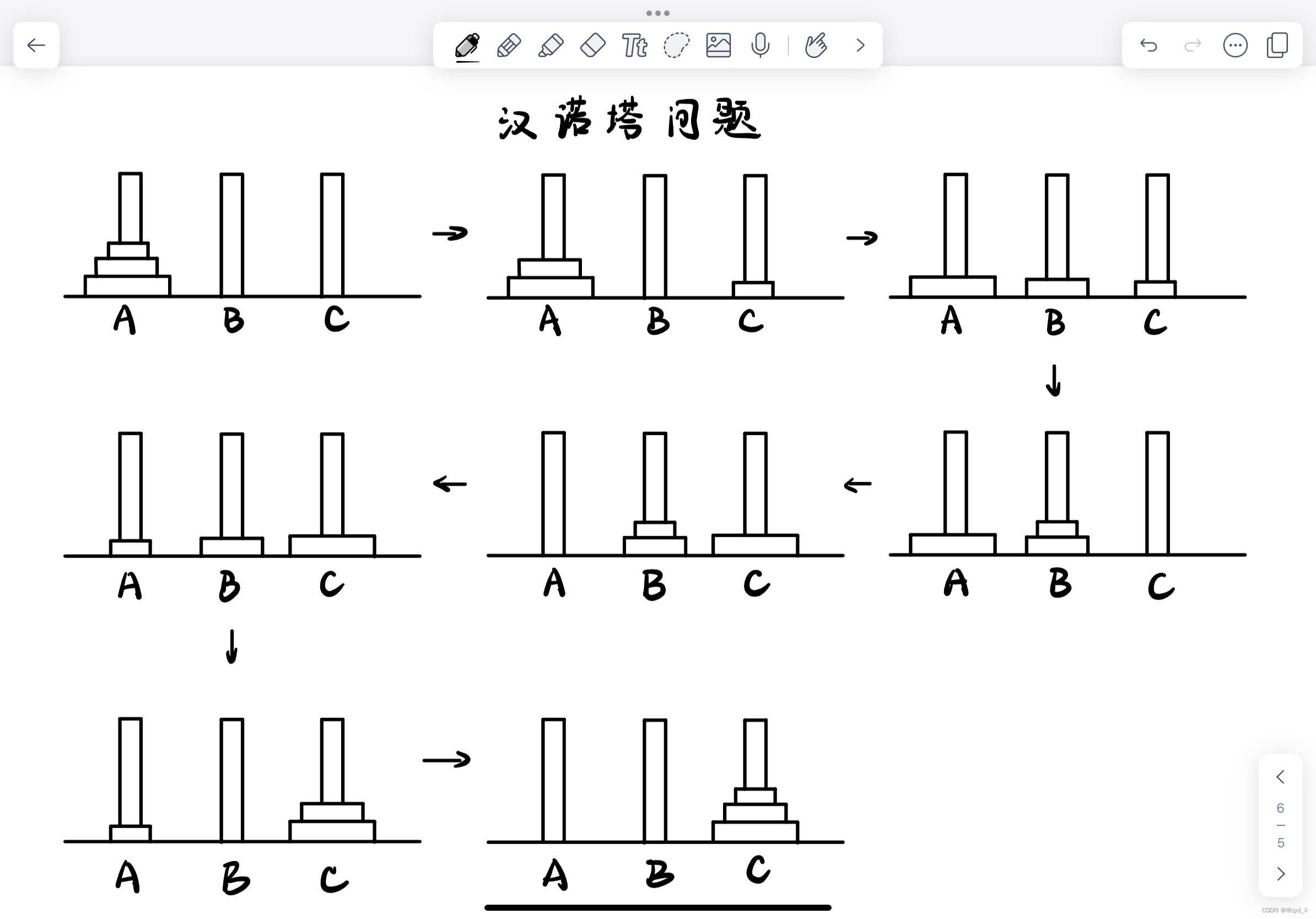
（1）n个盘子从A柱到C柱最少移动次数

（2）打印出每个步骤

代码实现

#include<stdio.h>
void Move(char pos1, char pos2)		//打印步骤
{
	printf(" %c->%c ", pos1, pos2);
}

//pos1 起点
//pos2 中转站
//pos3 目的地
void Hannoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1)
		Move(pos1, pos3);	
	else
	{
		Hannoi(n - 1, pos1, pos3, pos2);	//n-1个盘子借助 pow3 从 pow1->pow2
		Move(pos1, pos3);				//第n个盘子从 pos1 -> pos3
		Hannoi(n - 1, pos2, pos1, pos3);	//n-1个盘子借助 pos1 从 pos2->pos3
	}
}

int main()
{
	int n = 0;	//需要移动的盘子数量
	scanf("%d", &n);
	Hannoi(n, 'A', 'B', 'C');
	return 0;
}