一、理论基础
TSP(traveling salesman problem,旅行商问题)是典型的NP完全问题,即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长,到目前为止还未找到一个多项式时间的有效算法。TSP问题可描述为:已知n个城市相互之间的距离,某一旅行商从某个城市出发访问每个城市有且仅有一次,最后回到出发城市,如何安排才使其所走路线距离最短。简言之,就是寻找一条最短的遍历n个城市的路径。
二、案例背景
1,问题描述
本案例以14个城市为例,假定14个城市的位置坐标如表1所列。寻找出一条最短的遍历14个城市的路径。

2,解决思路和步骤
(1).算法流程
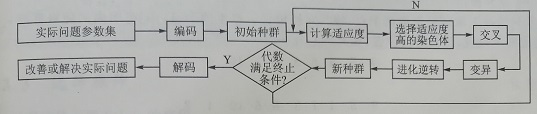
遗传算法TSP问题的流程图如图1所示。
图1 遗传算法TSP问题求解的流程图
<1>编码
采用整数排列编码方法。对于n nn个城市的TSP问题,染色体分为n nn段,其中每一段为对应城市的编号,对10个城市的TSP问题1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 {1,2,3,4,5,6,7,8,9,10}1,2,3,4,5,6,7,8,9,10,则∣ 1 ∣ 10 ∣ 2 ∣ 4 ∣ 5 ∣ 6 ∣ 8 ∣ 7 ∣ 9 ∣ 3 |1|10|2|4|5|6|8|7|9|3∣1∣10∣2∣4∣5∣6∣8∣7∣9∣3就是一个合法的染色体。
<2>种群初始化
在完成染色体编码以后,必须产生一个初始种群作为起始解,所以首先需要决定初始化种群的数目。初始化种群的数目一般根据经验得到,一般情况下种群的数量视城市规模的大小而定,其取值在50~200之间浮动。
<3>适应度函数

即适应度函数为恰好走遍n nn个城市再回到出发城市的距离的倒数。优化的目标就是选择适应度函数值尽可能大的染色体,适应度函数值越大的染色体越优质,反之越劣质。
<4>选择操作
选择操作即从旧群体中以一定概率选择个体到新群体中,个体被选中的概率跟适应度值有关,个体适应度值越大,被选中的概率越大。
<5>交叉操作
采用部分映射杂交,确定交叉操作的父代,将父代样本两两分组,每组重复以下过程(假定城市数为10):

<6>变异操作

<7>进化逆转操作
为改善遗传算法的局部搜索能力,在选择、交叉、变异之后引进连续多次的进化逆转操作。这里的“进化”是指逆转算子的单方向性,即只有经过逆转后,适应度值有提高的才接受下来,否则逆转无效。

对每个个体进行交叉变异,然后代入适应度函数进行评估,x xx选择出适应度值大的个体进行下一代的交叉和变异以及进化逆转操作。循环操作:判断是否满足设定的最大遗传代数MAXGEN ,不满足则跳入适应度值的计算;否则,结束遗传操作。
3.仿真结果为:
优化前的一个随机路线轨迹图如图2所示。

优化后的路线图如图3所示。

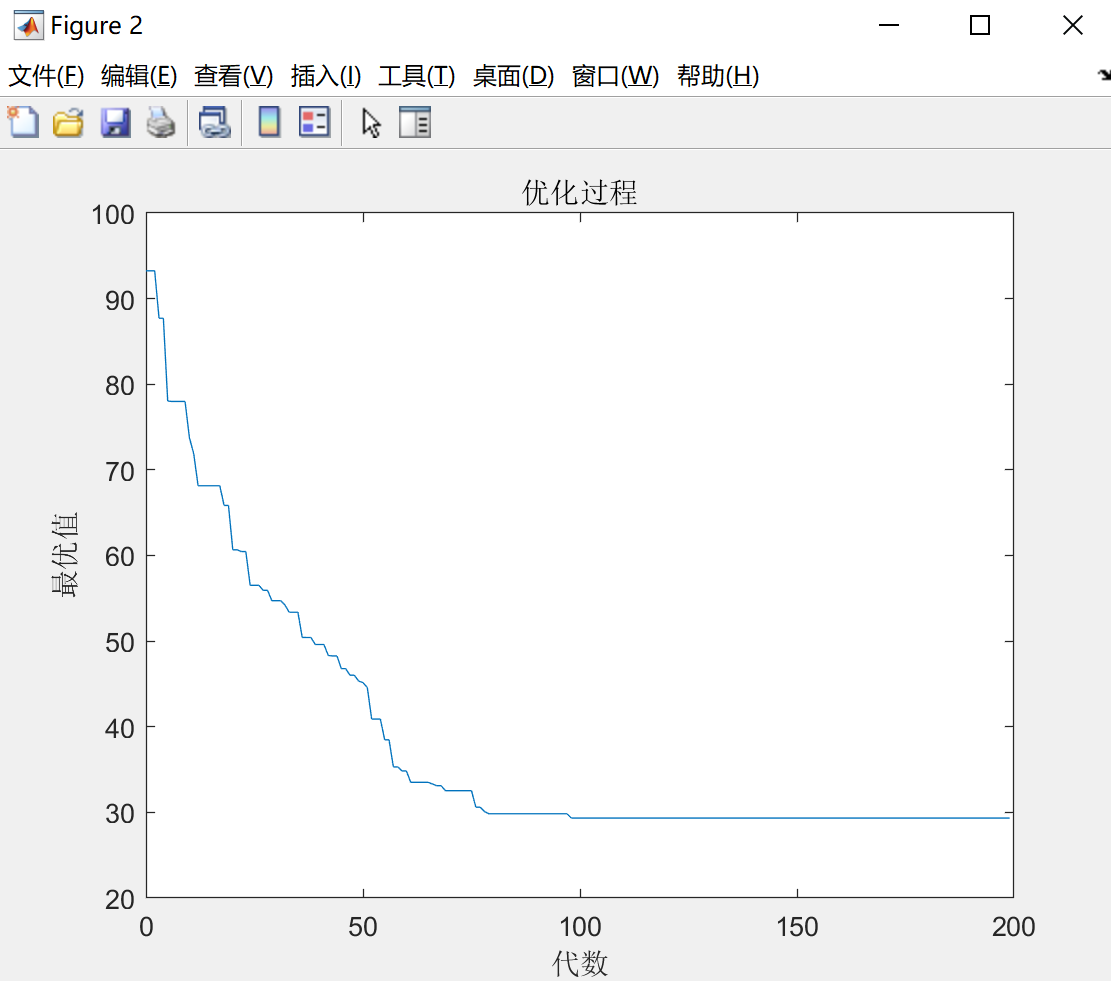
优化迭代图如图4所示。