P1、什么是并查集
引用自百度百科:
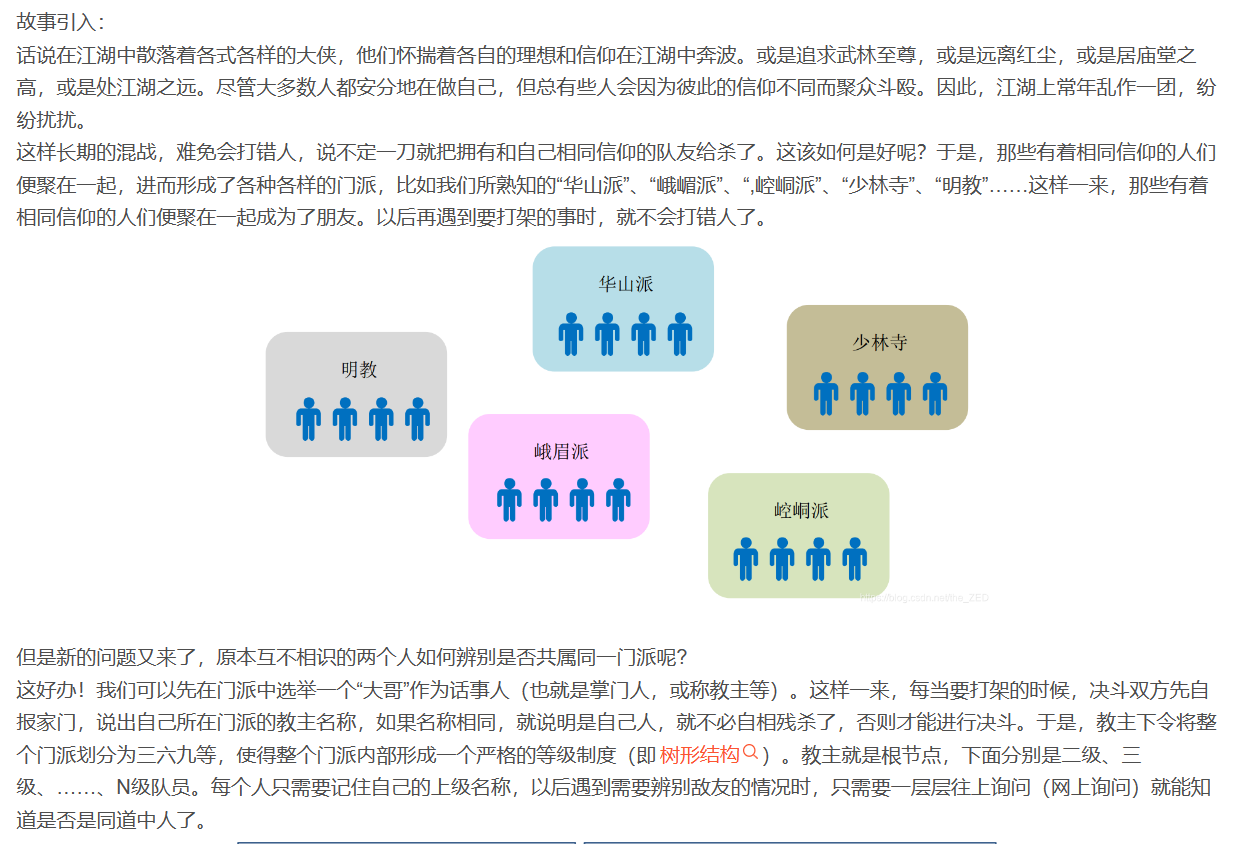
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。常常在使用中以森林来表示。
简单来说,并查集是一种以树形结构来表示不同种类数据的集合。一般当我们需要用到数据的连通性时会用到它。
并查集维护一个数组parent,parent数组中维护的不是元素本身,而是元素的下标索引,当然,这个下标索引是指向该元素的父元素的。
引用自:【算法与数据结构】—— 并查集-CSDN博客
P2、简单、无优化的并查集
// 未改进版本
public class Djset {
private int[] parent; // 记录节点的根
public Djset(int n) {
for (int i = 0; i < n; i++)
parent[i] = i;
}
public int find(int x) {
if (x != parent[x]) return find(parent[x]);
return parent[x];
}
public void merge(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootX != rootY) {
parent[rootY] = rootX;
}
}
}
这种没有任何优化的并查集,比较简单,但是效率很低。为什么?
问题1:
当合并两个节点时,这里是没有任何判断的,便直接将rootx设置成了rooty的父节点。
假如rooty的叶子节点深度比rootx的叶子节点深度大呢?此时,树的深度会持续增加,会造成后续的节点查询时间长。
问题2:
在寻找某个节点的根节点的过程中,我们也未对其父节点和祖父节点…等作任何操作。
假如该节点会被合并(merge)很多次,而每次都要经过父节点、祖父节点…层层寻找,造成了不必要的时间浪费。
比如:
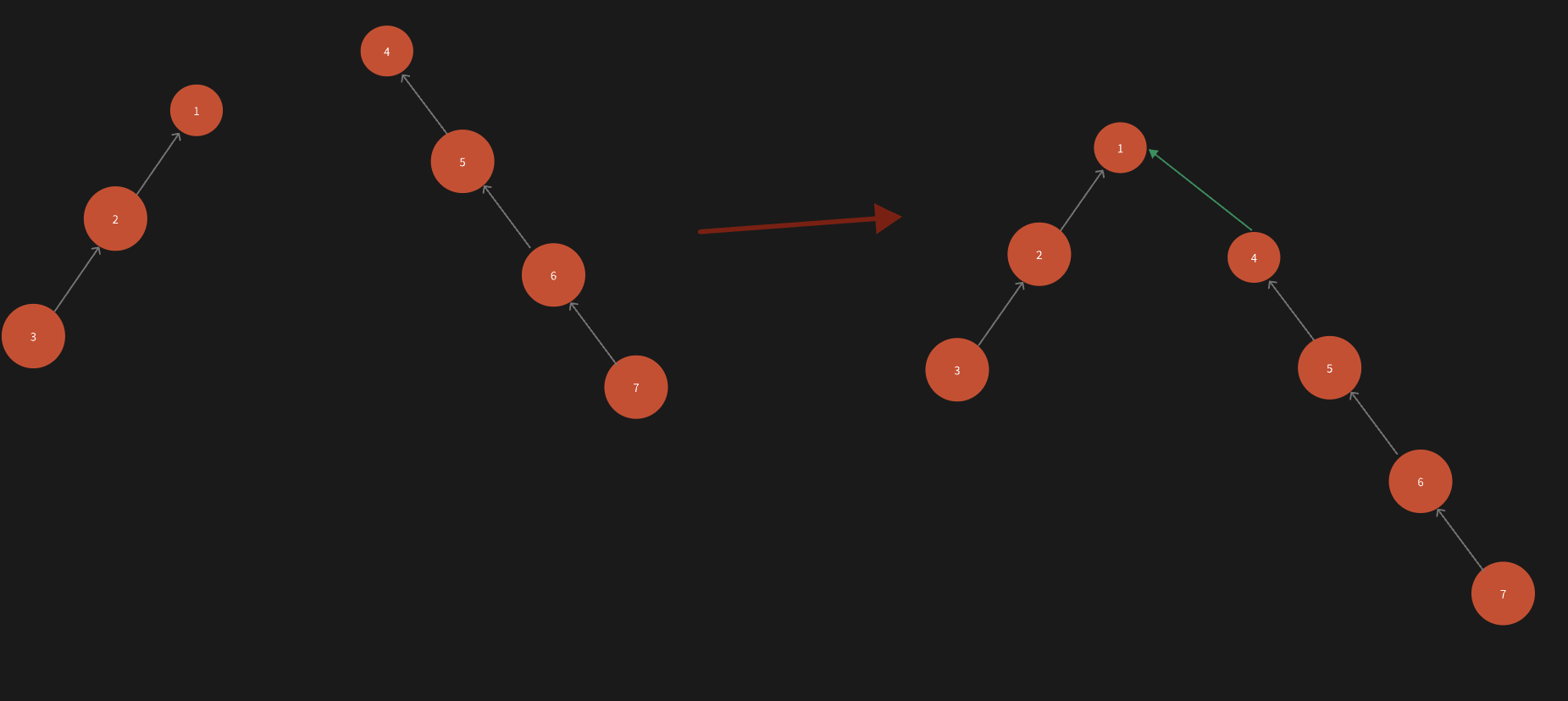
这样,树的深度便在无形之中增加了1。
如果反过来,将rootx的父节点设置为rooty,看下效果:
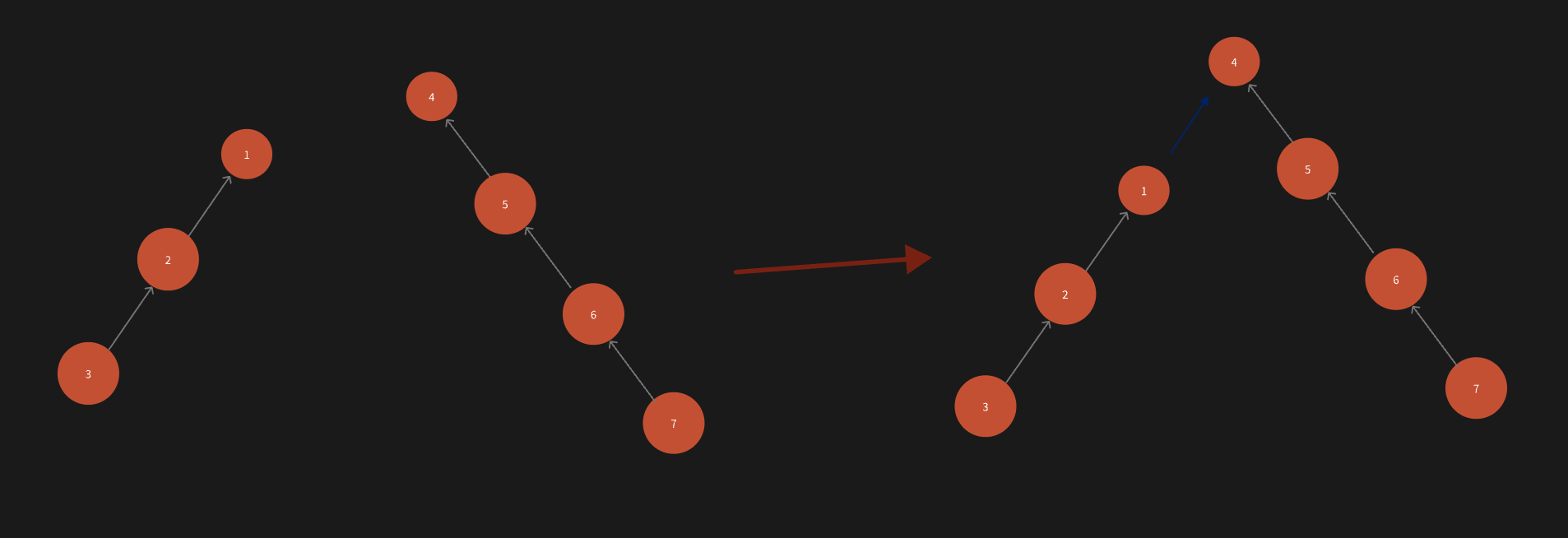
树的深度是没有增加的,不会对后续节点造成影响。
P3、优化后的并查集【按秩合并】【路径压缩】
// 注意:使用该代码,并不能使得所有的元素都直接指向根节点,仍然存在间接的指向
public class Djset {
private int[] parent; // 记录节点的根
private int[] rank; // 记录根节点的深度,优化合并操作
// 构造函数,初始化每个节点的根为其自身,并设置初始秩为0
public Djset(int n) {
parent = new int[n];
rank = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
rank[i] = 1; // 确保初始化每个节点的初始秩也为1
}
}
// 查找x的根节点,同时进行路径压缩
public int find(int x) {
if (x != parent[x]) {
parent[x] = find(parent[x]); // 路径压缩至根节点
}
return parent[x];
}
// 合并x和y所在的集合,按秩合并优化
public void merge(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
// 按秩合并:将秩较小的集合合并到较大的集合
if (rank[rootX] < rank[rootY]) {
int temp = rootX;
rootX = rootY;
rootY = temp;
}
parent[rootY] = rootX; // 根据秩决定合并方向
if (rank[rootX] == rank[rootY]) {
rank[rootX]++;
}
}
}
}
这里主要针对未改进的版本,做了两点优化 【按秩合并】和【路径压缩】
① 按秩合并
好的,让我们先弄清楚什么是按秩合并
秩:我们暂时将其定义为节点的最大深度(从节点自身开始,到叶子节点的最大深度)
按秩合并:主要是针对merge函数,在合并两个集合时,将秩大的根节点设置为秩小的根节点的父节点。意思是当要合并两个根节点A、B时,如果节点A的秩大于节点B的秩,那么将节点A设置为节点B的父节点,反之亦然。
比如:
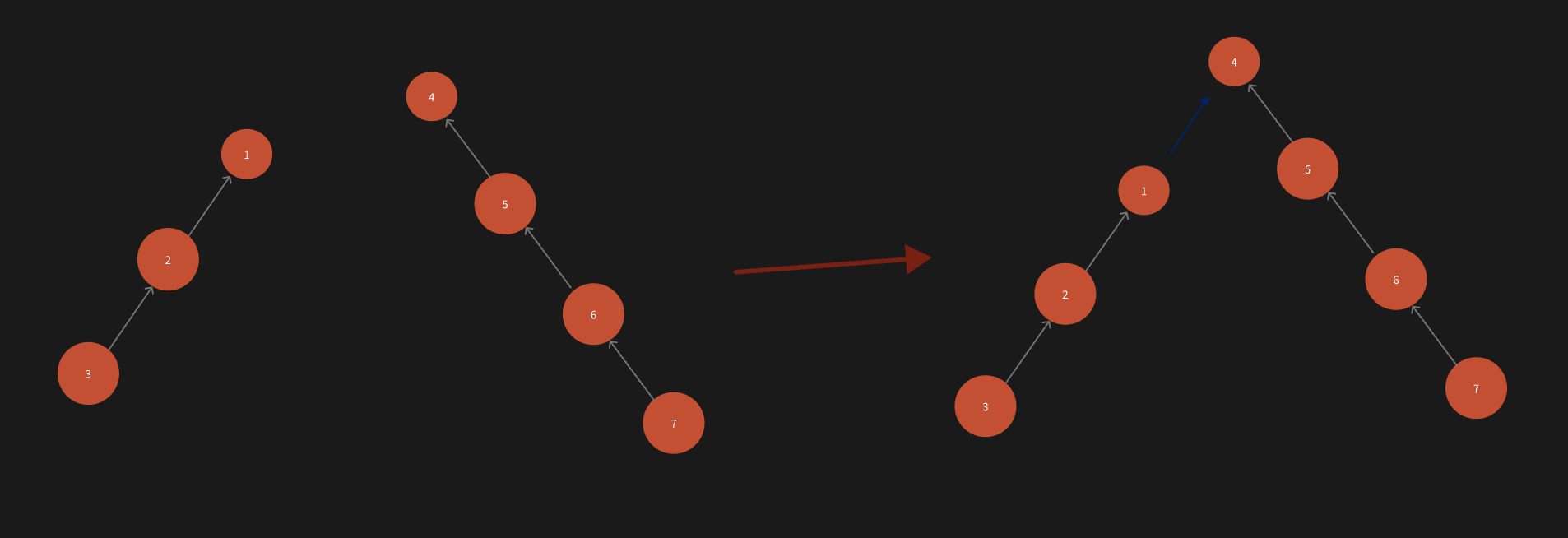
通过将秩大的根节点设置为合并后的根节点,避免了树的深度增加。
② 路径压缩
同样,先弄清楚什么是路径压缩
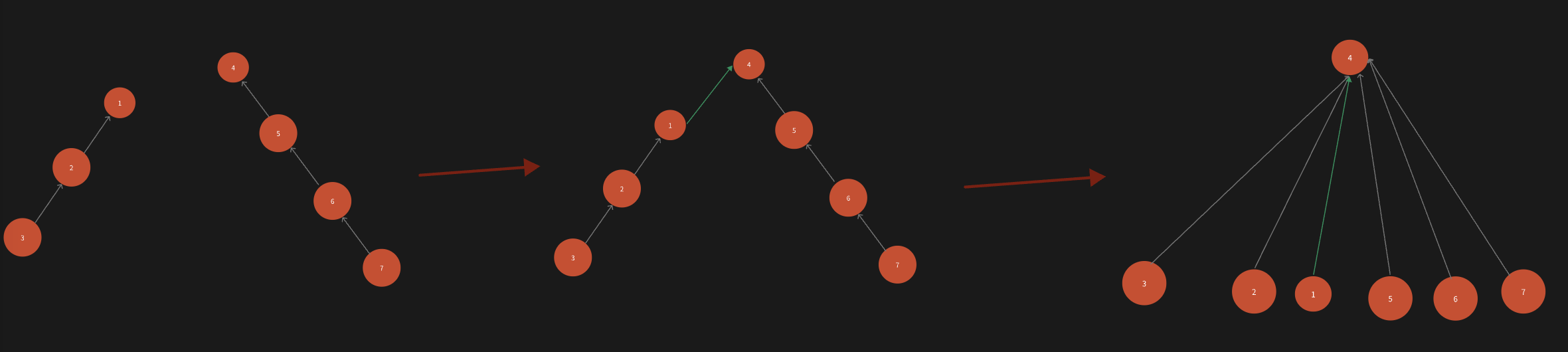
路径压缩:主要针对find函数,当在寻找一个节点A的根节点root时,直接将节点A的父节点B、祖父节点C…等节点全部指向根节点root。
优点:这样在下次寻找A的根节点、B的根节点、C的根节点时可以节省很长一段搜索路径。
如:
接下来,来几个简单的困难题:
原题链接:
839. 相似字符串组 - 力扣(LeetCode)
这个题目首先要理解相似的定义:
两个字符串相似的含义是能够通过交换两个字符的位置,得到另外一个字符串。
根据题目来看,给的字符串中的字母是相同的,不同的顺序,那么相似只有两种情况:两个字符串的对应位置中只有 0 个或者 2 个不同。
我们将字符串看作节点,两重 for 循环,实现对节点之间两两组合,判断两个节点是否相似,判断相似的方法是:
两个字符串的对应位置中只有 0 个或者 2 个不同;
如果两个字符串相似则将他们归入一组,之后遍历时,如果不是同一组就需要进行判断。
初始化并查集数组,并初始化集合数,每次合并减一。
class Solution {
public static int[] father = new int[10000];
public static int sets;
public static void build(int n) {
for (int i = 0; i < n; i++) {
father[i] = i;
}
sets = n;
}
public static int find(int i) {
if (i != father[i]) {
father[i] = find(father[i]);
}
return father[i];
}
public static void union(int x, int y) {
int fx = find(x);
int fy = find(y);
if (fx != fy) {
father[fx] = fy;
sets--;
}
}
public int numSimilarGroups(String[] strs) {
int n = strs.length;
int m = strs[0].length();
build(n);
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (find(i) != find(j)) {
int diff = 0;
for (int k = 0; k < m && diff < 3; k++) {//不同之处大于三那就没有意义了,一定不相似
if (strs[i].charAt(k) != strs[j].charAt(k)) {
diff++;
}
}
if (diff == 0 || diff == 2) {
union(i, j);
}
}
}
}
return sets;
}
}
原题链接:
765. 情侣牵手 - 力扣(LeetCode)

首先,我们总是以「情侣对」为单位进行设想:
当有两对情侣相互坐错了位置,ta们两对之间形成了一个环。需要进行一次交换,使得每对情侣独立(相互牵手)

如果三对情侣相互坐错了位置,ta们三对之间形成了一个环,需要进行两次交换,使得每对情侣独立(相互牵手)

如果四对情侣相互坐错了位置,ta们四对之间形成了一个环,需要进行三次交换,使得每对情侣独立(相互牵手)
也就是说,如果我们有 k 对情侣形成了错误环,需要交换 k - 1 次才能让情侣牵手。
于是问题转化成 n / 2 对情侣中,有多少个这样的环。
如果他们本来就是情侣,他们处于大小为1的错误环中,只需要交换0次。
如果不是情侣,说明他们呢两对处在同一个错误环中,我们将他们合并,将所有的错坐情侣合并后,答案就是情侣对 - 环个数。
class Solution {
public int minSwapsCouples(int[] row) {
int n = row.length;
bulid(n / 2);
for (int i = 0; i < n; i += 2) {
union(row[i] / 2, row[i + 1] / 2);
}
return n / 2 - set;
}
//首先计算数组长度的一半(即情侣对数),然后调用bulid方法初始化并查集,
//之后遍历数组,对每一对执行union操作合并它们所在的集合。
// 最后,返回初始集合数量减去最终集合数量的结果,即为最少需要交换的次数。
public static int[] father = new int[100];
public static int set;
public static void bulid(int x) {
set = x;
for (int i = 0; i < x; i++) {
father[i] = i;
}
}
public static int find(int i){
if(i==father[i])return father[i];
else return find(father[i]);
}
public static void union(int x,int y){
if(find(x)!=find(y)){
father[find(x)]=find(y);
set--;
}
}
}