题目地址
1. 思路
1.1 基本思路及假设
拿到这个题,首先想到,这是类似删除元素的方法,因为删除元素也是移动元素,但是移动的方向和删除元素的方法刚好相反,我们都知道,如果在数组中删除某个元素,其方法是向前逐渐覆盖这个要删除的元素的位置,也就是从右向左移动覆盖,但是这次我们要把需要移动的0依次向右移动,而我们之前写过的【代码随想录刷题记录】LeetCode27移除元素是类似的思路,我们只需要魔改LeetCode27移除元素的代码,它的代码如下:
class Solution {
public:
// 引用传递,直接改nums,是改其本身,不是拷贝
int removeElement(vector<int>& nums, int val) {
int slow = 0; //慢指针,用来记录删除该元素后,每个元素对应的新下标slow
for(int fast = 0; fast < nums.size(); fast++)
{
if(val != nums[fast])
{
// 下一次循环必须先执行赋值操作再进行slow的自增
nums[slow] = nums[fast];
slow++;
}
}
return slow;
}
};
我们需要修改for循环的if条件来达到遇到0就移动的目的,也就是将if(val != nums[fast])转换为if(nums[fast] != 0),然后我们思考一下,if条件里面的逻辑是逐渐从右向左移动覆盖,我们要将其改成从左向右移动,具体if条件里该写什么,我们写一个简单的例子试一试(这里假设我们的if条件写的东西还不知道是什么):
假设有数组nums[2,0,2]

fast=0:

由于
nums
[
fast
]
=
nums
[
0
]
=
2
≠
0
\text{nums}[\text{fast}]=\text{nums}[0]=2\ne0
nums[fast]=nums[0]=2=0则,进入if条件,因为slow和fast指向的都是同一个元素,我们还是不知道到底该写什么样的逻辑才能从左向右不覆盖式地移动元素,这里似乎用nums[slow]=nums[fast]也可以,并且在不等的条件下,slow是要自增的,我们假设做了上述操作,继续下一次循环:
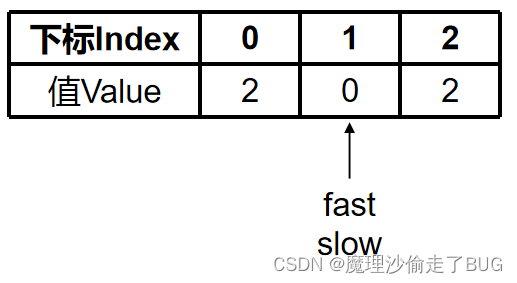
fast=1:
由于
nums
[
fast
]
=
nums
[
1
]
=
0
=
0
\text{nums}[\text{fast}]=\text{nums}[1]=0=0
nums[fast]=nums[1]=0=0则,此时,找到了0,为了能移动,slow不再自增,fast继续自增,没有进入if条件,继续下一次循环:
fast=2:

由于
nums
[
fast
]
=
nums
[
2
]
=
2
≠
0
\text{nums}[\text{fast}]=\text{nums}[2]=2\ne0
nums[fast]=nums[2]=2=0则,进入if条件,现在我想让0移动到最后,就需要让slow和fast指向的元素互换位置,我们大胆假设这是对的,并写出了如下代码:
class Solution {
public:
void moveZeroes(vector<int>& nums) {
//模仿O(n)的删除数组元素的方法删除0
//if条件由nums[fast]!=val改成nums[fast]!=0
//但是这次不是仅仅nums[slow]=nums[fast],而是将它们两个交换
int slow = 0;
int temp = 0;//临时变量存储交换值
for(int fast = 0; fast < nums.size(); fast++)
{
if(nums[fast]!=0)
{
//交换元素位置
temp = nums[slow];
nums[slow] = nums[fast];
nums[fast] = temp;
slow++;
}
}
}
};
1.2 算法的基本情况
由于我们是从左向右移动元素,那么就分为3个情况
- 0在末尾(此时不需要移动)
- 0不在末尾
- 数组中没有0
1.3 验证假设
1.3.1 0在末尾(此时不需要移动)
假设数组nums[2,3,0]:
fast=0:

由于
nums
[
fast
]
=
nums
[
0
]
=
2
≠
0
\text{nums}[\text{fast}]=\text{nums}[0]=2\ne0
nums[fast]=nums[0]=2=0则交换slow和fast指向的元素(指向同一个元素,相当于没换),slow自增
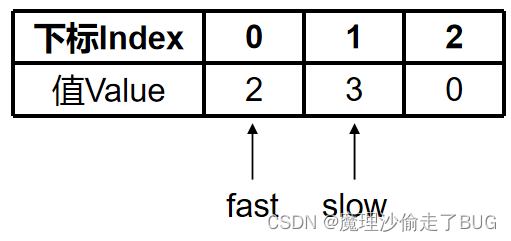
fast=1:

由于
nums
[
fast
]
=
nums
[
1
]
=
3
≠
0
\text{nums}[\text{fast}]=\text{nums}[1]=3\ne0
nums[fast]=nums[1]=3=0则交换slow和fast指向的元素(指向同一个元素,相当于没换),slow自增

fast=2:

由于
nums
[
fast
]
=
nums
[
3
]
=
0
=
0
\text{nums}[\text{fast}]=\text{nums}[3]=0=0
nums[fast]=nums[3]=0=0则什么都不做,退出循环
最后结果还是[2,3.0]
结果正确
1.3.2 0不在末尾
假设数组nums[0, 2, 0, 3]:
fast=0:

由于
nums
[
fast
]
=
nums
[
0
]
=
0
=
0
\text{nums}[\text{fast}]=\text{nums}[0]=0=0
nums[fast]=nums[0]=0=0则什么都不做,进入下一次循环
fast=1:

由于
nums
[
fast
]
=
nums
[
1
]
=
2
≠
0
\text{nums}[\text{fast}]=\text{nums}[1]=2\ne0
nums[fast]=nums[1]=2=0则交换slow和fast指向的元素,slow自增

fast=2:

由于
nums
[
fast
]
=
nums
[
2
]
=
0
=
0
\text{nums}[\text{fast}]=\text{nums}[2]=0=0
nums[fast]=nums[2]=0=0则什么都不做,进入下一次循环
fast=3:

由于
nums
[
fast
]
=
nums
[
3
]
=
3
≠
0
\text{nums}[\text{fast}]=\text{nums}[3]=3\ne0
nums[fast]=nums[3]=3=0则交换slow和fast指向的元素,slow自增

循环结束,数组是[2, 3, 0, 0],结果正确
1.3.3 数组中没有0
假设数组nums[1, 2, 3]
fast=0:

由于 nums [ fast ] = nums [ 0 ] = 1 ≠ 0 \text{nums}[\text{fast}]=\text{nums}[0]=1\ne0 nums[fast]=nums[0]=1=0则交换slow和fast指向的元素(指向同一个元素,相当于没换),slow自增
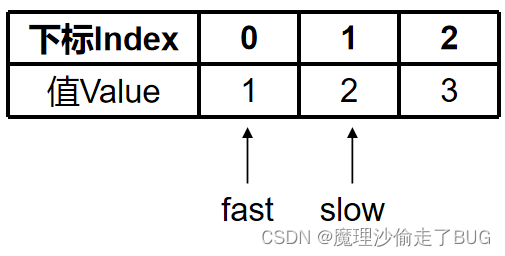
fast=1:

由于
nums
[
fast
]
=
nums
[
1
]
=
2
≠
0
\text{nums}[\text{fast}]=\text{nums}[1]=2\ne0
nums[fast]=nums[1]=2=0则交换slow和fast指向的元素(指向同一个元素,相当于没换),slow自增

fast=2:

由于
nums
[
fast
]
=
nums
[
2
]
=
3
≠
0
\text{nums}[\text{fast}]=\text{nums}[2]=3\ne0
nums[fast]=nums[2]=3=0则交换slow和fast指向的元素(指向同一个元素,相当于没换),slow自增

循环结束,数组是[1,2,3],结果正确
1.4 总结
这个题只要想明白将原来的 O ( n ) O(n) O(n)时间复杂度的移除数组元素的算法的if条件里的逻辑的从右向左覆盖移动改成从左向右交换元素移动就很快写出来,代码再贴一遍(顺利通过):
class Solution {
public:
void moveZeroes(vector<int>& nums) {
//模仿O(n)的删除数组元素的方法删除0
//if条件由nums[fast]!=val改成nums[fast]!=0
//但是这次不是仅仅nums[slow]=nums[fast],而是将它们两个交换
int slow = 0;
int temp = 0;//临时变量存储交换值
for(int fast = 0; fast < nums.size(); fast++)
{
if(nums[fast]!=0)
{
//交换元素位置
temp = nums[slow];
nums[slow] = nums[fast];
nums[fast] = temp;
slow++;
}
}
}
};