一、并查集的原理
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find
set)。
这样讲可能有点抽象,下面我通过一个故事来帮助大家理解这个并查集的现实意义。
这是一个充满打打杀杀的江湖,每个人都混迹在江湖之中,去追寻自己的理想和抱负,时常会因为信仰不同而聚众斗殴,江湖上常常乱作一团,但是也有时也会因为信仰相同,结成好朋友,共同对抗别人,随着时间的增长,不同的团体规模也在不断扩大,大家也在尝试去依附团体生存。于是就形成了不同的帮派。
帮派的形成本身就是为了能够有自己的盟友去帮助合力对抗外人,这个时候就出现了一个问题,我们如何去分辨自己的盟友呢?? 避免打错人呢?? 所以为了解决这个问题,每个帮派都需要有一个掌门人,这样在决斗的时候,双方通过自报家门,就能知道是自己人还是敌人了。
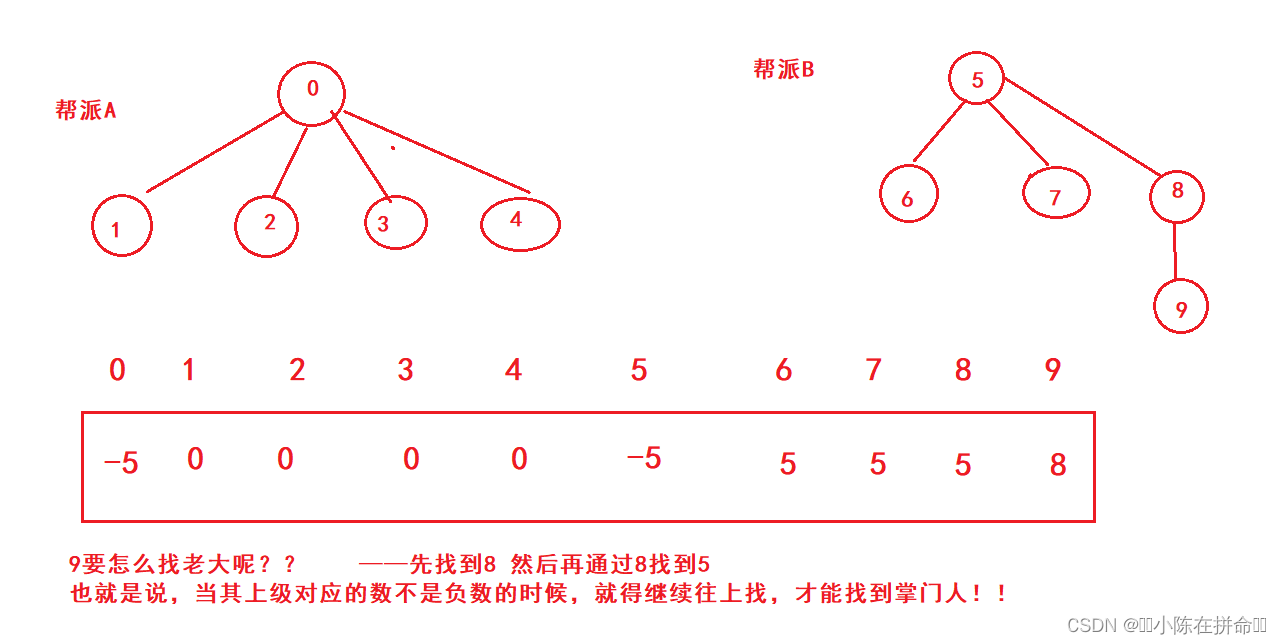
接下来我们来通过并查集模拟形成帮派的过程
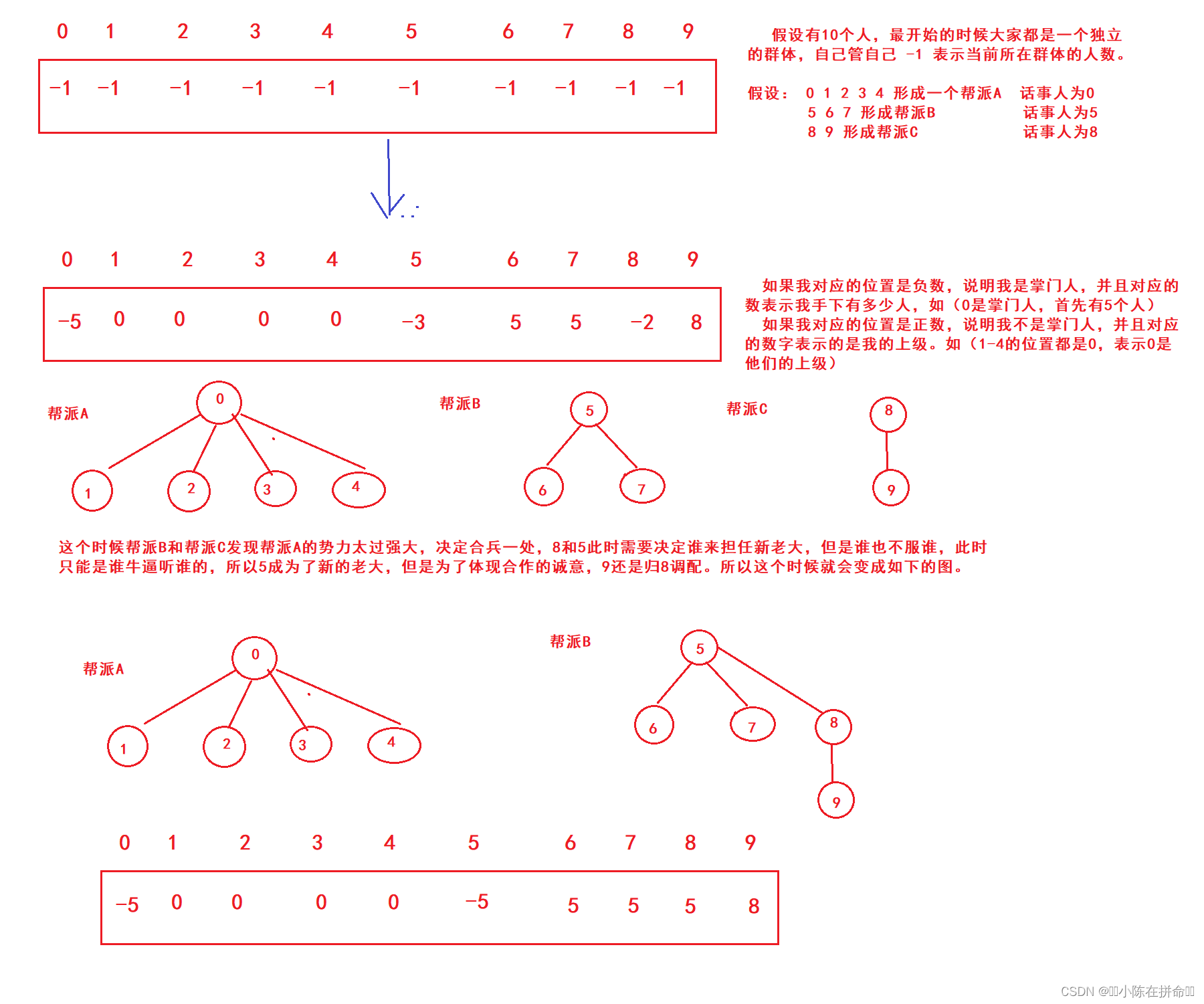
从上图可以看出,并查集其实是一种树形结构,只不过用的是双亲表示法。
通过以上例子可知,并查集一般可以解决一下问题:
1. 查找元素属于哪个集合
沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
3. 将两个集合归并成一个集合
将两个集合中的元素合并
将一个集合名称改成另一个集合的名称
4. 集合的个数
遍历数组,数组中元素为负数的个数即为集合的个数。
二、并查集的模拟实现
我们封装并查集,需要有一个vector<int>类型的成员函数。
2.1 并查集的初始化
UnionFindSet(size_t n)
:_set(n, -1) //初始化成-1 并查集的初始状态
{}
直接调用vector的构造函数。初始化成-1
2.2 寻找某节点的根Findroot
两个高手刚见面,首先就得自报家门,看看自己的老大是不是同一个,这样才能决定是打一架还是吃个饭。因此我们要实现一个Findroot 。
size_t Findroot(size_t x)
{
while (_set[x] >= 0) x = _set[x]; //去找根节点
return x;
}但是这样真的好吗???

我们用递归的方式去修改,不断去修改我们要查找节点的前驱节点,这样在下一次找这个数的时候,必然只需要O(1)的时间复杂度就可以完成了!
int Findroot(int x) //查找结点 x的根结点
{
if (_set[x]< 0) return x; //递归出口:x的上级为 x本身,即 x为根结点
return _set[x] = Findroot(_set[x]); //此代码相当于先找到根结点 rootx,然后_set[x]=rootx
}2.3 合并两个集合union
我们俩要结盟,在结盟之前,我们要先判断我们俩是不是自己人,所以要先找到我们的老大。如果我们的老大是同一个,那么就没有必要再结盟,但是如果我们俩不是同一个老大,这个时候结盟前就需要有一个老大去当另一个老大的小弟。两个谁也不服谁,所以只能比一下谁人多,最后人少听人多的。

所以我们找到老大后,还需要判断老大手下有多少人,谁人少,就将所有人划分到人多的那一边去。
bool Union(int x, int y) //优化思路 大树管小树
{
int root1 = Findroot(x);
int root2 = Findroot(y);
if (root1 == root2) return false;//说明两个在一个集合,所以没有必要去合并
//此时说明可以合并了
if (_set[root1] > _set[root2]) swap(root1, root2); //_set[root1] 表示root1手下有多少人 手下人少投靠手下人多的
_set[root1] += _set[root2];//我把我手下的人包括我自己归属于你
_set[root2] = root1;//你成为我的上级。
return true;
}其实该方式本质上也是为了尽可能地降低整体节点的深度,方便查找可以更快。
2.4 统计并查集中一共有多少个集合
遍历一遍并查集,数一下有多少个掌门人即可
size_t SetCount()//查找一共有几个集合
{
size_t count = 0;
for (auto& e : _set)
if (e < 0) ++count;
return count;
}2.5 并查集的整体代码实现
#include<vector>
#include<iostream>
using namespace std;
class UnionFindSet //利用的是双亲表示法
{
public:
UnionFindSet(size_t n)
:_set(n, -1) //初始化成-1 并查集的初始状态
{}
size_t Findroot(size_t x) //非压缩版本
{
while (_set[x] >= 0) x = _set[x]; //去找根节点
return x;
}
int Findroot(int x) //查找结点 x的根结点 压缩版本
{
if (_set[x]< 0) return x; //递归出口:x的上级为 x本身,即 x为根结点
return _set[x] = Findroot(_set[x]); //此代码相当于先找到根结点 rootx,然后_set[x]=rootx
}
bool Union(int x, int y) //优化思路 大树管小树
{
int root1 = Findroot(x);
int root2 = Findroot(y);
if (root1 == root2) return false;//说明两个在一个集合,所以没有必要去合并
//此时说明可以合并了
if (_set[root1] > _set[root2]) swap(root1, root2); //_set[root1] 表示root1手下有多少人 手下人少投靠手下人多的
_set[root1] += _set[root2];//我把我手下的人包括我自己归属于你
_set[root2] = root1;//你成为我的上级。
return true;
}
size_t SetCount()//查找一共有几个集合
{
size_t count = 0;
for (auto& e : _set)
if (e < 0) ++count;
return count;
}
private:
vector<int> _set;// 并查集
};
三、并查集的相关OJ题
并查集的主要作用是求连通分支数(如果一个图中所有点都存在可达关系(直接或间接相连),则此图的连通分支数为1;如果此图有两大子图各自全部可达,则此图的连通分支数为2……)
3.1 省份数量
. - 力扣(LeetCode)

这边重点使用并查集的思想解决问题
我们会发现这道题的本质其实是,如果两个城市相连就要将他丢进集合里,最后看看并查集里面有几个集合就代表有几个省份。
我们直接用我们之前实现过的并查集来解决问题!!
解法1:手撕并查集
class UnionFindSet //利用的是双亲表示法
{
public:
UnionFindSet(size_t n)
:_set(n, -1) //初始化成-1 并查集的初始状态
{}
int Findroot(int x) //查找结点 x的根结点 优化
{
if (_set[x]< 0) return x; //递归出口:x的上级为 x本身,即 x为根结点
return _set[x] = Findroot(_set[x]); //此代码相当于先找到根结点 rootx,然后_set[x]=rootx
}
bool Union(int x, int y)
{
int root1 = Findroot(x);
int root2 = Findroot(y);
if (root1 == root2) return false;//说明两个在一个集合,所以没有必要去合并
//此时说明可以合并了
if (_set[root1] > _set[root2]) swap(root1, root2); //_set[root1] 表示root1手下有多少人 手下人少投靠手下人多的
_set[root1] += _set[root2];//我把我手下的人包括我自己归属于你
_set[root2] = root1;//你成为我的上级。
return true;
}
size_t SetCount()//查找一共有几个集合
{
size_t count = 0;
for (auto& e : _set)
if (e < 0) ++count;
return count;
}
private:
vector<int> _set;// 并查集
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
UnionFindSet set(isConnected.size());//创建一个并查集
for(int i=0;i<isConnected.size();++i)
for(int j=0;j<isConnected[0].size();++j)
if(isConnected[i][j] == 1) //丢到集合里
set.Union(i,j);
return set.SetCount();//返回集合的个数
}
};如果并查集是库里面的,这样做真的很方便,但是实际上我们要使用的话都得自己封装,如果这仅仅是一道OJ题,显然是没有必要的,因为复用性并不高。所以我们按照并查集的逻辑去解题,但是不要真的去实现
解法2:不手撕并查集,但是按照并查集的逻辑去解决问题。
这边针对这一道题,我们可以直接使用lambda表达式去简化我们的代码
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected)
{
vector<int> ufs(isConnected.size(),-1);
auto Findroot=[&ufs](int x)
{
while(ufs[x]>=0) x=ufs[x];
return x;
};
for(int i=0;i<isConnected.size();++i)
for(int j=0;j<isConnected[0].size();++j)
if(isConnected[i][j] == 1) //丢到集合里
{
int root1 = Findroot(i);
int root2 = Findroot(j);
if(root1 != root2)
{
if (ufs[root1] > ufs[root2]) swap(root1, root2);
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
}
size_t count = 0;
for (auto& e :ufs)
if (e < 0) ++count;
return count;
}
};3.2 等式方程的可满足性
. - 力扣(LeetCode)

解决思路就是第一遍我们先将所有相等的值加到一个集合里,然后第二遍去判断不相等的值是否在一个集合里,如果是的话就是错误的。
class Solution {
public:
bool equationsPossible(vector<string>& equations) {
vector<int> ufs(26,-1);
auto Findroot=[&ufs](int x)
{
while(ufs[x]>=0) x=ufs[x];
return x;
};
for(auto&s:equations)
{
if(s[1]=='=')//必然是相等的
{
int root1=Findroot(s[0]-'a');
int root2=Findroot(s[3]-'a');
if(root1!=root2)
{
if(ufs[root1]>ufs[root2]) swap(root1,root2);
//进行合并
ufs[root1]+=ufs[root2];//吞并另一个老大的人
ufs[root2]=root1;//服从指挥
}
}
}
//第二遍 看看是否不是一个集合的
for(auto&s:equations)
{
if(s[1]=='!')//必然是相等的
{
int root1=Findroot(s[0]-'a');
int root2=Findroot(s[3]-'a');
if(root1==root2) return false;
}
}
return true;
}
};