题目
200:Solitaire
总时间限制: 5000ms 单个测试点时间限制: 1000ms 内存限制: 65536kB
描述
Solitaire is a game played on a chessboard 8x8. The rows and columns of the chessboard are numbered from 1 to 8, from the top to the bottom and from left to right respectively.
There are four identical pieces on the board. In one move it is allowed to:move a piece to an empty neighboring field (up, down, left or right),jump over one neighboring piece to an empty field (up, down, left or right).
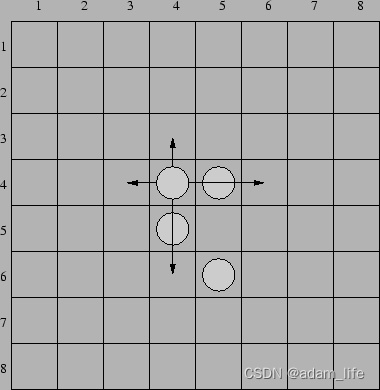
There are 4 moves allowed for each piece in the configuration shown above. As an example let’s consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.
Write a program that:
reads two chessboard configurations from the standard input,verifies whether the second one is reachable from the first one in at most 8 moves,
writes the result to the standard output.
输入
Each of two input lines contains 8 integers a1, a2, …, a8 separated by single spaces and describes one configuration of pieces on the chessboard. Integers a2j-1 and a2j (1 <= j <= 4) describe the position of one piece – the row number and the column number respectively.
输出
The output should contain one word YES if a configuration described in the second input line is reachable from the configuration described in the first input line in at most 8 moves, or one word NO otherwise.
样例输入
4 4 4 5 5 4 6 5
2 4 3 3 3 6 4 6
样例输出
YES
翻译
8*8的棋盘有四个棋子,输入四个棋子的位置和输出的位置,判断在8步内能不能走到。
理解
1.棋盘中四个棋子座位为一个布局作为整体操作,用struct,有四个横坐标,四个纵坐标。
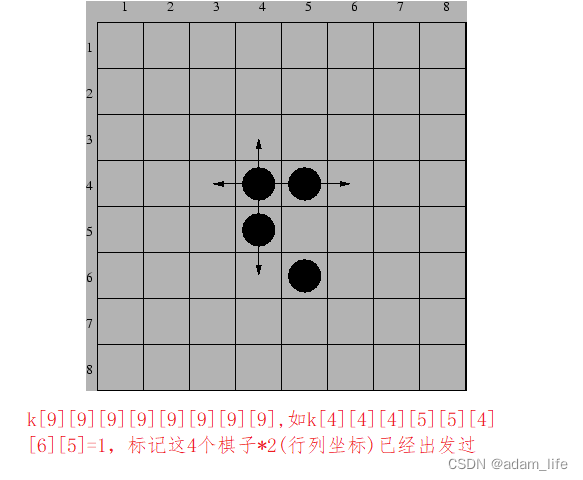
2.四个棋子四个方向独立运行,只要没走过就走,宽搜,枚举到达目标布局。

3.标记棋盘走出哪些布局,4个坐标——8维数组,每两个是一个坐标。如始发布局k[4][4][4][5][5][4][6][5]=1。
4.最终落棋位置用布尔数组goal[9][9]表示,0-8(9个数)的数组,两个维度就是一对坐标。
要判断到终点没,就是四个棋子的位置都是终点标记位置
四个棋子有四个坐标,goal[4][4]=1,goal[4][5]=1,goal[5][4]=1, goal[6][5]=1都是1就说明到达目的地。
5.判断是否出界。
6.要判断是否重叠,如果重叠得还得走一次,再判断出界和重叠
走完后,如果没有出界,不是已走过,没有重叠,
再看是否到终点没
否则就加入队列,
代码
#include <bits/stdc++.h>
using namespace std;
struct cbord{//一张棋盘四个棋子坐标,到达该布局的步数
int x[4],y[4],step;
}s,b;//出发布局,宽搜队首布局
bool k[9][9][9][9][9][9][9][9],//88(1-8)棋盘上4个棋子坐标(42=8)宽搜标记
goal[9][9];//四个目标位置的坐标。
int d[4][2]={{0,-1},{-1,0},{0,1},{1,0}};//左上右下移动
bool reached(cbord c){//判定四个棋子位置是不是目标位置
for(int i=0;i<4;i++)
if(!goal[c.x[i]][c.y[i]])return 0;//有个棋子坐标不是目标位置就错
return 1;
}
bool overlap(cbord c,int x){//两棋子是否重叠了
for(int i=0;i<4;i++)
if(i!=x&&c.x[i]==c.x[x]&&c.y[i]==c.y[x])return 1;//有两个棋子位置重了
return 0;
}
void view(cbord c){
for(int i=0;i<4;i++)
cout<<c.x[i]<<“,”<<c.y[i]<<“\t”;
cout<<“=”<<c.step<<endl;
}
bool bfs(){
queue q;q.push(s);
k[s.x[0]][s.y[0]][s.x[1]][s.y[1]][s.x[2]][s.y[2]][s.x[3]][s.y[3]]=1;//标记四个棋子坐标位置已经到过
int x,y;
while(!q.empty()){//广搜
b=q.front();q.pop();
//view(b);
if(b.step>=8)continue;//取消超过8步的走法
if(reached(b))return 1;//到达目标布局
for(int i=0;i<4;i++){//四个棋子
//s=b;//不在这里,每个方向间无顺序相互独立
for(int j=0;j<4;j++){//四个方向
s=b;//拷贝布局,再改
s.x[i]+=d[j][0],s.y[i]+=d[j][1];//改坐标
if(s.x[i]<1||s.x[i]>8||s.y[i]<1||s.y[i]>8)continue;//出界了不要
if(overlap(s,i)){//重叠了
s.x[i]+=d[j][0],s.y[i]+=d[j][1];//可以跳
if(s.x[i]<1||s.x[i]>8||s.y[i]<1||s.y[i]>8)continue;//出界了不要
if(overlap(s,i))continue;//再重叠就不能要了
}
if(k[s.x[0]][s.y[0]][s.x[1]][s.y[1]][s.x[2]][s.y[2]][s.x[3]][s.y[3]])continue;//已经走过这个布局
k[s.x[0]][s.y[0]][s.x[1]][s.y[1]][s.x[2]][s.y[2]][s.x[3]][s.y[3]]=1;//标记
s.step++;//多一步
if(reached(s))return 1;//到达目标布局
q.push(s);//放进队列再宽搜
}
}
}
return 0;
}
int main(){
//freopen(“data.cpp”,“r”,stdin);
for(int i=0;i<4;i++)cin>>s.x[i]>>s.y[i];
int x,y;
for(int i=0;i<4;i++){
cin>>x>>y;goal[x][y]=1;//该位置是其中一个坐标。共有四个棋子位置
}
if(bfs())cout<<“YES”;
else cout<<“NO”;
return 0;
}
小结
宽搜就跟枚举一样,全试。
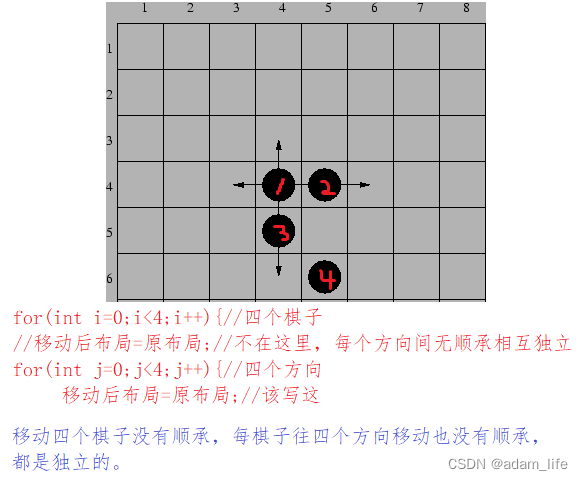
四个棋子四个方向没有先后顺序,相互独立是关键。
for(int i=0;i<4;i++){//四个棋子
//s=b;//不在这里,每个方向间无顺序相互独立
for(int j=0;j<4;j++){//四个方向
s=b;//拷贝布局,再改
s.x[i]+=d[j][0],s.y[i]+=d[j][1];//改坐标