目录

022：求最小公倍数

023：数组中的最长连续子序列

024：字母收集

---

022：求最小公倍数

求最小公倍数_牛客题霸_牛客网 (nowcoder.com)

 题目：

题解：

 求最小公倍数公式：lcm(a,b)=a*b/gcd(a,b)，gcd(a,b)为a,b之间的最小公因数，递归求最小公因数。

#include <iostream>
using namespace std;

//求最小公因数
int gcd(int a,int b)
{
    if(b==0) return a;
    return gcd(b,a%b);
}
int main() 
{
    int A,B;
    cin>>A>>B;

    cout<<A*B/gcd(A,B)<<endl;

}

023：数组中的最长连续子序列

数组中的最长连续子序列_牛客题霸_牛客网 (nowcoder.com)

 1.哈希集合的快速查找

class Solution {
public:

    int MLS(vector<int>& arr) 
    {
        int ret=0;
        unordered_set<int> hashSet;
        int i=arr.size();
        for(auto t:arr)
        {
            hashSet.insert(t);
        }
        for(auto t:arr)
        {
            if(hashSet.count(t-1)) continue;
            int len=1;
            while(hashSet.count(++t)) len++;
            ret=max(ret,len);
        }
        return ret;
    }
};

024：字母收集

字母收集_牛客题霸_牛客网 (nowcoder.com)

 题目：

题解：

动态规划：创建dp表保存到{i,j}位置的最大分数，由于只能向下和向右，最终会到{m,n}，最后结果也为dp[m][n]。

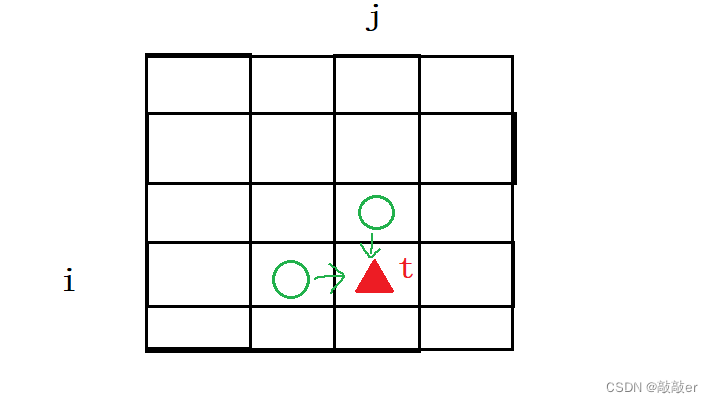
#include <iostream>
using namespace std;
const int N=510;
char g[N][N];
int dp[N][N];
int m,n;
int main()
{
    cin>>m>>n;
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=n;j++)
        {
            cin>>g[i][j];
        }
    }


    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=n;j++)
        {
            int t=0;
            if(g[i][j]=='l') t=4;
            else if(g[i][j]=='o') t=3;
            else if(g[i][j]=='v') t=2;
            else if(g[i][j]=='e') t=1;

            dp[i][j]=max(dp[i-1][j], dp[i][j-1])+t;
        }
    }
    cout<<dp[m][n]<<endl;

    return 0;
}