Union-Find连通性检测之quick-union
理论基础
在图论和计算机科学中,Union-Find 或并查集是一种用于处理一组元素分成的多个不相交集合(即连通分量)的情况,并能快速回答这组元素中任意两个元素是否在同一集合中的问题。Union-Find 特别适用于连通性问题,例如网络连接问题或确定图的连通分量。
Union-Find 的基本操作
Union-Find 数据结构支持两种基本操作:
- Union(合并): 将两个元素所在的集合合并成一个集合。
- Find(查找): 确定某个元素属于哪个集合,这通常涉及找到该集合的“代表元素”或“根元素”。
Union-Find 的结构
Union-Find 通常使用一个整数数组来表示,其中每个元素的值指向它的父节点,这样形成了一种树形结构。集合的“根元素”是其自己的父节点。
Union-Find 的优化技术
为了提高效率,Union-Find 实现中常用两种技术:
- 路径压缩(Path Compression): 在执行“查找”操作时,使路径上的每个节点都直接连接到根节点,从而压缩查找路径,减少后续操作的时间。
- 按秩合并(Union by Rank): 在执行“合并”操作时,总是将较小的树连接到较大的树的根节点上。这里的“秩”可以是树的深度或者树的大小。
应用示例
Union-Find 算法常用于处理动态连通性问题,如网络中的连接/断开问题或者图中连通分量的确定。例如,Kruskal 的最小生成树算法就使用 Union-Find 来选择边,以确保不形成环路。
总结
Union-Find 是解决连通性问题的一种非常高效的数据结构。它能够快速合并集合并快速判断元素之间的连通性。通过路径压缩和按秩合并的优化,Union-Find 在实际应用中可以接近常数时间完成操作。因此,它在算法竞赛、网络连接和社交网络分析等领域有广泛的应用。
数据结构
private int[] id // 分量id(以触点作为索引)
private int count // 分量数量
实验数据和算法流程
本实验使用tinyUF.txt作为实验数据,数据内容如下,一共定义了10对连通性关系
10
4 3
3 8
6 5
9 4
2 1
8 9
5 0
7 2
6 1
1 0
6 7
实验的目的是检测数据中共有多少个连通分量,并打印每个元素所属的连通分量编号
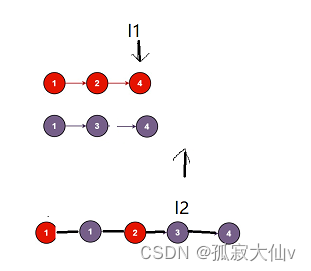
下图展示了处理5和9连通性的一个瞬间
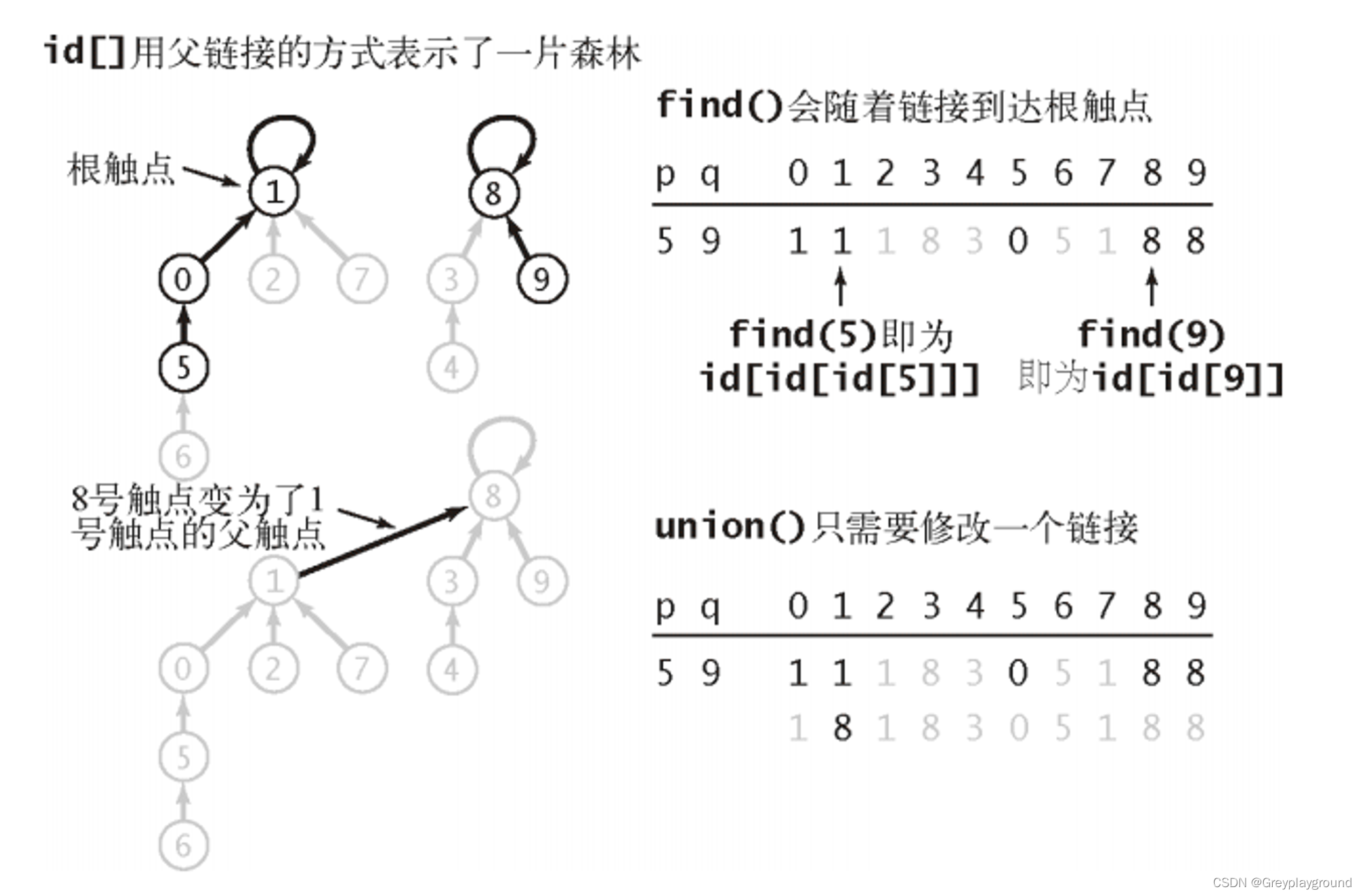
完整流程如下

代码实现
原则是小树挂在大树下,如果一棵高度为1,但是有100个节点的树,要把高度为2的三节点小树挂在这课大树上
可以想象如果反过来,大树挂在小树下,大树的100个节点都将变成高度为3的树枝,这样的话查询的整体成本就太高了
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.StdIn;
public class myQuickUnion {
private int[] id;
private int count;
private int finds;
private int[] size;
public myQuickUnion(int N) { // 初始化分量id数组
count = N;
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
size = new int[N];
for (int i = 0; i < N; i++) size[i] = 1;
}
public boolean connected(int p, int q)
{return find(p) == find(q);}
public int count()
{ return count;}
private int find(int p){
while(p != id[p]){
p = id[p];
finds ++;
}
return p;
}
public void union(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot==qRoot) return;
if(size[pRoot]<size[qRoot])
{id[pRoot]=qRoot;
size[qRoot]+=size[pRoot];}
else
{id[qRoot]=pRoot;
size[pRoot]+=size[qRoot];}
//id[pRoot] = qRoot;
//此处注释掉的是随机将两棵树的根连接的表达式
//根据实测,加权时总的find次数为2000左右,普通union为2万次左右
count --;
}
public static void main(String[] args){
int N = StdIn.readInt();
myQuickUnion qu = new myQuickUnion(N);
while(!StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if(qu.connected(p,q)) continue;
qu.union(p,q);
}
StdOut.println("components: "+qu.count);
for(int i=0;i<N;i++){
StdOut.println(i+":"+qu.id[i]);
}
StdOut.println("find counts: "+qu.finds);
}
}
代码详解
这段代码是一个实现了“加权快速合并”(Weighted Quick Union)的并查集算法的Java类 myQuickUnion。该算法用于处理大量元素的动态连通性问题,提高了普通快速合并(Quick Union)算法的效率。以下是对这段代码的详细解释:
类定义和变量
public class myQuickUnion {
private int[] id; // id数组,用于保存每个节点的父节点
private int count; // 连通分量的数量
private int finds; // 进行find操作的次数统计
private int[] size; // 每个根节点相应的分量大小
id数组中,每个位置保存了该位置元素的父节点索引。count记录当前图中连通分量的数量。finds用于记录执行find操作的次数,有助于分析算法性能。size数组用于保存以每个节点为根的树的大小。
构造函数
public myQuickUnion(int N) {
count = N;
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
size = new int[N];
for (int i = 0; i < N; i++) size[i] = 1;
}
构造函数初始化了 id 数组和 size 数组。id 数组的每个元素初始指向自身,表示每个元素都是自己的根节点。size 数组中的每个元素初始为 1,表示每个根节点的树大小为 1。
方法实现
connected
public boolean connected(int p, int q) {
return find(p) == find(q);
}
检查两个元素是否连通,即它们是否有相同的根。
find
private int find(int p) {
while (p != id[p]) {
p = id[p];
finds++;
}
return p;
}
找到元素 p 的根节点。这里使用了路径压缩的一种简单形式,在找根的过程中顺便统计操作次数。
union
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) return;
if (size[pRoot] < size[qRoot]) {
id[pRoot] = qRoot;
size[qRoot] += size[pRoot];
} else {
id[qRoot] = pRoot;
size[pRoot] += size[qRoot];
}
count--;
}
合并两个元素所在的树。如果一个树的大小小于另一个,小的树的根节点将指向大的树的根节点,并更新树的大小。这种“按大小加权”的策略有助于减少树的高度,从而提高后续操作的效率。
主函数
public static void main(String[] args) {
int N = StdIn.readInt();
myQuickUnion qu = new myQuickUnion(N);
while (!StdIn.isEmpty()) {
int p = StdIn.readInt();
int q = StdIn.readInt();
if (qu.connected(p, q)) continue;
qu.union(p, q);
}
StdOut.println("components: " + qu.count);
for (int i = 0; i < N; i++) {
StdOut.println(i + ":" + qu.id[i]);
}
StdOut.println("find counts: " + qu.finds);
}
在主函数中,从标准输入读取元素数量和成对的整数。每对整数代表一次尝试连接的操作。如果两个元素已经连通,则忽略;否则,进行合并操作。最终,输出连通分量的数量、每个元素的最终根,以及进行 find 操作的总次数。
实验
代码编译
$ javac myQuickUnion.java
代码运行
该算法处理tinyUF.txt时由于使用了加权方法,优先将小树挂在大树下,这样可以极大减少find操作的次数,提高了性能,在打印中可以看到find counts的值为13,即一共执行了13次find,
$ java myQuickUnion < ..\data\tinyUF.txt
components: 2
0:6
1:2
2:6
3:4
4:4
5:6
6:6
7:2
8:4
9:4
find counts: 13
如果将权重处理注释掉,使用普通quick-union方法,find counts数值会变为16,影响性能
如果导入mediumUF.txt或者largeUF.txt数据,这个差距将更加悬殊
java myQuickUnion < ..\data\tinyUF.txt
components: 2
0:1
1:1
2:1
3:8
4:3
5:0
6:5
7:1
8:8
9:8
find counts: 16
参考资料
算法(第四版) 人民邮电出版社