C++中布隆过滤器

news2024/11/24 18:37:38

🐶博主主页：@ᰔᩚ. 一怀明月ꦿ

❤️‍🔥专栏系列：线性代数，C初学者入门训练，题解C，C的使用文章，「初学」C++，linux

🔥座右铭：“不要等到什么都没有了，才下定决心去做”

🚀🚀🚀大家觉不错的话，就恳求大家点点关注，点点小爱心，指点指点🚀🚀🚀

布隆过滤器

布隆过滤器的原理

添加元素

具体使用场景

BKDRHash

APHash

DJBHash

哈希分割

布隆过滤器

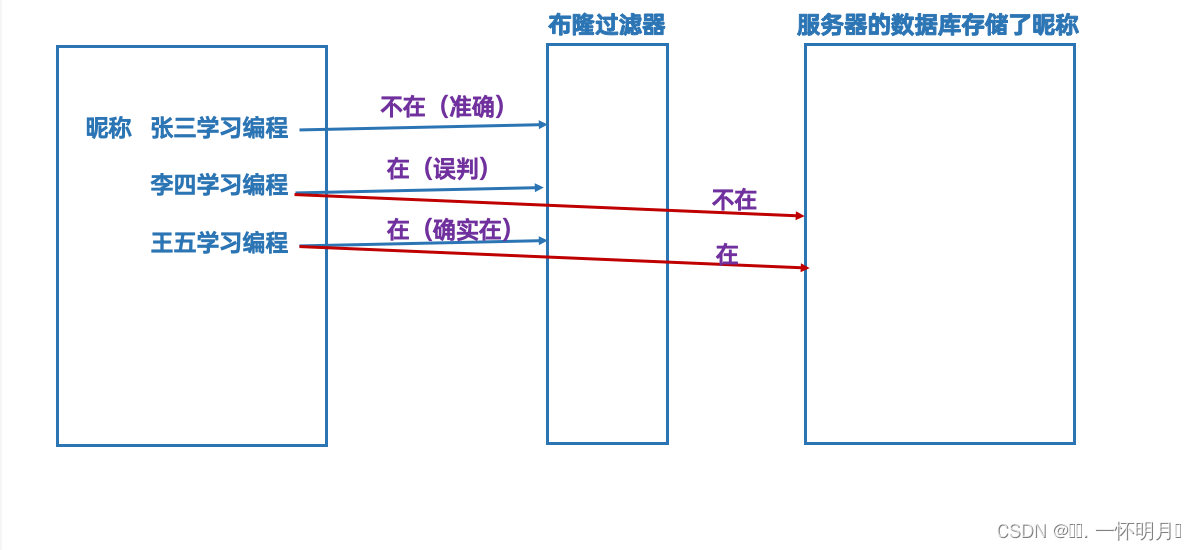
布隆过滤器（Bloom Filter）是一种数据结构，用于快速检查一个元素是否属于一个集合中。它通过使用一系列哈希函数和位数组来实现。当一个元素被添加到布隆过滤器时，将对其进行多次哈希，并将相应的位数组位置设置为1。当检查一个元素是否在集合中时，布隆过滤器会对该元素进行相同的哈希，并检查对应的位数组位置是否都为1，若其中有一个位置不为1，则可以确定该元素不在集合中；若都为1，则该元素可能在集合中（存在一定的误判率）。

布隆过滤器的主要优点是空间效率和查询速度高，因为它不需要存储实际的元素内容，只需要存储一系列位的数组。但是，布隆过滤器也有一定的缺点，主要是存在误判率（可能会判断一个不在集合中的元素为在集合中）以及不支持元素的删除操作。

常见的应用场景包括网络爬虫中的URL去重、数据库查询优化中的缓存、拼写检查等。

布隆过滤器的原理

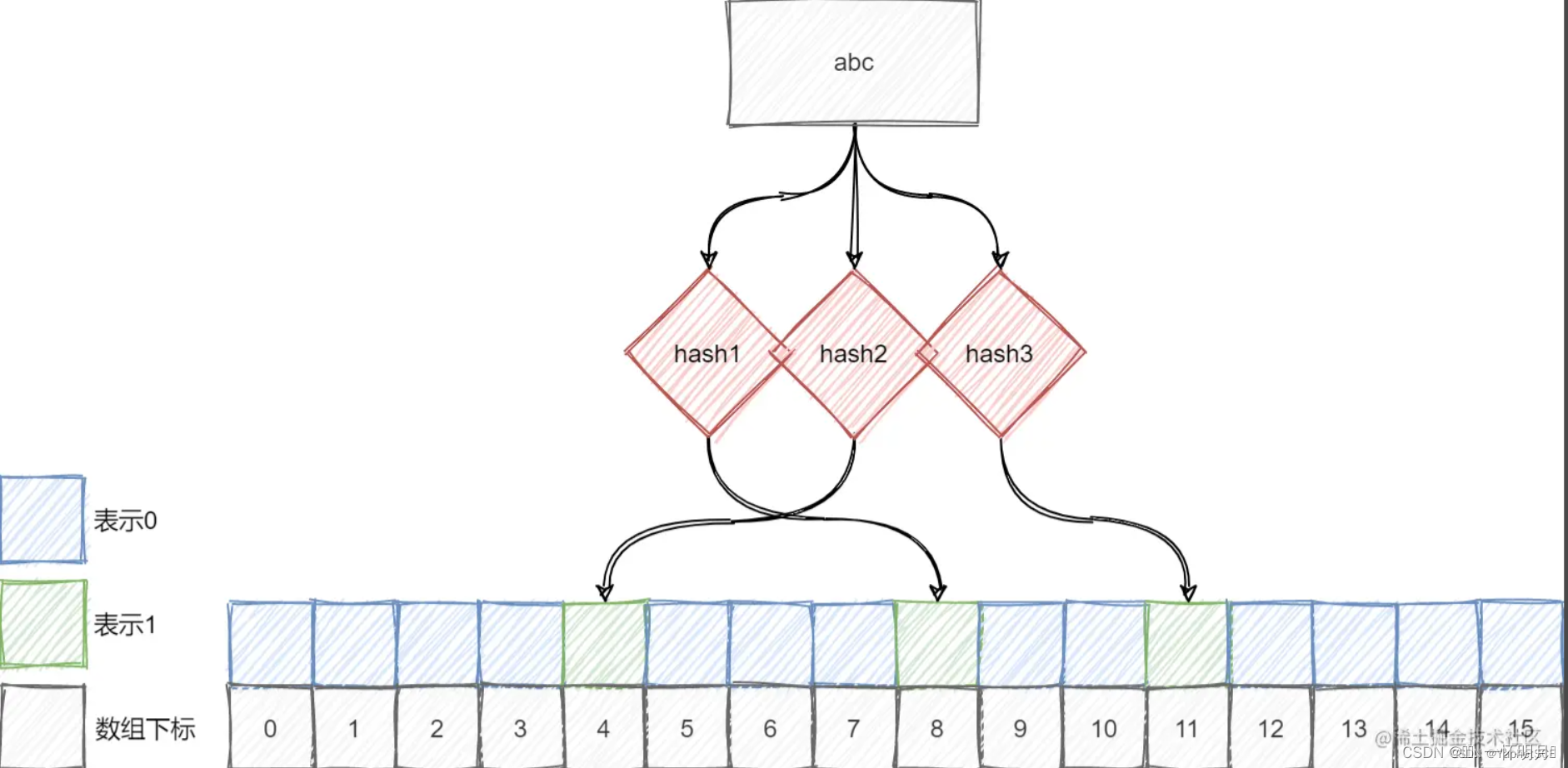
一个值映射多个比特位，还是可能存在冲突，映射多个位，降低误判的概率，布隆过滤器的数据结构是一个位向量，也就是一个由0、1所组成的bit数组

添加元素

每个元素添加进布隆过滤器前，都会经过多个不同的哈希函数，计算出不同的哈希值，然后映射到位向量上，也就是对应的位"置1"

对元素进行多个不同的哈希运算，得到多个位下标，判断所有映射位置是否都为1，若是，则元素可能存在，否则一定不存在

注意：由于不同的值通过哈希函数之后可能会映射到相同的位置，因此如果一个不存在的元素对应的位都被其他元素所设置1，则查询时就会误判

具体使用场景

如果存在一个数据库，存储的都是都是用的昵称，我们用注册时，需要注册昵称，但是昵称不能和数据库存储的昵称重复，所以就需要在用户注册昵称时，去查询数据库是否存在该昵称。但是传统查询效率太低了，使用哈希表的方式查询的话，可以将字符串转为整形，进行映射但是会面临一个问题，整形开辟的最大空间是42亿多（因为最大的无符号整数是2^32或2^64）,但是字符串接近无限大，例如，一个10长度的单词，就有19275223968000之多所以用整数完全存储不了字符串，而且单纯的哈希表，可能导致多个字符串对应一个整数。因此布隆过滤器非常有必要，布隆过滤器底层思想还是哈希，和传统的哈希表不一样。布隆过滤器使用了位图，用多个位置表示一个字符串，这里我们需要将字符串转成的方法。

BKDRHash
unsigned int BKDRHash(const std::string& key) {
    unsigned int seed = 131; // 31 131 1313 13131 131313 etc..
    unsigned int hash = 0;
    for (char c : key) {
        hash = hash * seed + c;
    }
    return hash;
}
稳定性：较为稳定，具有良好的分布性。

APHash
unsigned int APHash(const std::string& key) {
    unsigned int hash = 0;
    for (char c : key) {
        hash ^= ((hash << 7) ^ c ^ (hash >> 3));
    }
    return hash;
}
稳定性：稳定，适用于大多数情况。

DJBHash
unsigned int DJBHash(const std::string& key) {
    unsigned int hash = 5381;
    for (char c : key) {
        hash = ((hash << 5) + hash) + c;
    }
    return hash;
}
稳定性：非常稳定，被广泛使用。

一般使用三个转换方法效率就很高了（就是用三个比特位对应一个字符串）。使用布隆过滤器，我们就可以准觉的判断一个昵称是否在数据库已经存在，这样的时间效率O(1)

但是，布隆过滤器也有一定的缺点，主要是存在误判率（可能会判断一个不在集合中的元素为在集合中）以及不支持元素的删除操作。

哈希分割

1. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法

2. 如何扩展BloomFilter使得它支持删除元素的操作

假设平均一个query（查询字符）50byte

1G约等于10byte

100亿query 5000byte 约等于500G

哈希表/红黑树空间严重不足

1.

第一步：将两个文件分别哈希分割到多个小文件中

读取每个query，计算i=Hash(query)%500，i是几，query就进入到Ai小文件

读取每个query，计算i=Hash(query)%500，i是几，query就进入到Bi小文件

2.Ai和Bi分别插入到setA和setB，快速找交集

有一个问题，就是分割文件也挺大怎么办，例如：10G文件

情况有两种：

1）这个文件中有很多重复query

2））这个文件中有不同的query

解决方案：

其实很简单，Ai和Bi分别直接插入到setA和setB，如果是情况1），query大量重复，后面插入会失败（因为set不允许重复值插入），情况二，不断插入set以后，内存不足就会抛出异常，就需要换一个哈希函数，进行二次切分，再找交集

给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？与上题条件相同，

如何找到top K的IP？

1.i=Hash(ip)%100

这个ip就进入同一个文件，相同的ip一定会进同一个文件，不同的ip也会进同一个文件，但是同一个ip不会进不同的文件

2.用map依次统计每个文件ip次数，然后比较每个文件最多的ip