参考:
【课程笔记】南大软件分析课程8——指针分析-上下文敏感(课时11/12) - 简书
-------------------------------------------------------------------------------------------------------------
1. 上下文不敏感的问题
说明:上下文敏感分析是对指针分析的准确性提升最有效的技术。
(1)问题

问题:上下文不敏感时,分析常量传播这个问题,由于没有明确调用id()的上下文,会把不同的调用混合在一起,对id函数内的变量n只有一种表示(没有对局部变量进行区分),导致n指向的对象集合增大,将i识别为非常量NAC。实际上,x.get()的值只来自于One()对象,i应该是常量1。
解决:根据调用的上下文(主要有3种:如根据调用点所在的行数——call-site sensitivity)来区分局部变量。
(2)上下文敏感分析
概念:
-
call-site sensitivity (call-string):根据调用点位置的不同来区分上下文。
-
Cloning-Based Context Sensitivity:每种上下文对应一个节点(克隆一次数据)。克隆多少数据,后面会讨论。

Context-Sensitive Heap:面向对象程序(如Java)会频繁修改堆对象,所以不仅要给变量加上下文,也要给堆抽象加上下文,称为heap context。
堆抽象上下文示例:
堆抽象上下文不敏感:如果不区分8 X x = new X();调用的堆抽象的上下文,导致只有1个o8,把两个上下文调用产生的o8.f指向集合都合并了,得出了o8.f的多余指向的结果。
堆抽象上下文敏感:用不同的调用者来区分堆抽象,如3:o8、4:o8是不同的堆抽象。所以说,既要根据上下文的不同来区分局部变量,也要区分堆抽象,例如:3:p是给变量加上下文,3:o8是给堆抽象加上下文。
2. Context Sensitive Pointer Analysis:Rules
标记:根据调用者的行数来区分不同上下文。
C—上下文(暂时用调用点的行数表示),O—对象,F—对象中的域。

规则:
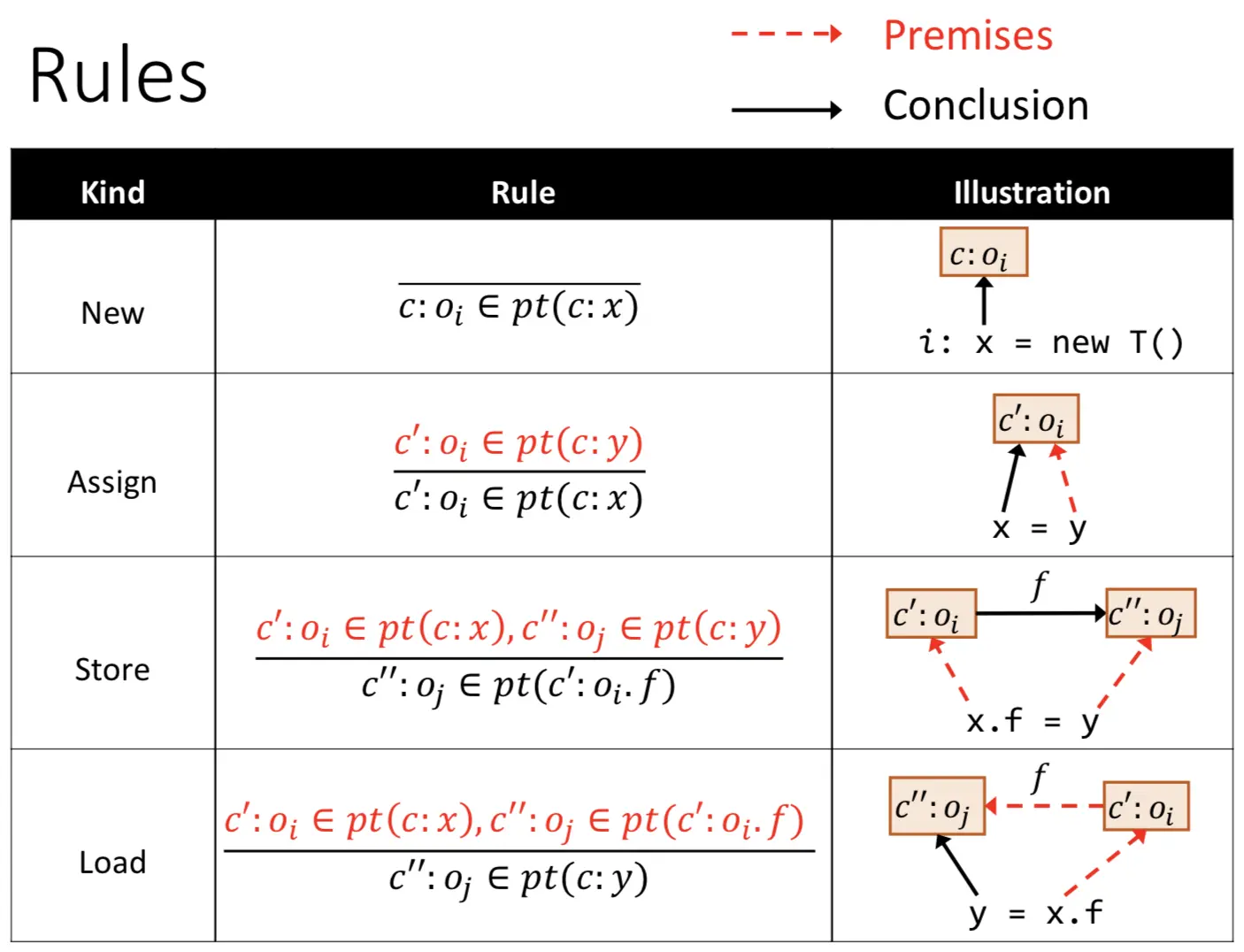
call指令规则:
- 上下文对于Dispatch(oi, k)(找目标函数)没有影响,根据oi指向和函数签名k找到目标函数。
- select(c, l, c':oi, m)根据调用时的信息来给调用目标函数选择上下文(c是调用者的上下文,l是调用者的行号,c':oi是x对象在c'上下文的指向集合,m是目标函数)。
- ct表示目标函数的上下文(后面会讲如何Select选择上下文)。
- 传递this变量:ct:mthis
- 传递参数:ct:mpj
- 传递返回值:ct:mret

3. Context Sensitive Pointer Analysis:Algorithms
区别:和过程间指针分析相比,仍然分为两个过程,分别是构造PFG和根据PFG传递指向信息。主要区别是添加了上下文。

符号:
-
S:可达语句的集合
-
Sm:函数m中的语句
-
RM:可达函数的集合
-
CG:调用图的边
4. Context Sensitivity Variants(上下文的选取)
上下文的选取主要采用3类:
- Call-Site Sensitivity
- Object Sensitivity
- Type Sensitivity
- ...
说明:Select(c,l,c':oi,m),c——调用者上下文,l——调用行,c':oi——接收对象(含堆的上下文信息),m——调用函数。
(1)Call-Site Sensitivity
原理:又称为k-call-site sensitivity / k-CFA,上下文信息为调用行号。1991年Olin Shivers提出。
Select(c,l,c':oi,m) = (l',...,l'', l)
问题:如何限制上下文长度?
解决:k-limiting Context Abstraction。只取最后k个上下文,通常取k<=3。例如,函数的上下文通常取2,堆上下文通常取1。
示例:采用1-Call-Site。
interface Number { int get(); }
class One implements Number { public int get() { return 1; }}
class Two implements Number { public int get() { return 2; }}
1 class C {
2 static void main() {
3 C c = new C();
4 c.m();
5 }
6
7 Number id(Number n) {
8 return n;
9 }
10 void m() {
11 Number n1,n2,x,y;
12 n1 = new One();
13 n2 = new Two();
14 x = this.id(n1);
15 y = this.id(n2);
16 x.get();
17 }
18 }
上下文不敏感vs上下文敏感(1-Call-Site):
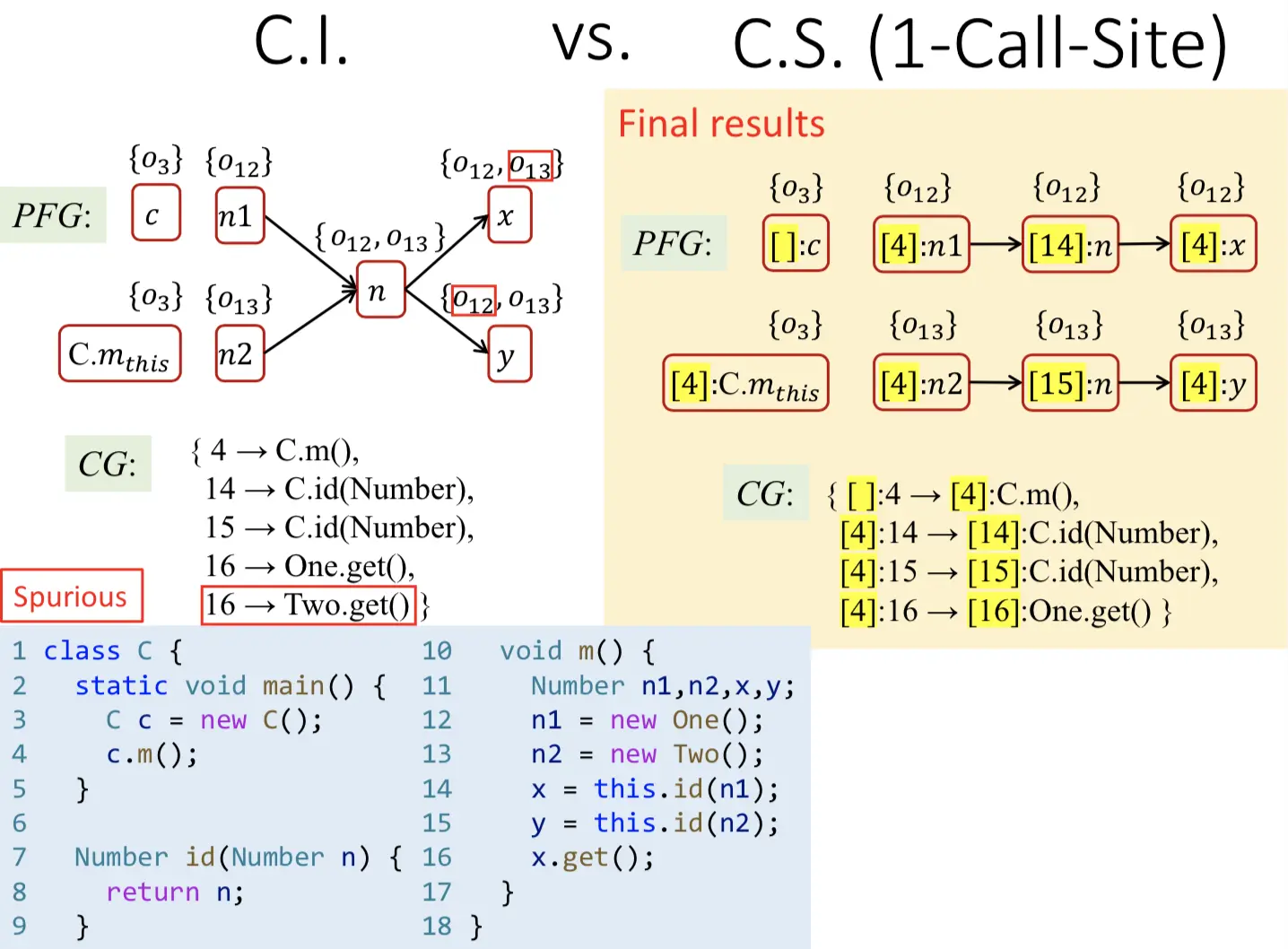
(2)Object Sensitivity
原理:针对面向对象语言,用receiver object来表示上下文。对比1层的调用点敏感和对象敏感,时间和准确性上对象敏感显然更优,这是由面向对象语言的特点所确定的。
Select(c,l,c':oi,m) = [oj, ... , ok, oi] (c' = [oj, ... , ok])
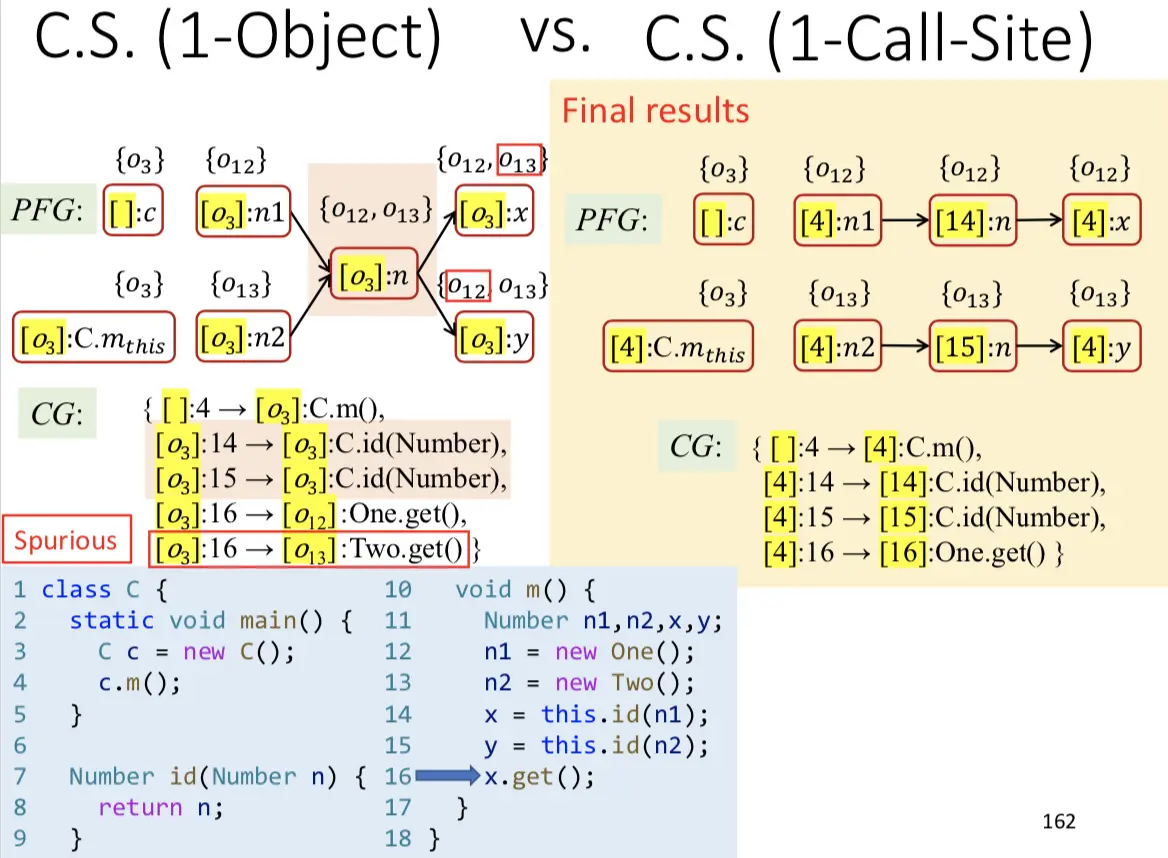
示例:选取1-object,最终pt(x)=o3。

对比:对比1-Call-Site和1-object上下文,在这个示例中1-object明显更准确。原因是面向对象语言的特性,多态性产生很多继承链,一层一层调用子对象,其中最关键的是receiver object,receiver object决定了调用者的根源。本例有若采用2-Call-Site就不会出错。
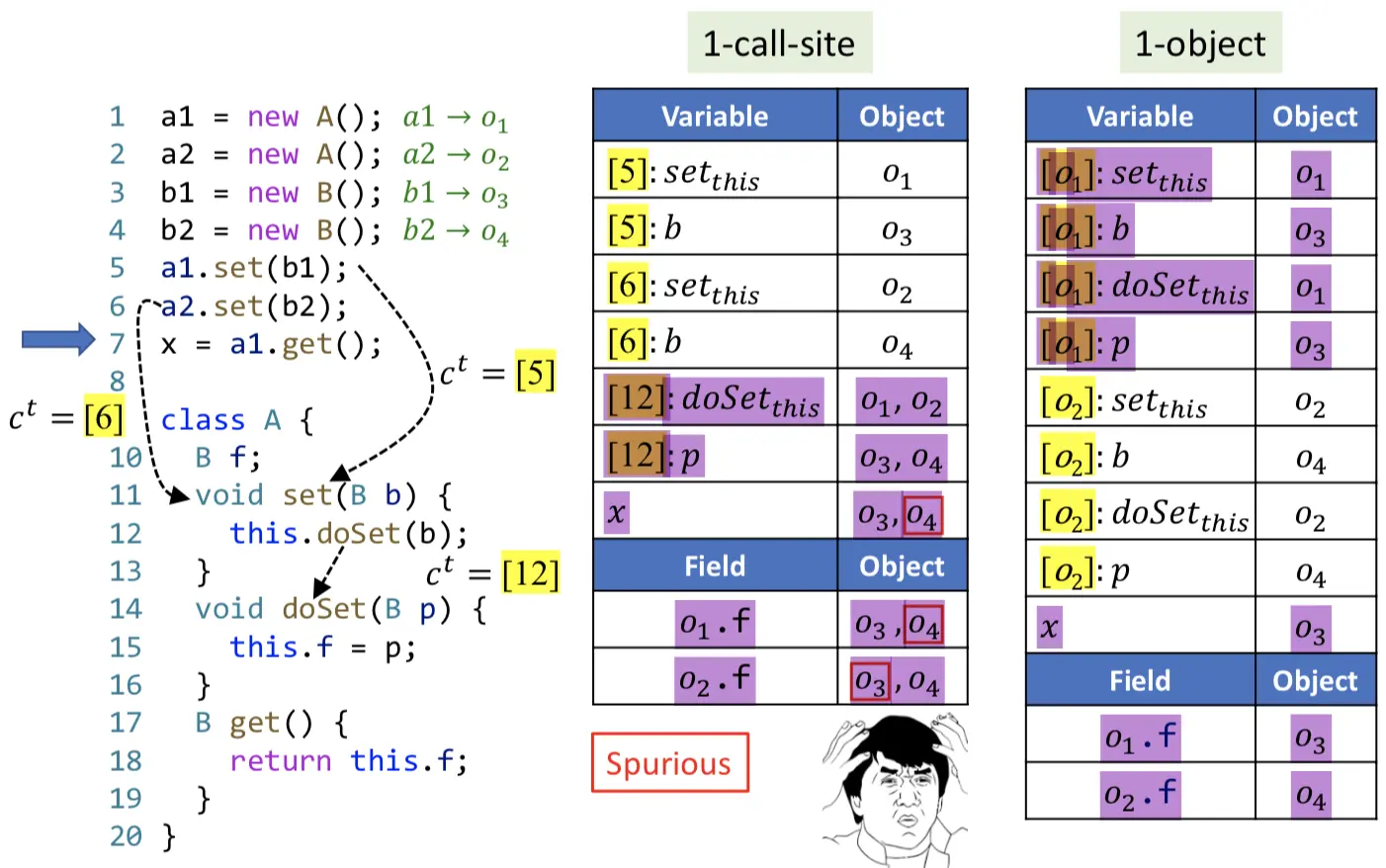
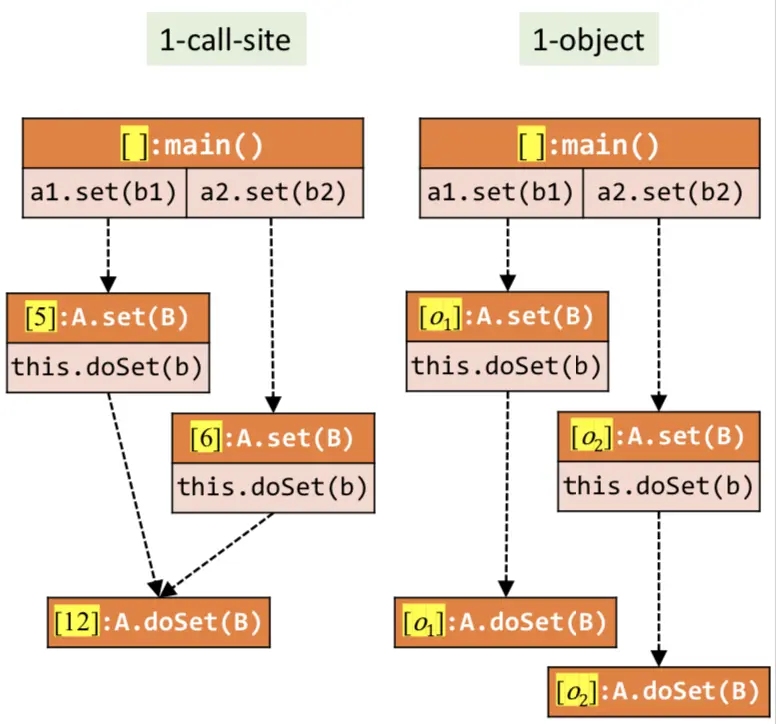
示例2:在本示例中,1-Call-Site明显更准确。因为同一个receiver object用不同参数多次调用了子函数,导致局部变量无法区分。
结论:所以理论上,对象敏感与call site敏感的准确度无法比较。但是对于面向对象语言,对象敏感的准确度要优于call site敏感。
(3)Type Sensitivity
原理:牺牲精度,提高速度。基于创建点所在的类型,是基于对象敏感粗粒度的抽象,精度较低。
Select(c,l,c':oi,m) = [𝑡′,...,𝑡′′,InType(𝑜𝑖)] 其中𝑐′ = [𝑡′, ... , 𝑡′′]

(4)总体对比
精度:object > type > call-site
效率:type > object > call-site
本课老师提出选择上下文的方法,对代码的特点有针对性的选择上下文方法,见A Principled Approach to Selective Context Sensitivity for Pointer Analysis。
课后问题
问题1:流敏感和上下文敏感对变量/堆抽象的表示有什么区别?
- 上下文敏感:某个变量在不同上下文的指向。
- 流敏感:比如说程序运行到第4行,在这个位置变量的指向是什么,第20行又指向哪些,以控制流的位置来作为区分度。
问题2:循环展开还是不展开?
本课程分析的是流不敏感,所以不会展开循环。Java分析不需要流敏感,开销太大了,效果不明显。