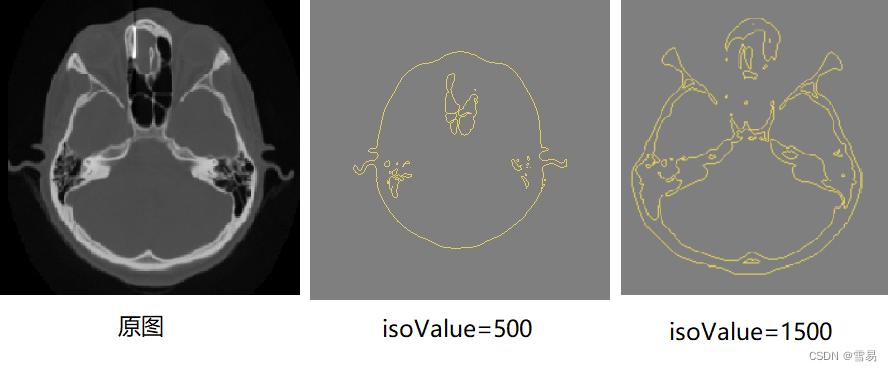
力扣对应链接:LCR 126. 斐波那契数 - 力扣(LeetCode)
牛客对应链接:斐波那契数列_牛客题霸_牛客网 (nowcoder.com)
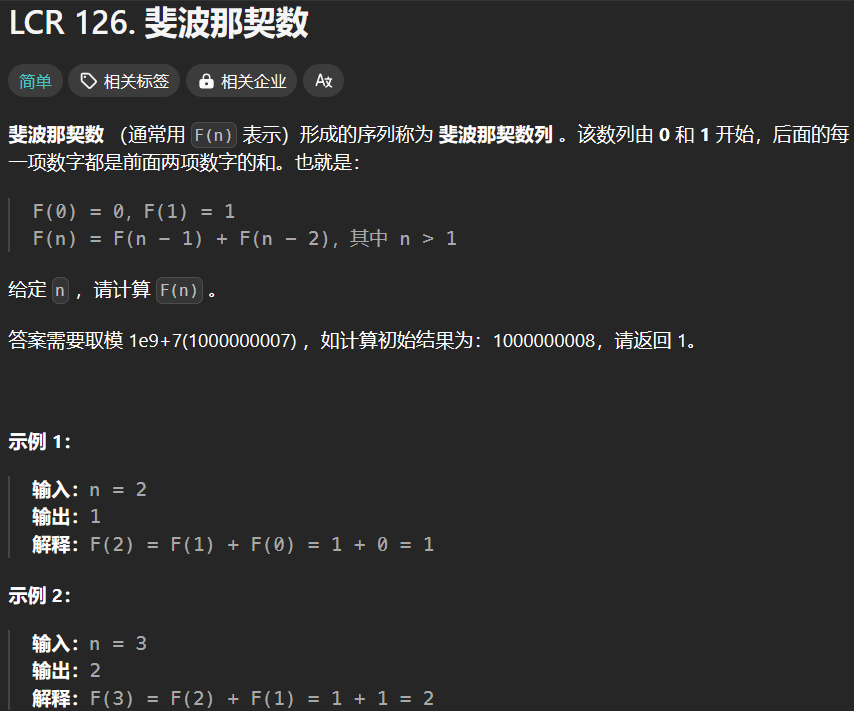
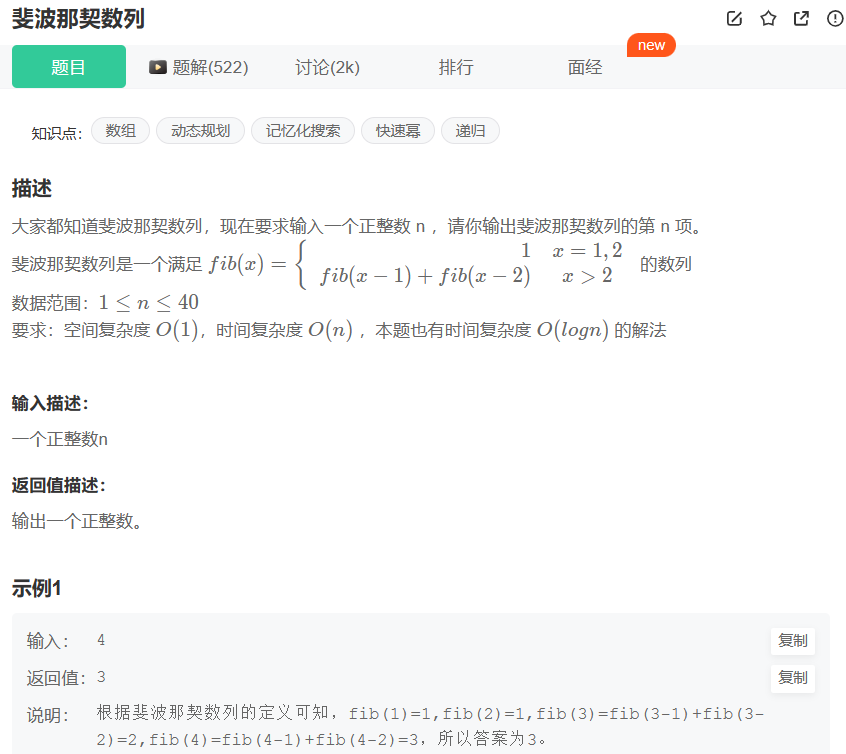
核心考点:空间复杂度,fib 理解,剪枝重复计算。
一、《剑指Offer》内容







二、分析问题
斐波那契数列是:0 1 1 2 3 5 8 13 21 ...
解题方式很多,有递归方式,也有动归(迭代)方式,但是都是最简单的方式。
三、代码
1、方法一(迭代)
//力扣AC代码
class Solution {
private:
int MOD=1e9+7;
public:
int fib(int n) {
if(n==0) return 0;
int first=1;
int second=1;
int third=1;
while(n>2)
{
third=(first+second)%MOD;
first=second;
second=third;
n--;
}
return third;
}
};
//牛客AC代码
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param n int整型
* @return int整型
*/
int Fibonacci(int n) {
int first=1;
int second=1;
int third=1;
while(n>2)
{
third=first+second;
first=second;
second=third;
n--;
}
return third;
}
};2、方法二(递归 + 剪枝)
直接用最简单的方式因为代码空间复杂度过高,过不了 OJ,所以可以采用 map 进行 “剪枝”。
//力扣AC代码
class Solution {
private:
int MOD=1e9+7;
unordered_map<int, int> filter;
public:
int fib(int n) {
if(n==0 || n==1) return n;
if(n==2) return 1;
int ppre=0;
if(filter.find(n-2)==filter.end())
{
ppre=fib(n-2);
filter.insert({n-2, ppre});
}
else
ppre=filter[n-2];
int pre=0;
if(filter.find(n-1)==filter.end())
{
pre=fib(n-1);
filter.insert({n-1, pre});
}
else
pre=filter[n-1];
return (ppre+pre)%MOD;
}
};
//牛客AC代码
#include <unordered_map>
class Solution {
private:
unordered_map<int, int> filter;
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param n int整型
* @return int整型
*/
int Fibonacci(int n) {
if(n==0 || n==1) return n;
if(n==2) return 1;
int ppre=0;
if(filter.find(n-2)==filter.end())
{
ppre=Fibonacci(n-2);
filter.insert({n-2, ppre});
}
else ppre=filter[n-2];
int pre=0;
if(filter.find(n-1)==filter.end())
{
pre=Fibonacci(n-1);
filter.insert({n-1, pre});
}
else pre=filter[n-1];
return ppre+pre;
}
};四、相关错题
【错题集-编程题】Fibonacci数列(Fib 数列)-CSDN博客
五、扩展
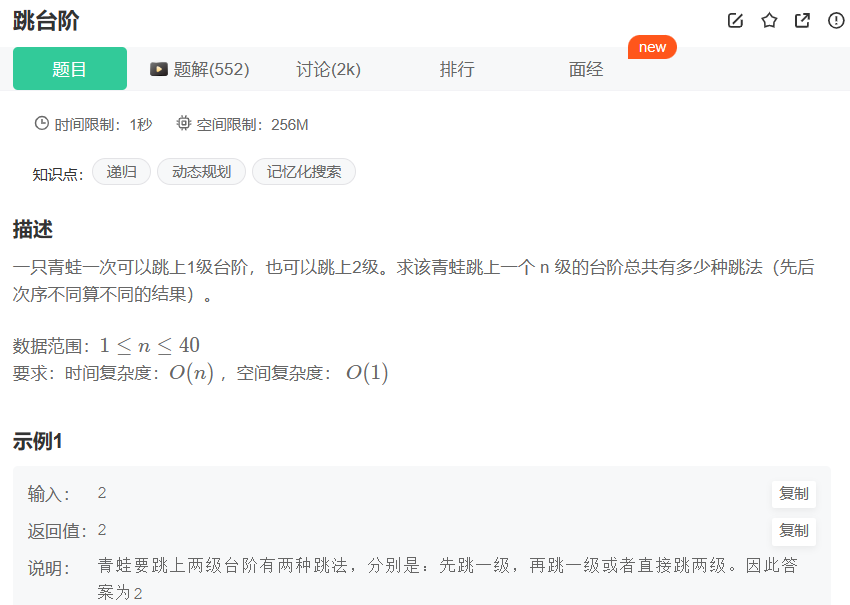
在青蛙跳台阶的问题中,如果把条件改成:一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级... ...它也可以跳上 n 级,此时该青蛙跳上一个 n 级的台阶总共有多少种跳法?
可以用数学归纳法证明:f(n) = 2^(n-1)。
力扣对应链接:70. 爬楼梯 - 力扣(LeetCode)
牛客对应链接:跳台阶_牛客题霸_牛客网
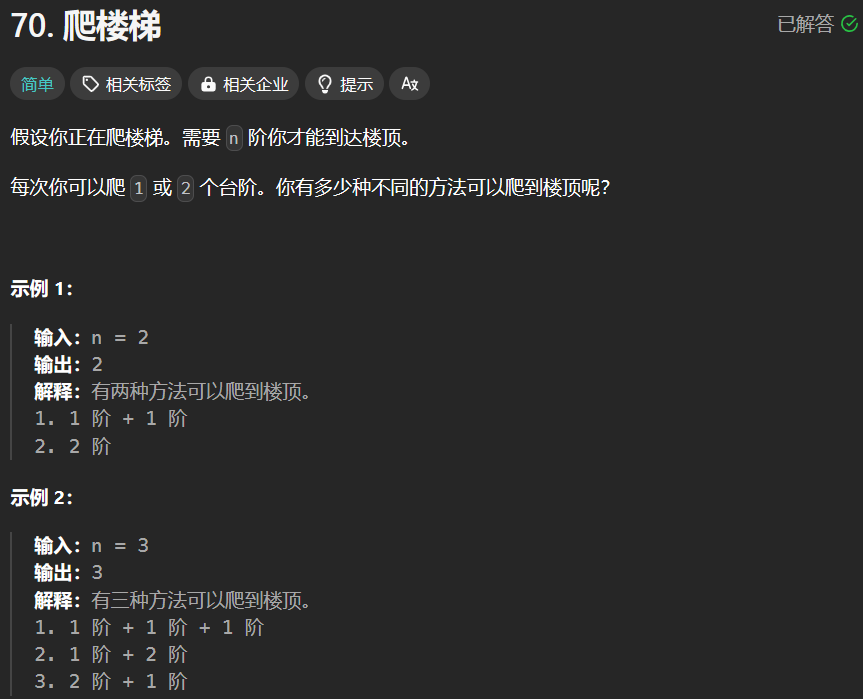
核心考点:场景转化模型,模型提取解法,简单 dp,fib。
1、分析题目
动规三步骤:
- 定义状态:f(n):青蛙跳上第 n 级台阶的总跳法数。(到了 n,只能是从 n-1 或 n-2 跳过上来)
- 编写状态转移方程:f(n) = f(n-1) + f(n-2)。
- 设置初始值:f(0) = 1(0 台阶就是起点,到达 0 台阶的方法有一种,就是不跳(这里可能有点奇怪,但是如果方法次数为 0,就说明不可能开始)),f(1) = 1,f(2) = 2。
2、代码
(1)方法一(动态规划)
//时间复杂度: O(n), 空间复杂度: O(N)
//牛客AC代码
class Solution {
public:
int jumpFloor(int number) {
//dp[n] = dp[n-1]+dp[n-2];
int dp[number+1];
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i<= number;i++)
dp[i] = dp[i-1] + dp[i-2];
return dp[number]; //第number下标,就是第number阶台阶
}
};
//力扣AC代码
class Solution {
public:
int climbStairs(int n) {
if(n<=2) return n;
vector<int> dp(n+1);
dp[0]=1, dp[1]=1, dp[2]=2;
for(int i=3; i<=n; i++)
dp[i]=dp[i-1]+dp[i-2];
return dp[n];
}
};(2)方法一(动态规划 + 优化)
//时间复杂度: O(n), 空间复杂度: O(1)
//牛客AC代码
class Solution {
public:
int jumpFloor(int number) {
int first=1; //第一个台阶
int second=2; //第二个台阶
int third=number; //等于number直接就考虑了dp[]1]=1 && dp[2]=2的情况
while(number>2)
{
third=first+second;
first=second;
second=third;
number--;
}
return third;
}
};
//力扣AC代码
class Solution {
public:
int climbStairs(int n) {
if(n<=2) return n;
int dp[3];
dp[0]=1, dp[1]=1, dp[2]=2;
for(int i=3; i<=n; i++)
{
int sum=dp[1]+dp[2];
dp[1]=dp[2];
dp[2]=sum;
}
return dp[2];
}
};六、举一反三
牛客对应链接:矩形覆盖_牛客题霸_牛客网 (nowcoder.com)

核心考点:场景转化成模型,特殊情况分析,简单 dp。
1、分析题目
比如 n = 3 时,2*3 的矩形块有 3 种不同的覆盖方法(从同一个方向看):
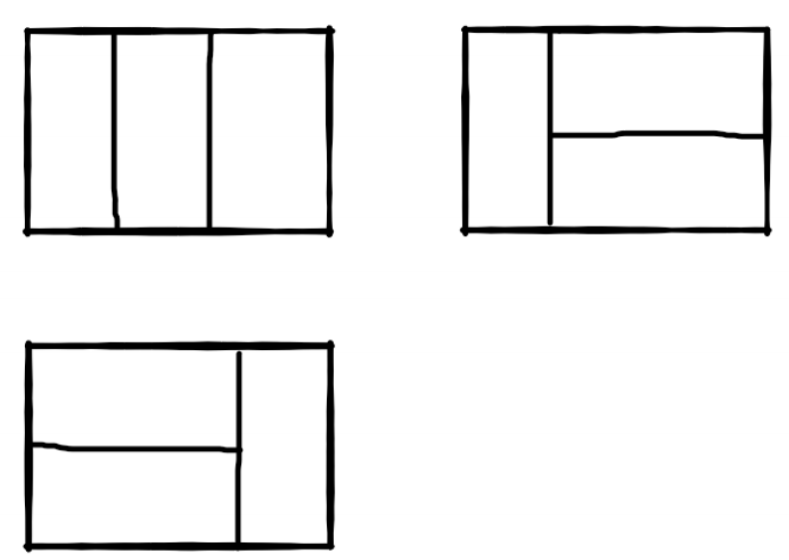
那如果是用 8 个 2*1 的小矩形无重叠地覆盖一个 2*8 的大矩形(右图),总共又有多少种方法?
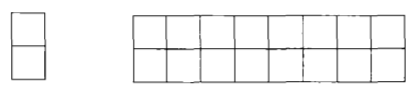
我们先把 2*8 的覆盖方法记为 f(8)。用第一个 1*2 小矩形去覆盖大矩形的最左边时有两个选择,竖着放或者横着放。当竖着放的时候,右边还剩下 2*7 的区域,这种情形下的覆盖方法记为 f(7)。接下来考虑横着放的情况。当 1*2 的小矩形横着放在左上角的时候,左下角必须和横着放一个 1*2 的小矩形,而在右边还剩下 2*6 的区域,这种情形下的覆盖方法记为 f(6),因此 f(8) = f(7) + f(6)。
这不就是斐波那切数列的问题吗?反思一下,很多问题会包裹很多现实问题,解决问题的第一步往往是从实际问题中提炼出我们的解决问题的数学模型,然后再进行解决。这里也可以使用多种方法解决,不过我们这里重点用 dp,倒也不是说它是最优的,而是平时在写代码的时候,这种思想还是用得少,所以就多写一写。
用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形,每次放置的时候,无非就两种放法,横着放或竖着放。
其中,横着放一个之后,下一个的放法也就确定了,所以虽然放置了两个矩形,但属于同一种放法。其中,竖着放一个之后,本轮放置也就完成了,也属于一种方法。
所以,当 2*n 的大矩形被放满的时候,它无非就是从上面两种放置方法放置来的。
下面继续使用 dp 来进行处理,我们发现斐波那契数列的方式也可以处理,因为前面已经讲过,这里就不再用这种方式来写了
- 状态定义:f(n) : 用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形所用的总方法数。
- 状态递推:f(n) = f(n-1)【最后一个竖着放】 + f(n-2)【最后两个横着放】。
- 初始化:f(0) = 1(f(0) 这里可以不考虑,因为语义不清淅,如果考虑的话就把值设为 1,可参考前面的原因),f(1) = 1,f(2) = 2。
注意:这里需要充分考虑 n 是 [0,1] 时的情况,OJ 一般测试用例设计的比较全面,会有 0,1 传进来,这个时候后续的 dp[1] = 1; 就可能报错。
2、代码
(1)方法一(动态规划)
//牛客AC代码
class Solution {
public:
int rectCover(int number) {
if(number<=2)
return number;
int dp[number+1];
dp[1]=1, dp[2]=2;
for(int i=3; i<=number; i++)
dp[i] = dp[i-1]+dp[i-2];
return dp[number];
}
};