原理分析

可以将路径每个连续的两点向量叉乘相加，根据正负性判断路径顺逆时针性
当我们计算两个向量的叉积时，结果是一个新的向量，其方向垂直于这两个向量所在的平面，并且其大小与这两个向量构成的平行四边形的面积成正比。这个新向量的方向由右手定则确定：如果你将右手的四指放在两个向量的方向上，让拇指指向叉积的方向，那么你的手指弯曲的方向就是两个向量的顺时针旋转方向。

当我们应用这个概念到路径的情况时，我们可以将相邻的路径点表示为向量，然后计算它们之间的叉积。这个叉积的 z 分量（如果我们将路径投影到 xy 平面上）可以告诉我们这两个向量之间的顺时针或逆时针关系。

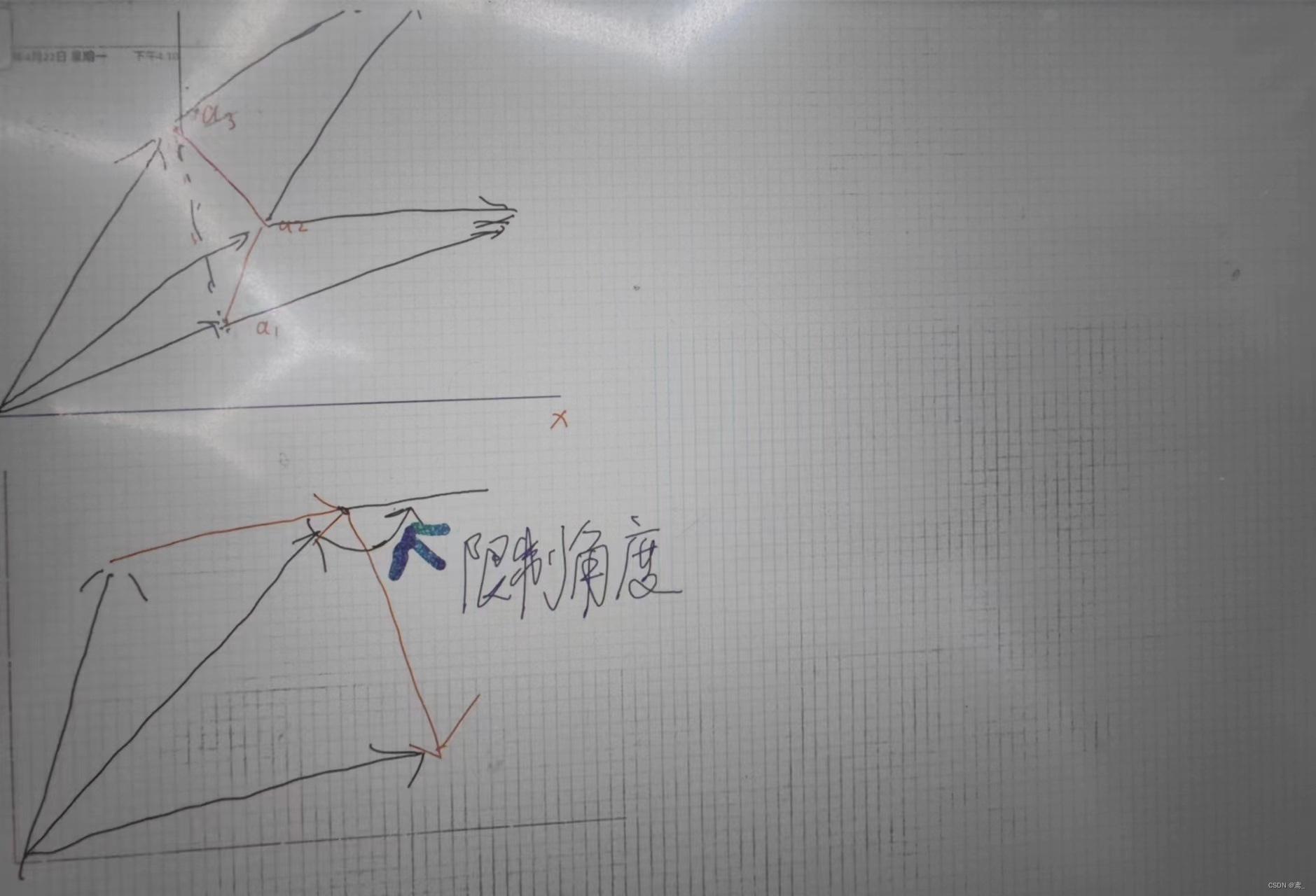
由于threejs很多地方对凹凸多边形没有限制，可以在输入端限制凹三角或在计算中舍弃凹点

代码

import { Vector3 } from "three";

/**
 * 判断向量是否为顺时针  返回值true逆时针  false 顺时针
 * @param {[Vector3]} path //vec3路径
 * @param {'x'|'y'|'z'} forword //基准
 * @returns 
 */
export default function isClockwise(path, forword = 'z') {
    let sum = 0;
    const n = path.length;

    for (let i = 0; i < n; i++) {
        const current = path[i];
        const next = path[(i + 1) % n]; // 取下一个点，循环到第一个点

        // 计算当前点到下一个点的向量
        const vector = next.clone().sub(current);

        // 只考虑 xy 平面上的向量，忽略 z 分量
        vector.z = 0;

        // 叉积的 z 分量可以判断顺时针还是逆时针
        if (forword == 'z')
            sum += (current.x * next.y - next.x * current.y);
        else if (forword == 'x')
            sum += (current.z * next.y - next.z * current.y);
        else if (forword == 'y')
            sum += (current.x * next.z - next.x * current.z);
	
		/**
		*如果业务需要 可以在这里判断sum大小变化确定 如果增或者减反向 则可判断这里出现凹点
		*/
    }

    // 如果 sum 大于 0，则路径是逆时针的；如果 sum 小于 0，则路径是顺时针的
    return sum > 0;
}

使用

使用isClick判断路径方向性，并转为顺时针

   let reverse = isClockwise(vertices)
    if (reverse) vertices.reverse()