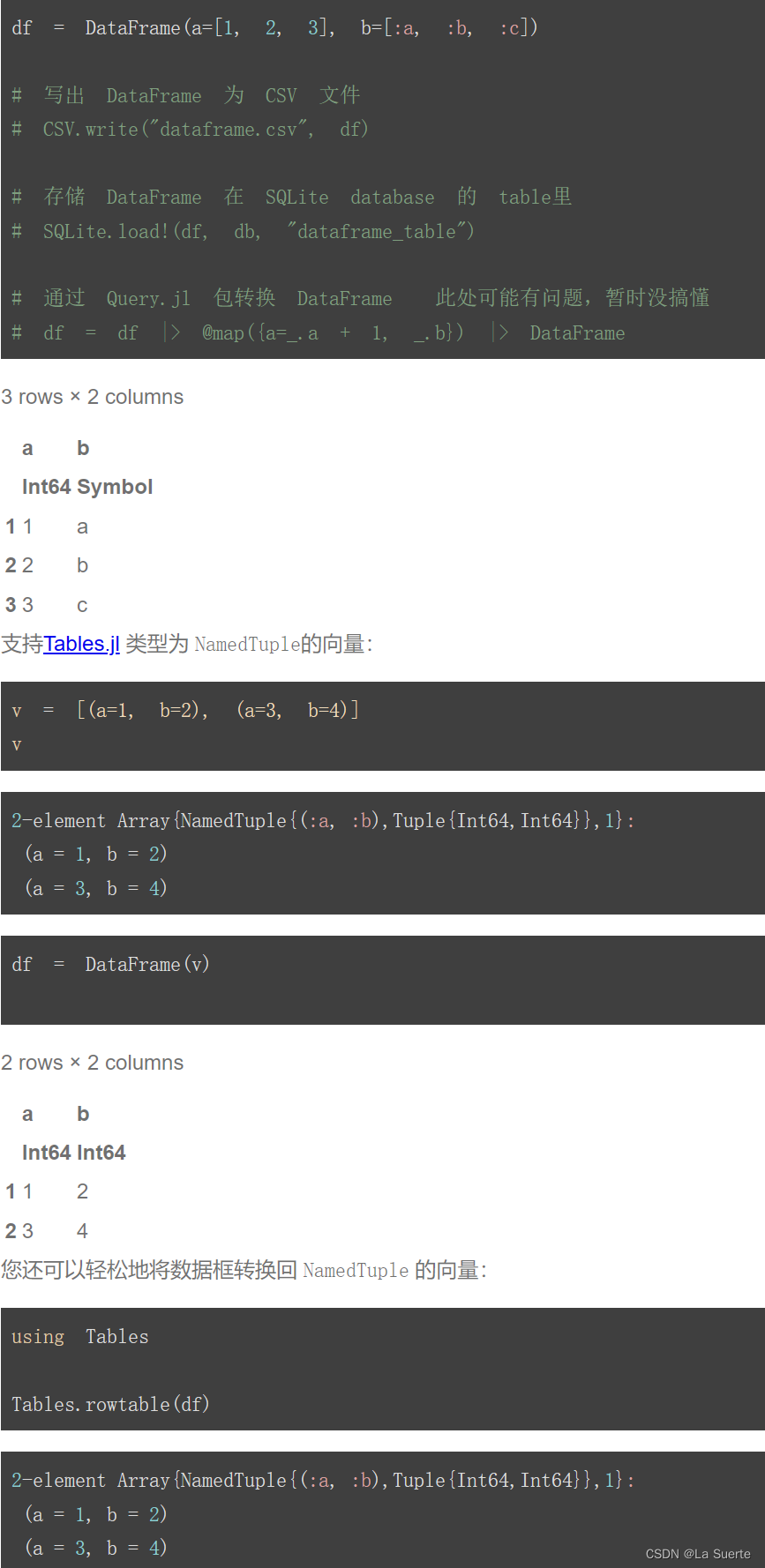
前言:本节内容属于数据结构的入门知识——算法的时间复杂度和空间复杂度。
时间复杂度和空间复杂度的知识点很少, 也很简单。 本节的主要篇幅会放在使用具体例题来分析时间复杂度和空间复杂度。本节内容适合刚刚接触数据结构或者基础有些薄弱的友友们哦。
衡量一个算法的性能
我们用什么来衡量一个算法的性能呢? 其实就是用到了时间复杂度和空间复杂度。 时间复杂度是一个时间的量度, 它用来衡量一个算法的快慢程度; 空间复杂度是一个空间的量度, 它用来衡量一个算法所需要的空间多少。、
算法的时间复杂度和空间复杂度都是一个函数, 这个函数并不是数学中的函数, 是在计算机科学之中进行定义的。 对于时间复杂度来说, 时间复杂度描述的是一个算法的执行次数; 对于空间复杂度来说, 空间复杂度描述的是一个算法在运行过程中额外开辟的空间个数。
执行次数:这里的这个概念很重要, 什么是执行次数? 执行次数就是一个算法中循环的的次数。 例如如图的代码:
void test()
{
for (int i = 0; i < 10; i++)
{
printf("%d\n", i);
}
}
图中的循环有10次, 所以执行次数就是10。这就是执行次数的概念。
空间消耗:其实随着科技的进步, 现在的计算机的硬件已经非常优秀了。 所以一个算法对于空间消耗的关注不再像以前那样关注。 但是, 这里我们还是要知道空间消耗的概念。我们看一个实例:
void test1()
{
int i = 0;
int a = 0;
int b = 0;
scanf("%d %d %d", &a, &b, &i);
printf("%d %d %d", a, b, i);
}
图中创建了三个变量, 所以空间消耗就是3, 这就是空间消耗的概念。
表示方法
时间复杂度和空间复杂度的表示方法使用了大O的渐进表示法。 什么时大O的渐进表示法?
我们在上文中说过, 算法的时间复杂度和空间复杂度都是一个函数, 但是与数学的函数又有所区别。 其实, 大O的渐进表示法就可以使用这个函数来理解。
时间复杂度
我们这里将使用具体的实例来分析算法的时间复杂度:
void func1()
{
int N;
scanf("%d", &N);
for (int i = 0; i < N; i++)
{
printf("%d", i);
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
printf("%d", j);
}
printf("\n");
}
}
int main()
{
func1();
return 0;
}
时间复杂度的计算其实就是计算算法的执行次数, 由上文的执行次数的概念我们知道func1算法的执行次数是N^2 + N。
那么利用大O的渐进标识法表示后,算法func1的时间复杂度就是O(N^2)。由此我们可以见到N^2 + N使用大O的渐进表示法之后, 只保留了最大项。这里的N^2 + N中的N为什么会被省略, 我们接下来会进行讲解:
对于上面的算法来说: 执行次数是N^2 + N, 对于这里的N我们取三个值进行分别讨论: 一个是当N == 10的时候, 第二个是当N == 10000的时候, 第三个是当N == 1000000的时候。
现在我们先来看当N == 10的时候。 那么N ^ 2 是100, N 是10。 这个时候两者的差距不大。 我们使用程序来跑一下, 下面是测试过程:
测试时间差距需要使用头文件time.h里面的一个函数: clock(), 这个函数的作用是返回从程序的开始到该执行语句所经历的时间。 并且这个返回值的单位是毫秒。
如图为我们进行测试执行次数N^2和N的时间差距:
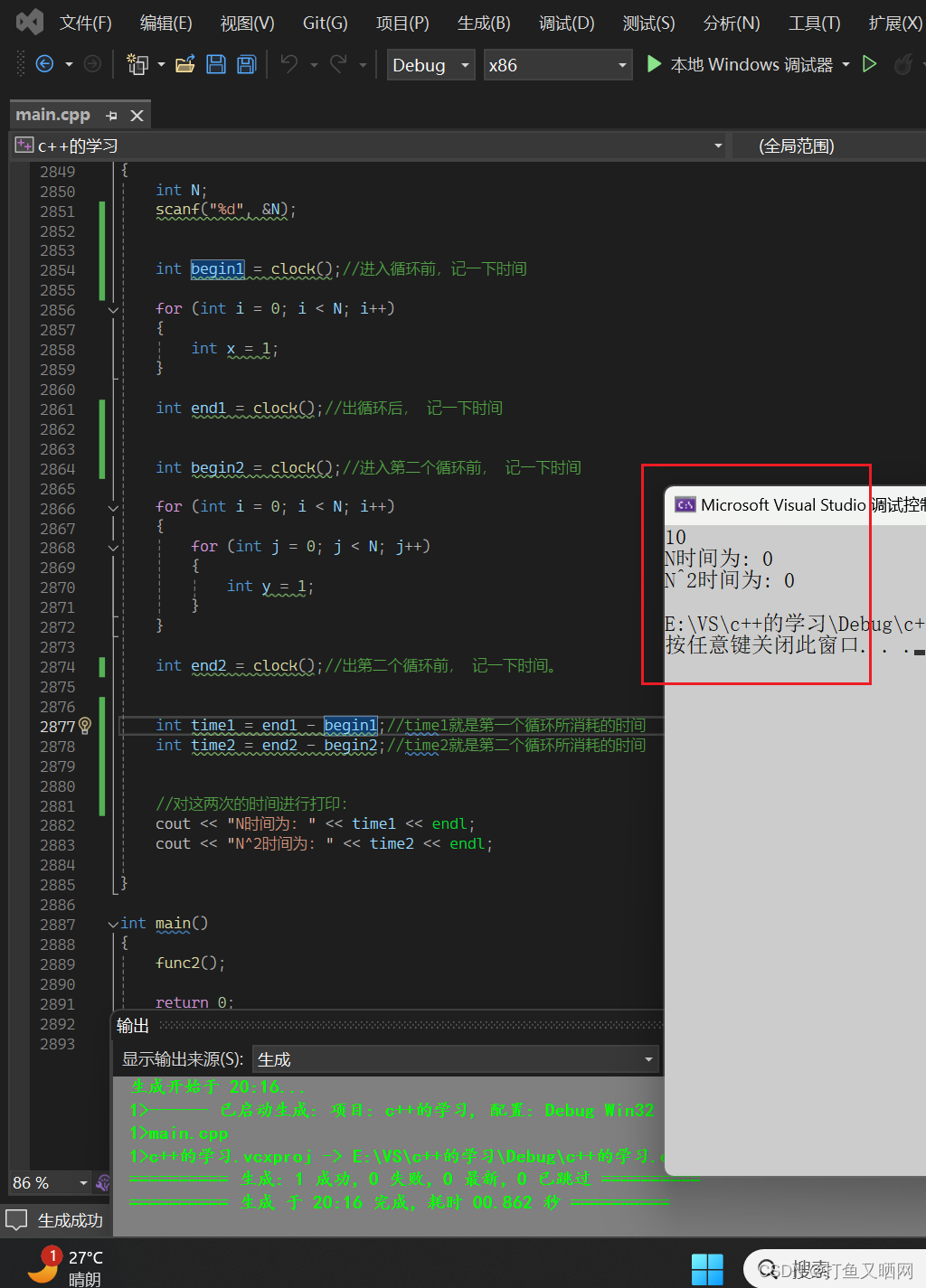
#include<time.h> void func2() { int N; scanf("%d", &N); int begin1 = clock();//进入循环前,记一下时间 for (int i = 0; i < N; i++) { int x = 1; } int end1 = clock();//出循环后, 记一下时间 int begin2 = clock();//进入第二个循环前, 记一下时间 for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { int y = 1; } } int end2 = clock();//出第二个循环前, 记一下时间。 int time1 = end1 - begin1;//time1就是第一个循环所消耗的时间 int time2 = end2 - begin2;//time2就是第二个循环所消耗的时间 //对这两次的时间进行打印: cout << "N时间为: " << time1 << endl; cout << "N^2时间为: " << time2 << endl; } int main() { func2(); return 0; }
如图可见, 两者的时间都是0, 说明N == 10对cpu来说太小了, 我们加大N的大小。
下面测试第二组: N = 10000.
如图为第二组的测试结果。 在这组测试中, 第一个循环执行了N == 10000次, 消耗的时间小于1毫秒。
第二个循环执行了1亿次, 消耗的时间为24毫秒。
那么到现在我们其实已经可以稍微有点发现:当N变得越来越大时, N^2所消耗的时间是远远大于N的。
上面的第二次测试可能还不明显, 现在我们来看一下第三次测试, 这一次的N == 1000000, 也就是N 为 一百万, N^2为1万亿的时候。(ps : 这个时候其实已经需要跑很久了。)
由图可以看到, 其实第一个循环, cpu只用了1毫秒就完成了, 而第二个循环,cpu用了6分钟的时间。 而1毫秒相对于6分钟是可以省略的, 所以当N为一百万的时候我们可以不考虑第一个循环, 也就是不考虑N, 只需要考虑N ^ 2即可。
而且,我们也能看出来, cpu的执行速度是很高的。 在上面cpu执行一亿次循环也只用了二十几毫秒。 所以, 当N很小的时候, 我们是不关心的, 我们只关心当N很大的时候, 像后面的一百万。 而当N为一百万的时候, 第一个循环我们是可以忽略的。 所以对于N^2 + N的执行次数来说, 他的时间复杂度就是O(N^2)。
所以, 综上, 大O的渐进表示法, 考虑的是当N极大时的情况, 当N很小时我们不进行考虑。 所以, 我们在使用大O的渐渐表示法的时候, 如果有了关于N的函数, 我们只去最大项。
本节的知识点内容很少, 主要是使用例题来学习如果使用大O的渐进表示法, 下面我们来看例题
例题1:
计算如图的时间复杂度
void test1(int n) { int x = 0; for (int i = 0; i < n; i++) { x++; } int k = 10; for (int i = 0; i < k; i++) { x++; } }解析: 如图中有两个循环, 第一个循环是从i = 0到 n。 第二个循环的执行次数是10, 那么可以得到执行次数为 : n + 10, 那么使用大O的渐进表示法取最大项就是O(n)。
例题2:
计算如图的时间复杂度
void test2(int n, int k) { int x = 0; for (int i = 0; i < n; i++) { x++; } for (int i = 0; i < k; i++) { x++; } }解析:如图有两个未知量, 一个是n, 一个是k, 同时有两个循环, 第一个循环是从0~n, 第二个循环是从0~k, 那么他一共的执行次数就是n + k。 并且由于n和k都不是常数, 他们同时都是未知量。 所以时间复杂度就是O(n + k)。
例题3:
计算如图的时间复杂度
void test3(int n) { int x = 0; for (int i = 0; i < 50; i++) { x++; } }解析:图中虽然有位置量n, 但是图中的循环执行是从i = 0到50, 也就是执行次数为50. 执行次数永远为一个常数。 而常数级别使用大O的渐进表示法我们规定是: O(1)。 这就代表常数级别的时间复杂度。
例题4:
计算冒泡排序的时间复杂度:
//本串代码不是原创, 是从本人学习的课件中搬运而来。如果和别人的相同, 属于巧合。非是抄袭。 void BubbleSort(int* a, int n) { for (size_t end = n; end > 0; --end) { int exchange = 0; for (size_t i = 1; i < end; ++i) { if (a[i - 1] > a[i]) { swap(a[i - 1], a[i]); exchange = 1; } } if (exchange == 0) break; } }解析: 冒泡排序有两层循环, 第二层循环的执行次数会随着第一层循环执行次数的增长而减小。 根据推到, 我们其实可以计算出冒泡排序的执行次数是这样的 : (n - 1) + (n - 2) + (n - 3) + (n - 4) + (n - 5) + …… + 1 = n^2 / 2;
如果最大项带有系数, 就像现在的n^2 / 2, 我们一般都是将它的系数省略。 所以冒泡的时间复杂度就是O(n^2)。
例题5
计算如图的时间复杂度
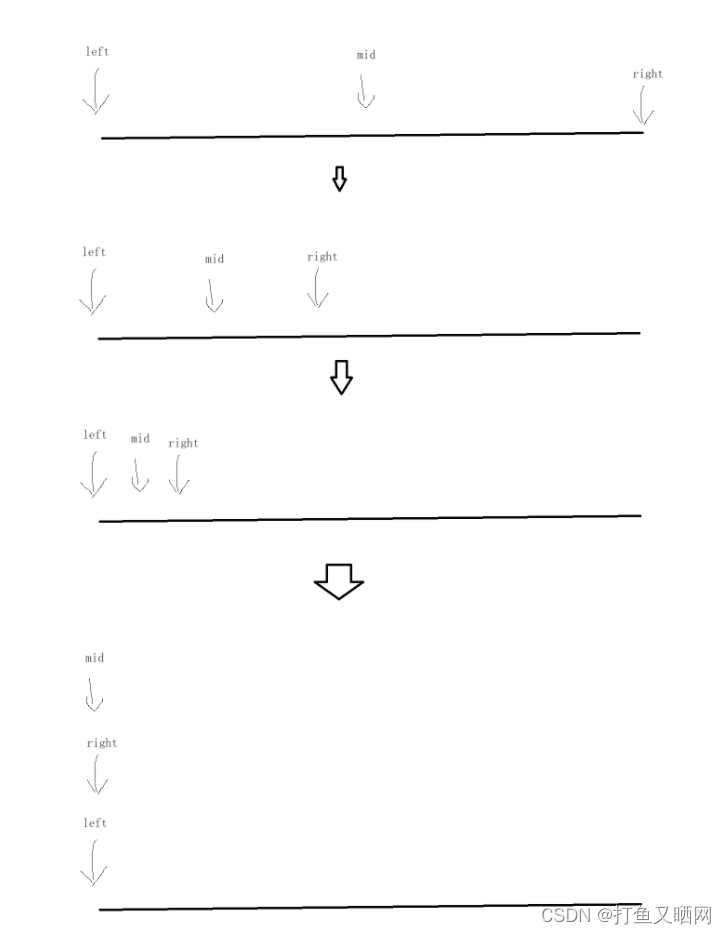
//本串代码不是原创, 是从本人学习的课件中搬运而来。如果和别人的相同, 属于巧合。非是抄袭。 int BinarySearch(int* a, int n, int x) { int begin = 0; int end = n - 1; while (begin <= end) { int mid = begin + ((end - begin) >> 1); if (a[mid] < x) begin = mid + 1; else if (a[mid] > x) end = mid - 1; else return mid; } return -1; }解析 : 同种是一个朴素二分查找的算法, 对于这个算法来说, 最坏的一种情况就是当左右指针相等的时候才找到要寻找的值。 如图:
而这种情况下我们可以假设执行次数是k次, 那么就有2 ^ k = n, 所以它的执行次数计算出来就是lgn, 所以二分算法的时间复杂度就是O(lgn)。
以上, 就是时间复杂度的全部例题, 下面开始讲解空间复杂度。
空间复杂度
空间复杂度同样是使用大O的渐进表示法进行标识, 同时规则和时间复杂度的一样, 我们只考虑最大项即可。
我们直接通过例题来进行空间复杂度的学习:
例题1
计算下面算法的空间复杂度:
//本串代码不是原创, 是从本人学习的课件中搬运而来。如果和别人的相同, 属于巧合。非是抄袭。 void BubbleSort(int* a, int n) { for (size_t end = n; end > 0; --end) { int exchange = 0; for (size_t i = 1; i < end; ++i) { if (a[i - 1] > a[i]) { swap(a[i - 1], a[i]); exchange = 1; } } if (exchange == 0) break; } }还是冒泡排序, 计算这个排序算法的空间复杂度。 在计算空间复杂度之前, 我们需要想清楚一件事情:空间复杂度计算的是什么?
这里要强调: 空间复杂度计算的是额外空间!额外空间!额外空间!
那么, 既然空间复杂度计算的是额外空间, 冒泡排序中的参数n, 还有数组a, 就不算在空间复杂度中。 为什么会这样?
这里要想明白一个问题, 我们在计算空间复杂度的时候, 计算的是这个算法的空间复杂度。 但是, 对于数组a和参数n来说, 任何一个算法设计,我们是不是都要使用参数接收他们?他们是不可能避免的。 是不属于这个算法的。 所以, 我们说数组a和参数n不算在空间复杂度中。
那么再回过头去看我们的冒泡排序, 在这个排序中, 我们只开了三个变量: end, i, exchange。 那么它的空间复杂度就是O(1)。
例题2
计算下面算法中的空间复杂度
//本串代码不是原创, 是从本人学习的课件中搬运而来。如果和别人的相同, 属于巧合。非是抄袭。 long long* Fibonacci(size_t n) { if (n == 0) return NULL; long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long)); fibArray[0] = 0; fibArray[1] = 1; for (int i = 2; i <= n; ++i) { fibArray[i] = fibArray[i - 1] + fibArray[i - 2]; } return fibArray; }解析: 首先malloc开辟了n + 1个long long类型的空间。 然后for循环中创建了一个int i 的变量。 所以一共二外开辟了n + 2个空间。 所以空间复杂度是O(n)。
空间复杂度的内容较少, 实际上, 因为硬件的发展。人们对于空间复杂度的关注已经少于时间复杂度。当然, 也有一些比如单片机领域就会注重空间复杂度。但是, 在本节中关于空间复杂度的讲解已经完毕。
以上, 后续会添加一个复杂度系数的对比图。 (待博主学会画图再来)