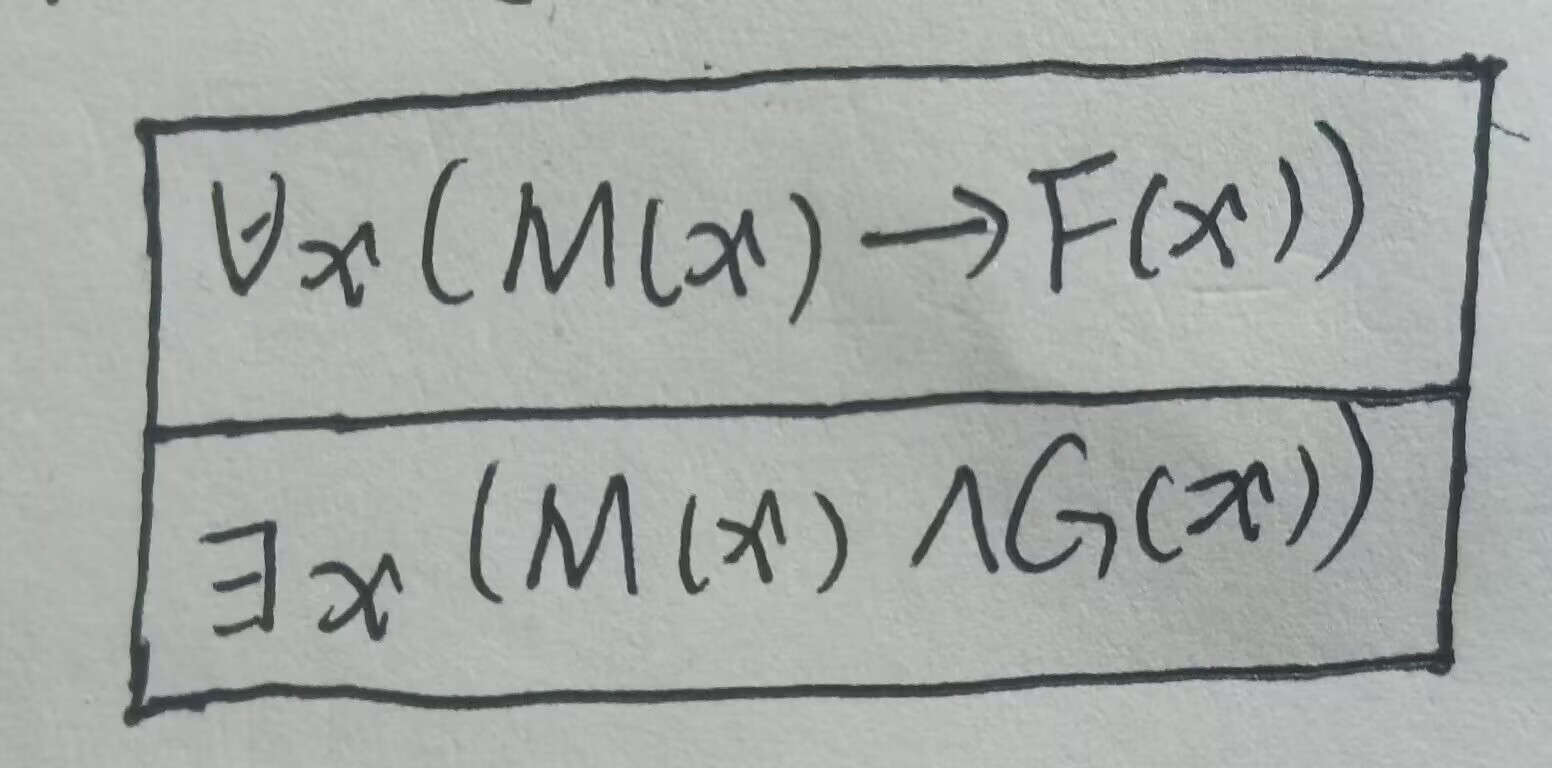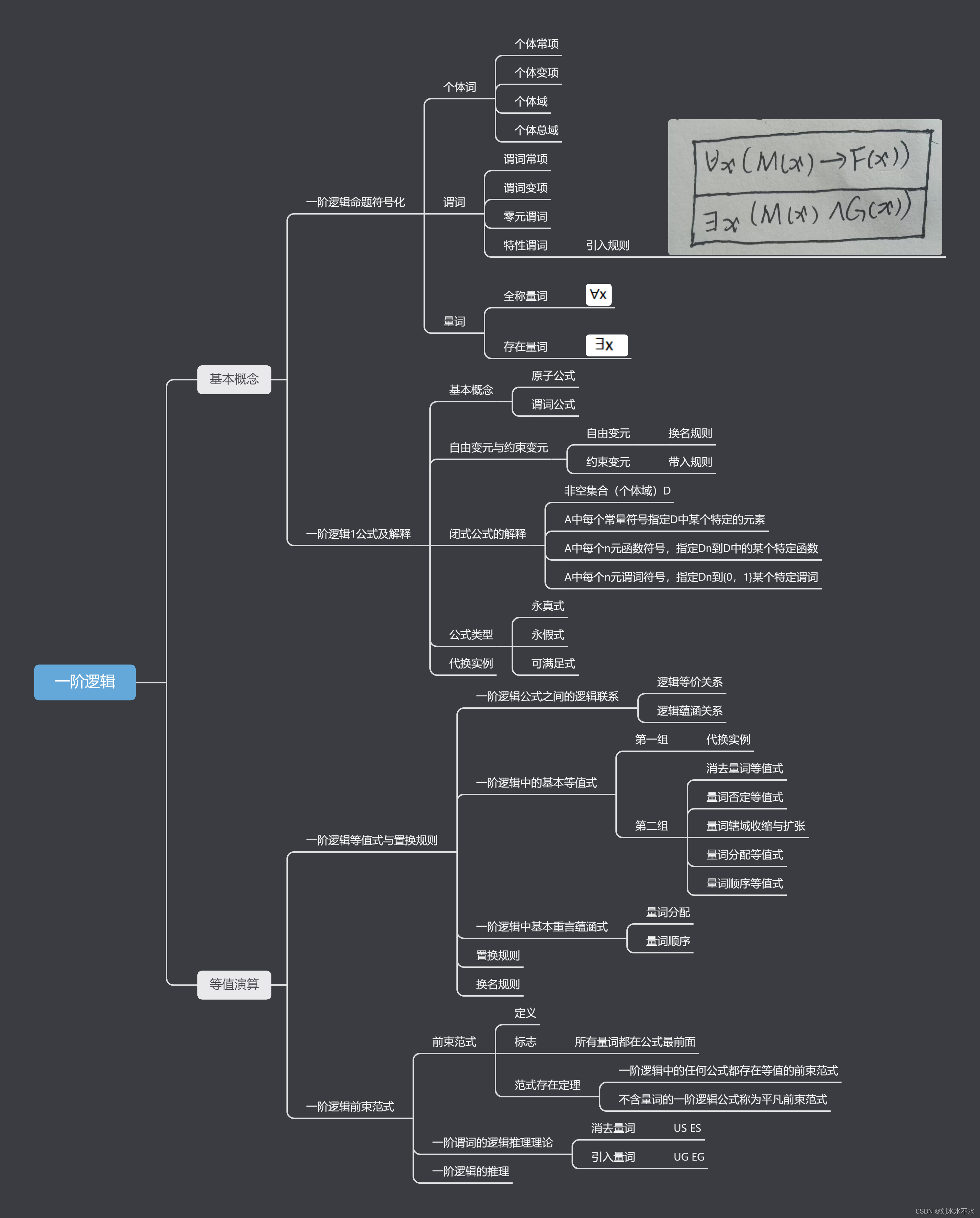
大纲笔记
- 基本概念
- 一阶逻辑命题符号化
- 个体词
- 个体常项
- 个体变项
- 个体域
- 个体总域
- 谓词
- 谓词常项
- 谓词变项
- 零元谓词
- 特性谓词
- 引入规则
-
- 引入规则
- 量词
- 全称量词
-
- 存在量词
-
- 全称量词
- 个体词
- 一阶逻辑1公式及解释
- 基本概念
- 原子公式
- 谓词公式
- 自由变元与约束变元
- 自由变元
- 换名规则
- 约束变元
- 带入规则
- 自由变元
- 闭式公式的解释
- 非空集合(个体域)D
- A中每个常量符号指定D中某个特定的元素
- A中每个n元函数符号,指定Dn到D中的某个特定函数
- A中每个n元谓词符号,指定Dn到{0,1}某个特定谓词
- 公式类型
- 永真式
- 永假式
- 可满足式
- 代换实例
- 基本概念
- 一阶逻辑命题符号化
- 等值演算
- 一阶逻辑等值式与置换规则
- 一阶逻辑公式之间的逻辑联系
- 逻辑等价关系
- 逻辑蕴涵关系
- 一阶逻辑中的基本等值式
- 第一组
- 代换实例
- 第二组
- 消去量词等值式
- 量词否定等值式
- 量词辖域收缩与扩张
- 量词分配等值式
- 量词顺序等值式
- 第一组
- 一阶逻辑中基本重言蕴涵式
- 量词分配
- 量词顺序
- 置换规则
- 换名规则
- 一阶逻辑公式之间的逻辑联系
- 一阶逻辑前束范式
- 前束范式
- 定义
- 标志
- 所有量词都在公式最前面
- 范式存在定理
- 一阶逻辑中的任何公式都存在等值的前束范式
- 不含量词的一阶逻辑公式称为平凡前束范式
- 一阶谓词的逻辑推理理论
- 消去量词
- US ES
- 引入量词
- UG EG
- 消去量词
- 一阶逻辑的推理
- 前束范式
- 一阶逻辑等值式与置换规则