第 12 讲 图、网络、关联矩阵
Graphs,networks,incidence matrices
本讲讨论线性代数在物理系统中的应用。
图和网络 Graphs & Networks
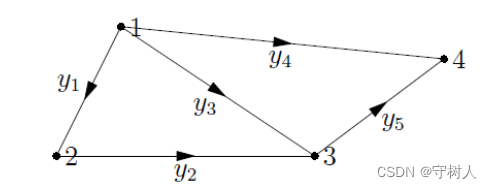
“图”就是“结点”和“边”的一个集合。
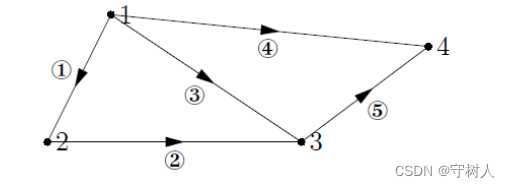
边线上的箭头代表从结点流出的正方向。
关联矩阵(Incidence matrices)
构造一个矩阵来表示图的内在含义,此矩阵称为关联矩阵,图中每个结点代表
一列,每边代表一行。则上图为 54 矩阵。反过来从这个矩阵出发我们也能画出图。

第一行代表边①,从结点 1 流出记为-1,从结点 2 流入记为 1。 边①,边②和边③构成了一个回路,称为环(loop)。反映在矩阵上是这三个行向量线性相关。
源于现实问题的关联矩阵,通常描述了问题的结构。如果我们研究一个很大的图,则会构建一个很大的矩阵,但这个矩阵会是稀疏矩阵。
考察矩阵的零空间,即求 Ax=0 的解。零空间告诉我们列向量线性组合的状态。

如果 x 为结点上的电势,则 Ax 给出了每个边上的电势差。求解可以得到零空间为一维 dim N(A)=1,它的基就是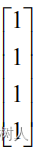
,解集则是 x=c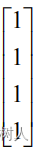
,代表等电势,说明等电势条件下不会有电流产生。常数 c 的确定需要边界条件,比如我们将结点 4 接地则 x4=0。
若求 Ax=b 的解,则相当于在给定了电压 b 的情况下,求各点的电势,但实际上我们得不到电势的准确值,因为零空间有常数解 c,各点得到的电势需要加上常数 c,这很类似于求积分要加上常函数,常数值需要边界条件来确定。
矩阵的列数为 4,而其零空间的维数为 1,则矩阵的秩为 3,矩阵第 1 列,第 2列,第 4 列的列向量线性无关。
矩阵的左零空间是满足 ATy=0 的向量 y 的集合。因为矩阵 AT有 5 列,矩阵
的秩为 3,因此矩阵的左零空间维数为 2。这反应了行向量的线性关系,整个“图”中,环数为 2。
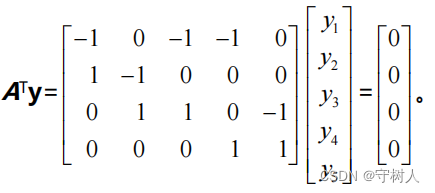
y 的分量的值为“边”上的电流。
在电势差和电流之间建立联系就是欧姆定律(Ohm’s Law)

我们求解 ATy=0 就是在求 5 个满足基尔霍夫电流定律(Kirchhoff’s Law)的电流值。
ATy=0 的方程形式 ,每一个方程关于一个结点,方程表示结点电流值为 0,即流入等于流出。
,每一个方程关于一个结点,方程表示结点电流值为 0,即流入等于流出。
从图上解方程,而不是采用消元法解方程。如果我们设定 y1=1,并且让 y1,y2和 y3组成的回路的“环流“为 0,则有 y2=1,y3=-1。可解得 y=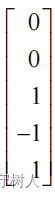
。取另一个回路的环流为 0,则有 y3=1,y4=-1,y5=1。y=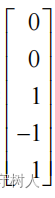
如果设定 y1,y2,y4 和 y5 组成的大回路环流为 0,则可以得到另一个向量 y,而该向量在零空间内,是前两个向量的线性组合。
考察矩阵的行空间,因为矩阵 r=3,所以存在 3 个线性无关的向量。第 1 行,第 2 行和第 4 行为线性无关,在“图”中,边①,边②和边④构成了一张小图,这三个边没有形成回路。线性相关问题等价于形成回路。没有回路的小图包含 4 个结点和 3 条边,再添加一条边就会产生回路,在矩阵里表现为在第 1 行,第 2 行和第 4行之上再添加一个行向量就会变为线性相关。没有回路的图称为“树”。
思考一下维数公式的在“图”中的意义:
左零空间维数 dim N(AT)=m-r;
等价于“环”数量=“边”数量-(“结点”数量-1);
即 Eular 公式:“结点”-“边”+“环”=1。对所有图都成立。
矩阵的秩 r=“结点”-1,因为 r 表示了线性无关的边的数目,也就是“树”中“边”的数目。

之前的讨论都是针对于一个无源的电场,如果加入电源则情况又不同,例如加入电流源相当于将基尔霍夫定律的方程变为 ATy=f,f 就是外部流入的电流。