《动手学深度学习(Pytorch版)》Task02:预备知识——4.25打卡
- 数据操作
- N维数组——张量
- 创建数组
- 访问元素
- 入门
- 初始化矩阵
- 运算符
- 广播机制
- 索引和切片
- 节省内存
- 转换为其他Python对象
- 转换为NumPy张量`ndarray`
- 张量转换为Python标量
- 数据预处理
- 安装pandas
- 读取数据集
- 处理缺失值
- 转换为张量格式
- 删除缺失值最多的列
- 线性代数
- 标量
- 向量
- 长度、维度和形状
- 矩阵
- 范数
- 特殊矩阵
- 特征向量和特征值
- 张量
- 降维
- 非降维求和
- 点积(Dot Product)——标量
- 矩阵-向量积
- 矩阵-矩阵乘法
- 范数
- 微积分
- 导数和微分
- 亚倒数
- 偏导数
- 梯度
- y是标量x是向量
- y是向量x是标量
- y是向量x是向量
- 链式法则
- 自动求导
- 两种模式
- 复杂度
- 分离计算
- Python控制流的梯度计算
数据操作
对应代码文件
N维数组——张量
N维数组是机器学习和神经网络的主要数据结构
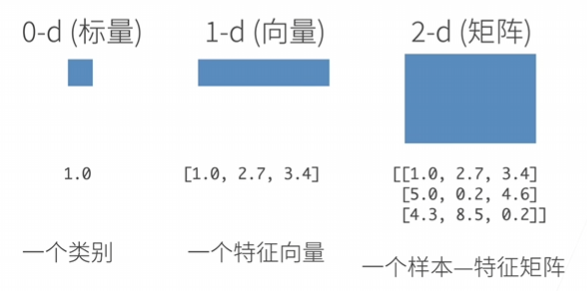
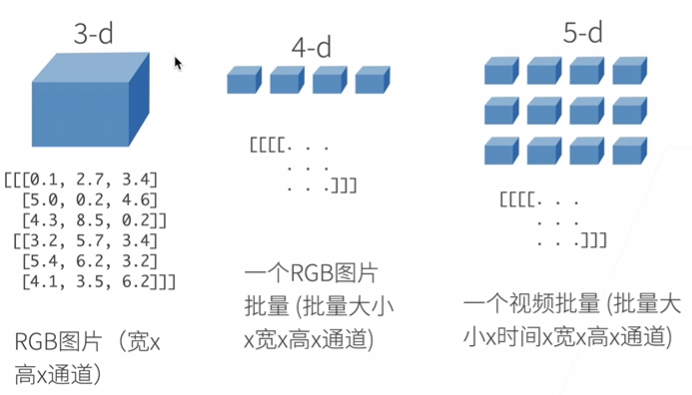
创建数组
- 形状:例如 3x4矩阵
- 每个元素的数据类型:例如32位浮点数
- 每个元素的值:例如全是0,或者随机数
访问元素
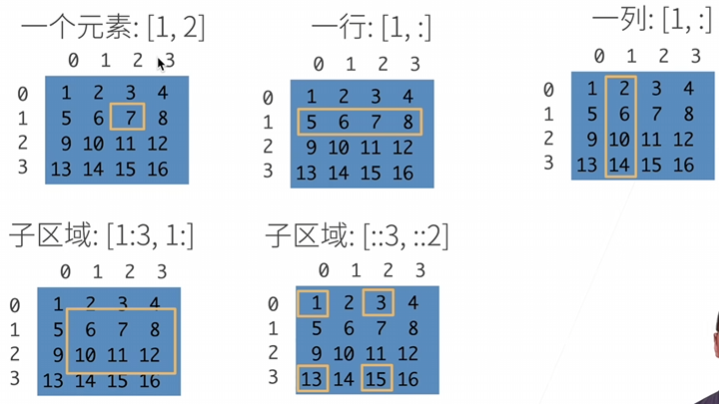
:访问一行全部
::3间隔为3跳着访问
入门
导入torch
import torch
创建行向量
x = torch.arange(12)
访问张量(沿每个轴的长度)的形状
x.shape
求张量中元素的总数
# 元素总数,标量
x.numel()
改变一个张量的形状而不改变元素数量和元素值
X = x.reshape(3, 4)
通过-1来调用此自动计算出维度的功能
x.reshape(-1,4)
初始化矩阵
张量所有元素都设置为0
# 全0
torch.zeros((2, 3, 4))
张量所有元素都设置为1
# 全1
torch.ones((2, 3, 4))
随机初始化参数
torch.randn(2,3,4)
用Python列表为每个元素赋予确定值
torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
运算符
标准算术运算符(+、-、\*、/和\**)都可以被升级为按元素运算
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y # **运算符是求幂运算
指数运算:计算e的x次幂, e x e^x ex
torch.exp(x)
多个张量连结(concatenate)在一起
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
dim=0表示在行上进行连接
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 2., 1., 4., 3.],
[ 1., 2., 3., 4.],
[ 4., 3., 2., 1.]]),
dim=1表示在列上进行连接
tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
[ 4., 5., 6., 7., 1., 2., 3., 4.],
[ 8., 9., 10., 11., 4., 3., 2., 1.]]))
通过逻辑运算符构建二元张量
X == Y
求和,产生一个单元素张量
X.sum()
out: tensor(66.)
广播机制
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a和b分别是3×1和1×2矩阵,如果让它们相加,它们的形状不匹配。
方法:两个矩阵广播为一个更大的3×2矩阵,矩阵a将复制列, 矩阵b将复制行,然后再按元素相加。
索引和切片
元素可以通过索引访问。
第一个元素的索引是0,最后一个元素索引是-1
可以指定范围以包含第一个元素和最后一个之前的元素。
X[-1], X[1:3]
通过指定索引来将元素写入矩阵,给固定位置的索引赋值
X[1, 2] = 9
给多个位置索引赋值
X[0:2, :] = 12
节省内存
id()函数:提供内存中引用对象的确切地址
before = id(Y)
Y = Y + X
id(Y) == before
out: False
Python为结果分配新的内存
我们希望原地执行这些更新
Z = torch.zeros_like(Y) # 和Y的shape数据类型一致,但元素是0
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))
没有重复使用X时,可以使用X[:] = X + Y或X += Y来减少操作的内存开销。
before = id(X)
X += Y
id(X) == before
转换为其他Python对象
转换为NumPy张量ndarray
torch张量和numpy数组将共享它们的底层内存
A = X.numpy()
B = torch.tensor(A)
张量转换为Python标量
item函数或Python的内置函数。
a = torch.tensor([3.5])
a.item(), float(a), int(a)
数据预处理
学习pandas预处理原始数据,并将原始数据转换为张量格式的步骤。
安装pandas
pip install pandas
读取数据集
创建一个人工数据集,并存储在CSV
import os
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
NA:未知
属性:
- 房间数量(“NumRooms”)
- 巷子类型(“Alley”)
- 房屋价格(“Price”)
import pandas as pd
data = pd.read_csv(data_file)
print(data)
处理缺失值
NaN项代表缺失值。
- 插值法:用一个替代值弥补缺失值
- 删除法:直接忽略缺失值
iloc:index location
#将data分成inputs和outputs,其中前者为data的前两列,而后者为data的最后一列
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
#对于inputs中缺少的数值,我们用同一列的均值替换“NaN”项
inputs = inputs.fillna(inputs.mean())
对于inputs中的类别值或离散值,我们将NaN视为一个类别。
pd.get_dummies: 对离散型特征进行one-hot编码,将每个取值转换成一个独立的状态。
dummy_na=True: NaN值设为True
inputs = pd.get_dummies(inputs, dummy_na=True)
NumRooms Alley_Pave Alley_nan
0 3.0 1 0
1 2.0 0 1
2 4.0 0 1
3 3.0 0 1
转换为张量格式
import torch
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X, y
(tensor([[3., 1., 0.],
[2., 0., 1.],
[4., 0., 1.],
[3., 0., 1.]], dtype=torch.float64),
tensor([127500, 106000, 178100, 140000]))
删除缺失值最多的列
data.drop(data.isnull().sum().idxmax(),axis=1)
axis=0: 删除行; axis=1: 删除列
data.drop(data.count(axis='index').idxmin(),axis=1,inplace=True)
data.count(axis='index'): 直接按列得到非缺失值的个数
inplace=True参数用于直接修改原始数据
线性代数
标量
标量(scalar): 仅包含一个数值的量
变量(variable):未知的标量值
标量由只有一个元素的张量表示

加法、乘法、除法和指数运算
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x**y
向量
向量:可以被视为标量值组成的列表
元素(element)/分量(component):组成向量的标量值
x = torch.arange(4)
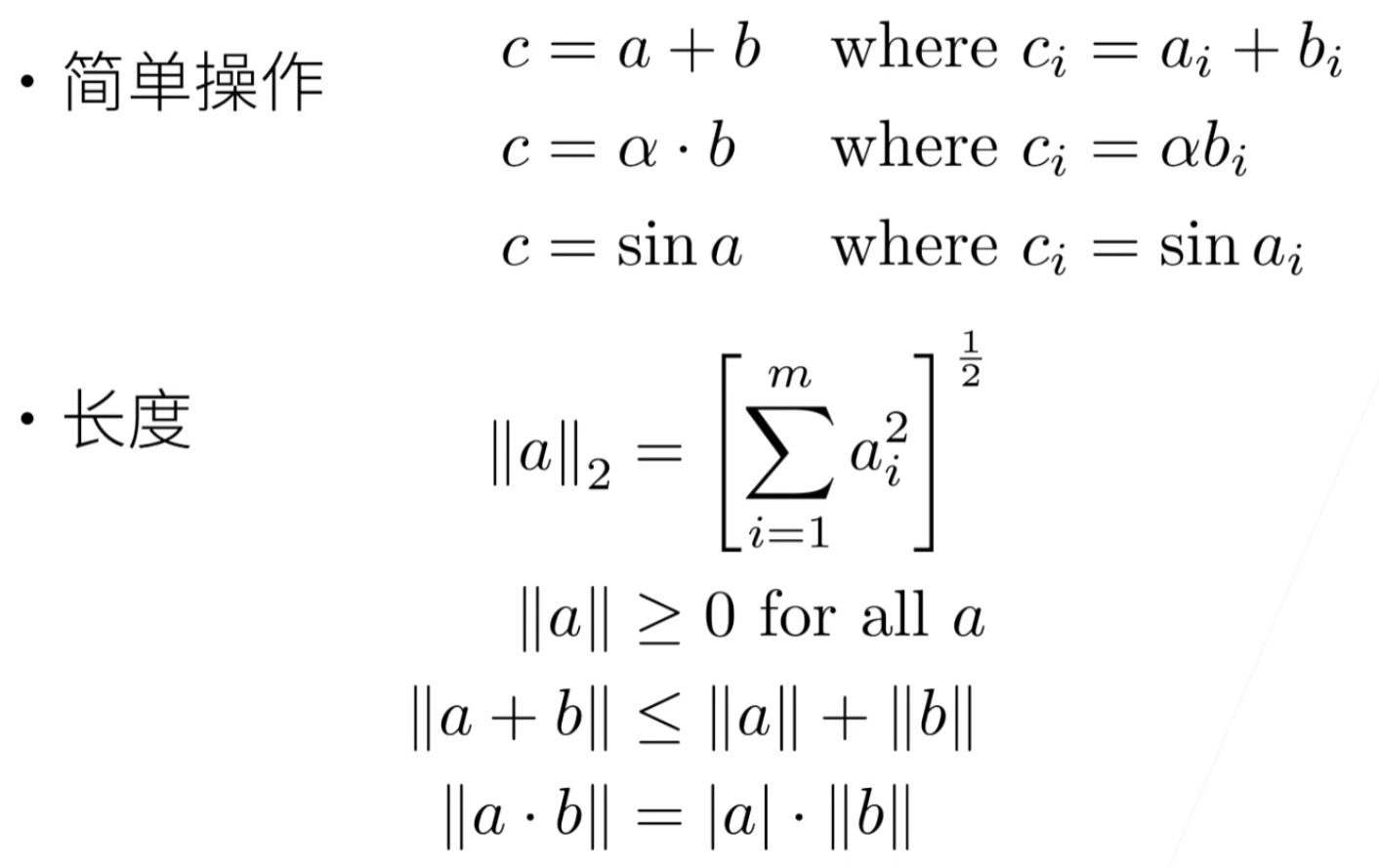
向量的长度
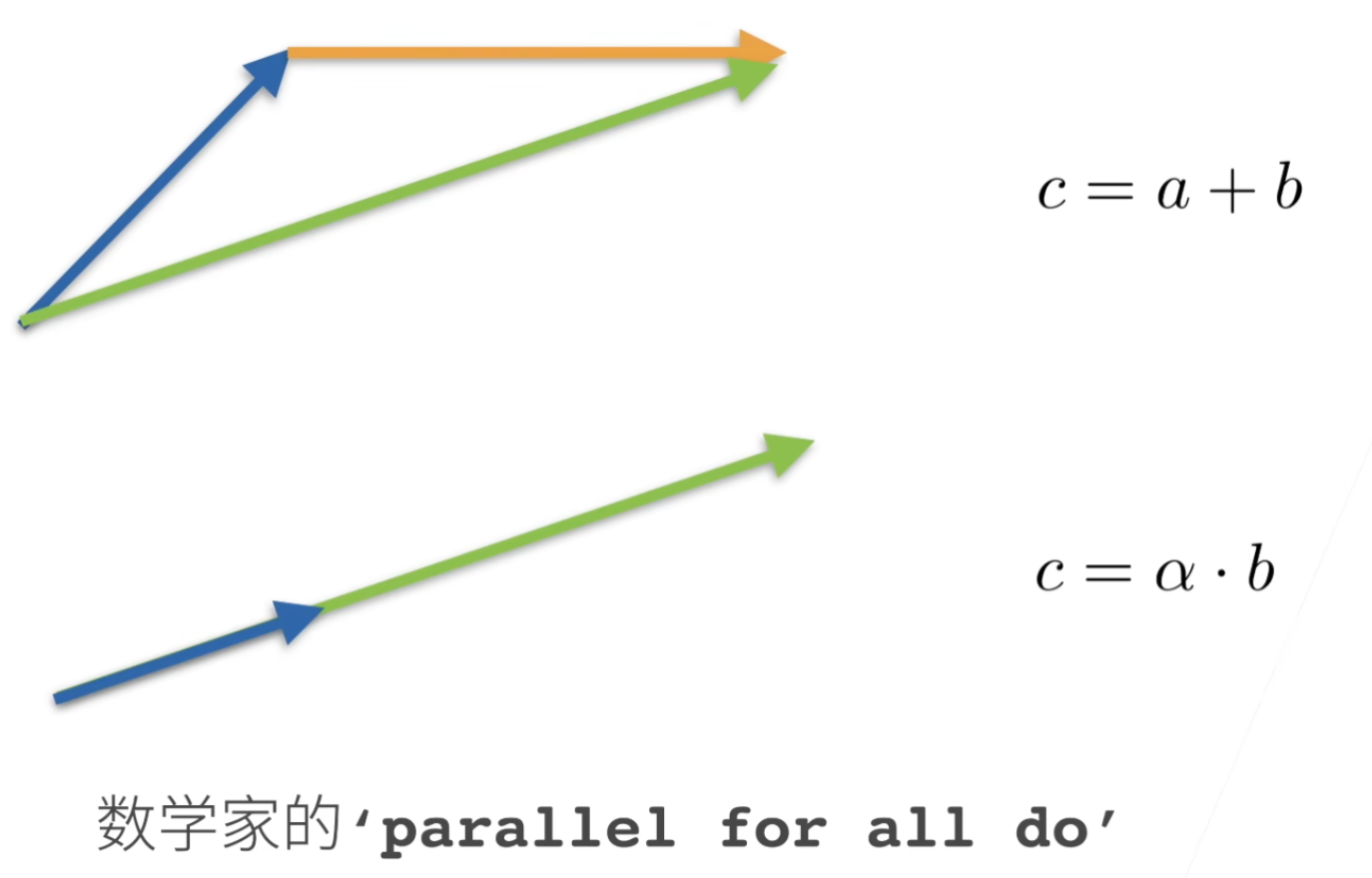
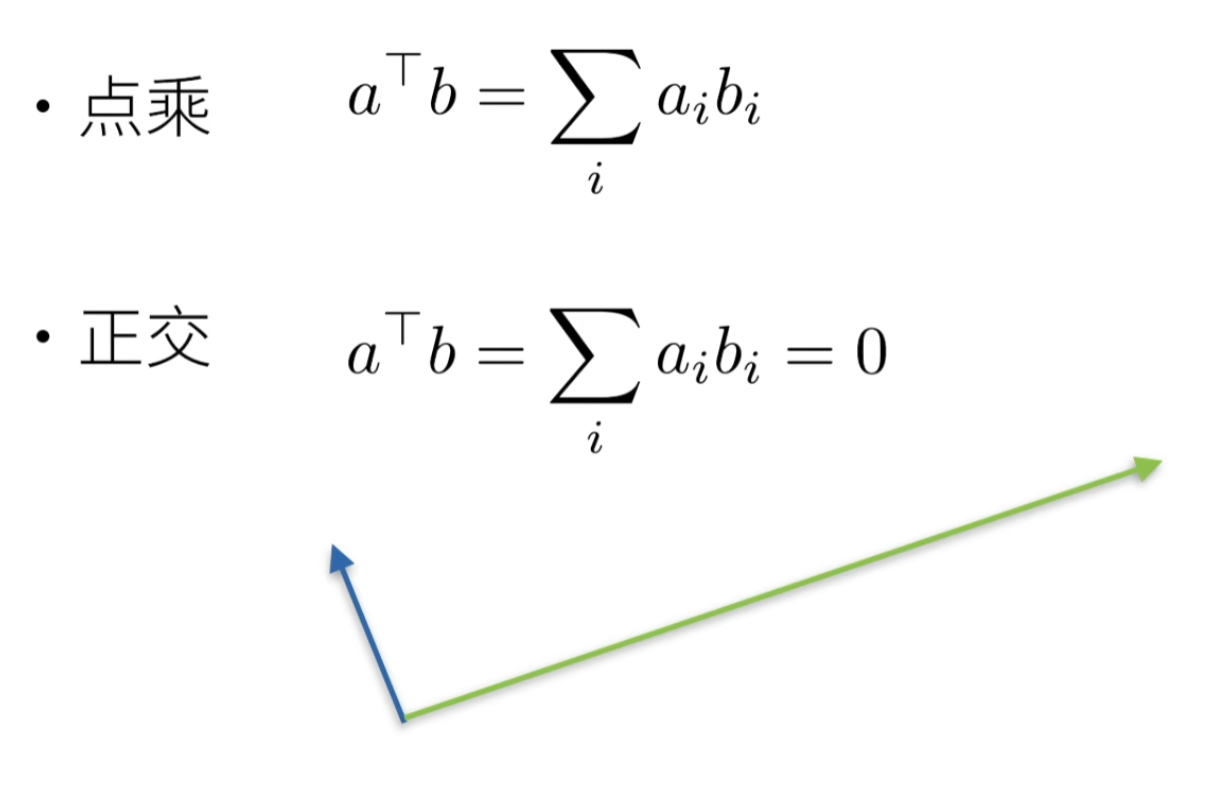
长度、维度和形状
维度(dimension):向量的长度,len()函数来访问张量的长度。
当用张量表示一个向量(只有一个轴)时,我们也可以通过.shape属性访问向量的长度。
维度(dimension)的不同含义:
- 向量或轴的维度被用来表示向量或轴的长度,即向量或轴的元素数量。
- 张量的维度用来表示张量具有的轴数。张量的某个轴的维数就是这个轴的长度。
矩阵
方阵(square matrix):具有相同数量的行和列的矩阵
转置(transpose):交换矩阵行和列的结果通,常用
a
⊤
\mathbf{a}^\top
a⊤来表示,代码A.T
A = torch.arange(20).reshape(5, 4)

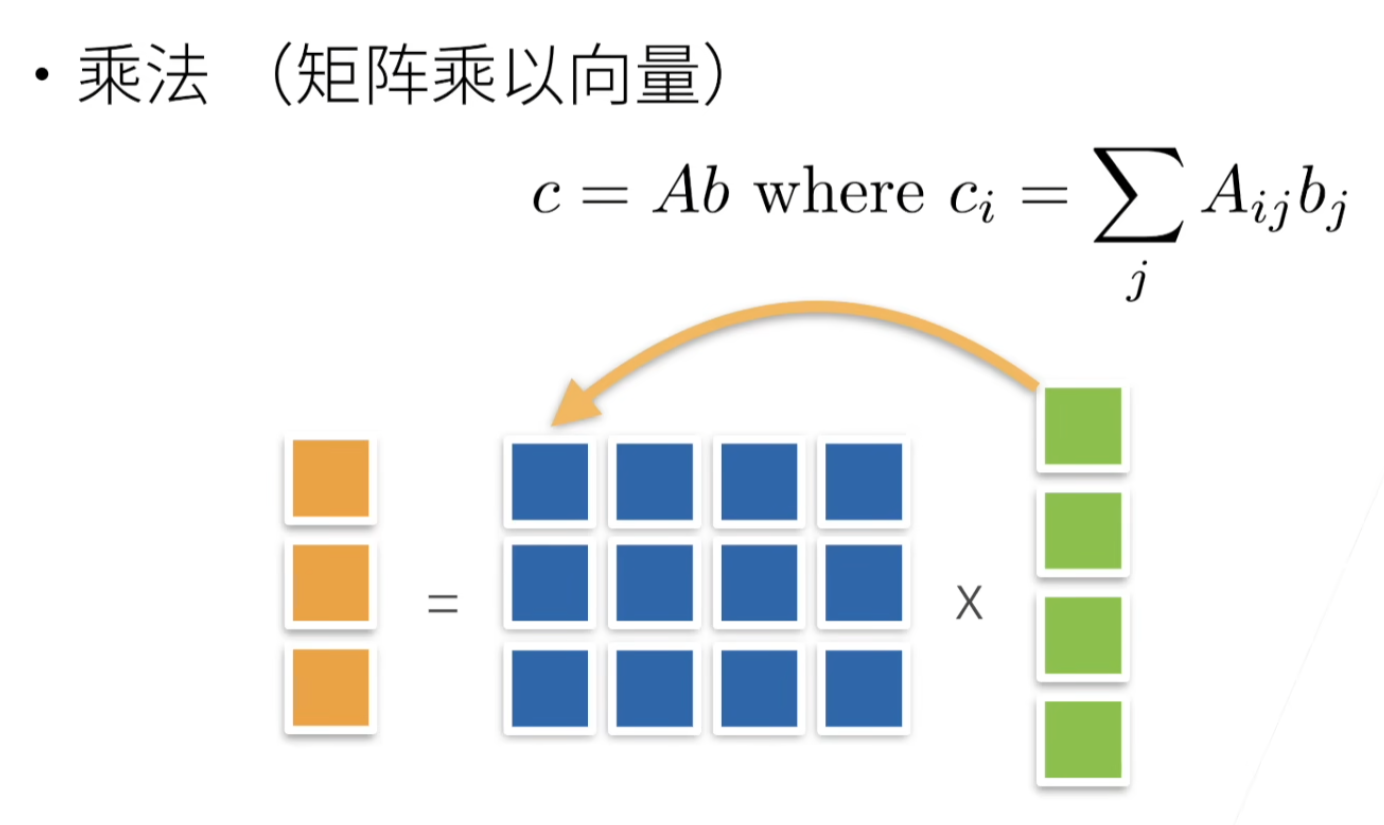
每一行 × 一列向量
直观上:空间的扭曲
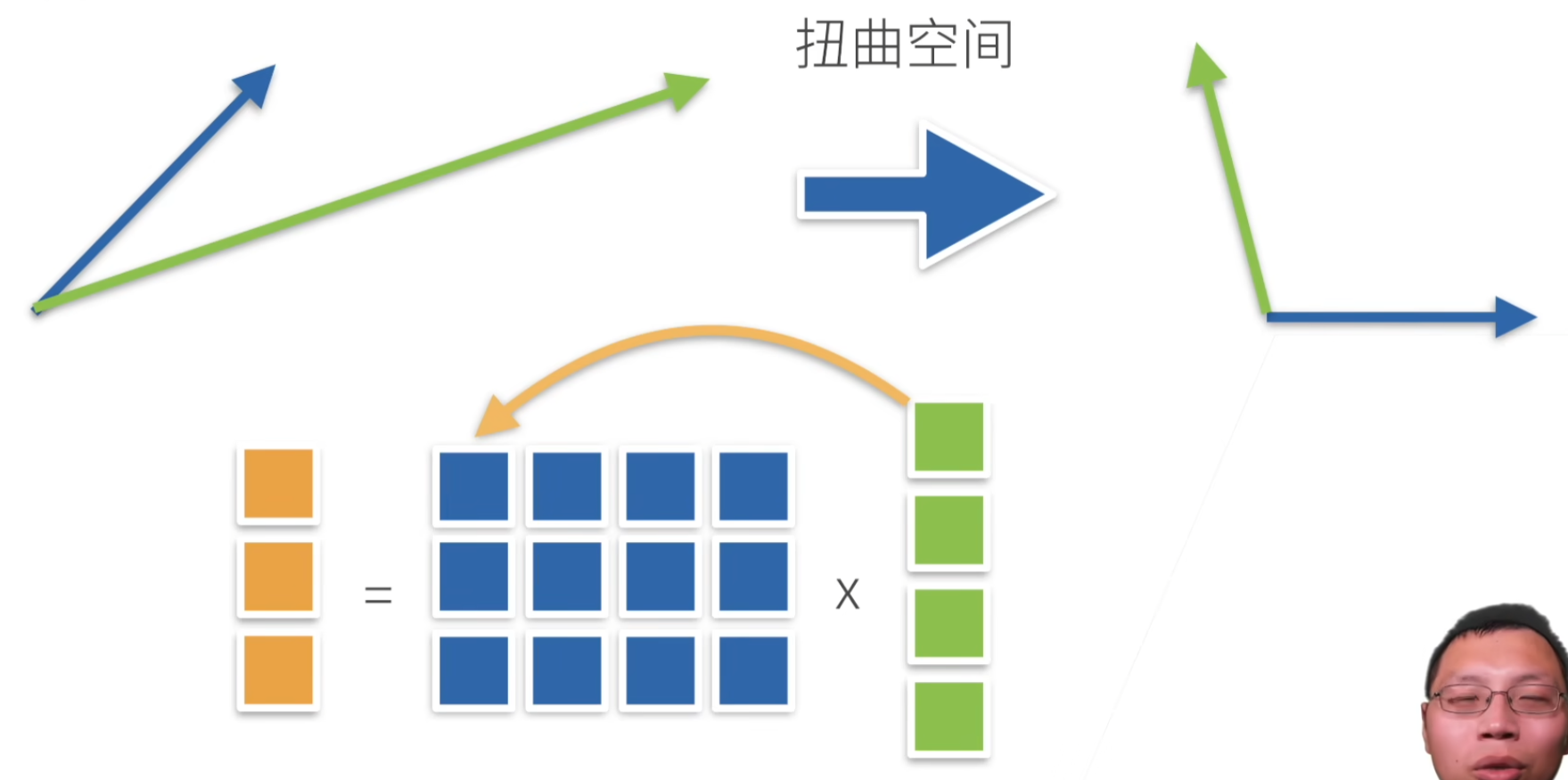
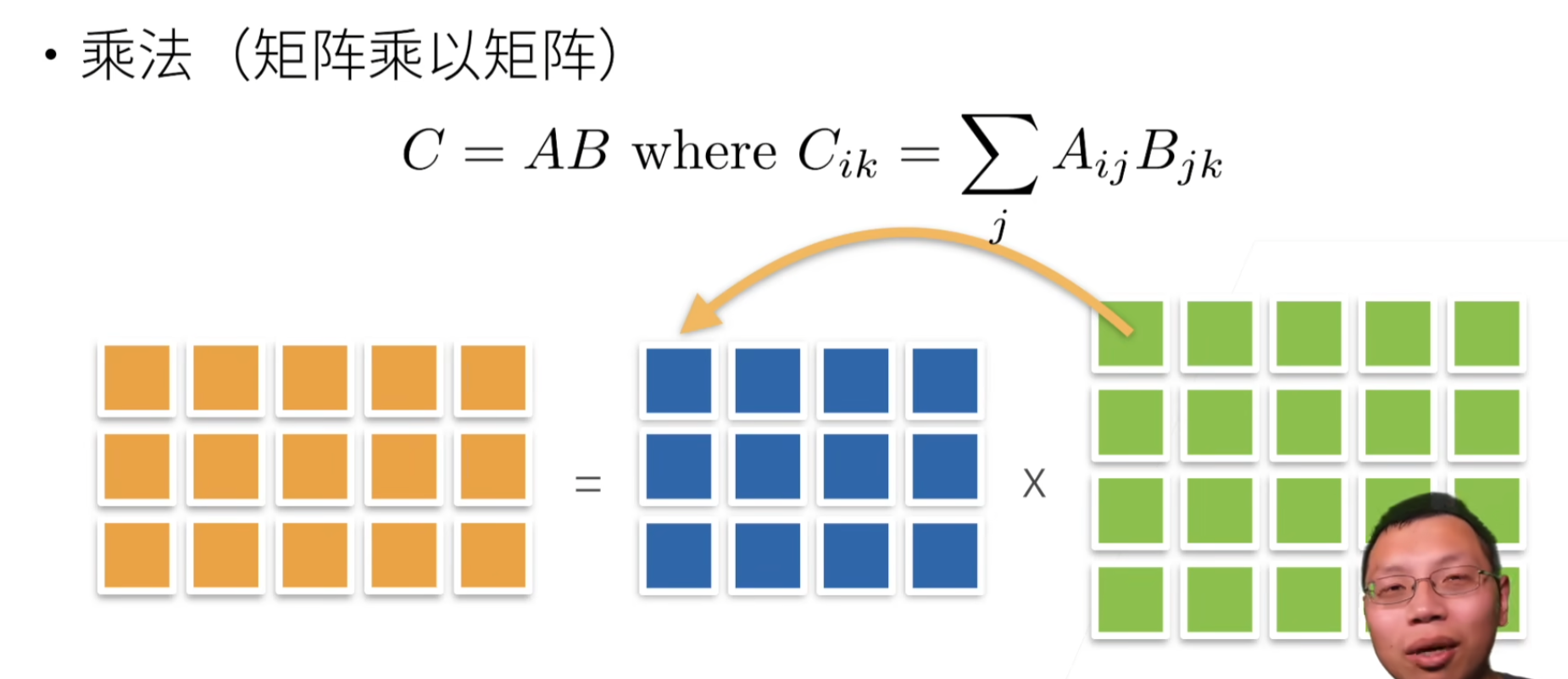
范数

特殊矩阵
对称矩阵(symmetric matrix): A \mathbf{A} A等于其转置: A = A ⊤ \mathbf{A} = \mathbf{A}^\top A=A⊤
正定:正定矩阵乘任何一个列/行向量都 >= 0
- 矩阵是对称的。
- 所有的特征值都是正的。
- 矩阵的所有顶点子矩阵的行列式都是正的。
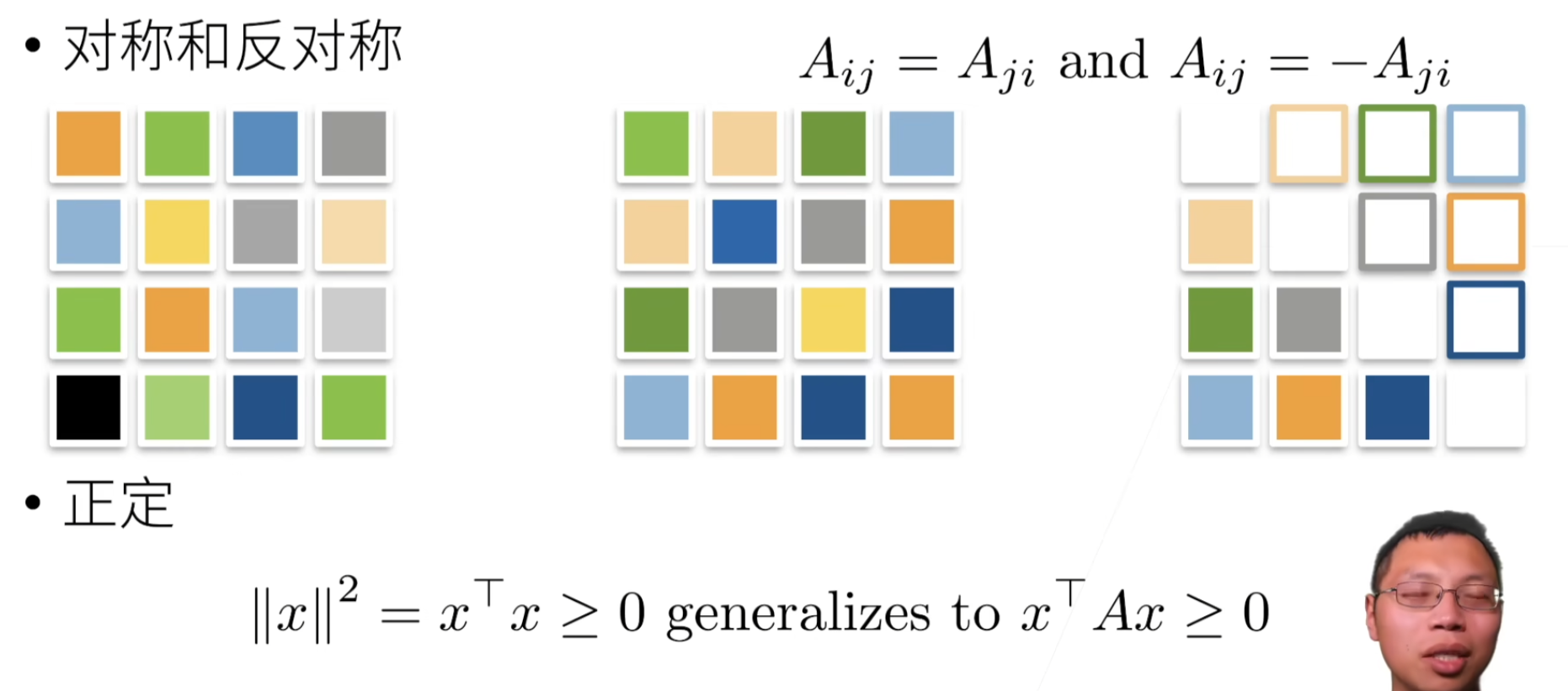

特征向量和特征值
特征向量:不被矩阵改变方向的向量
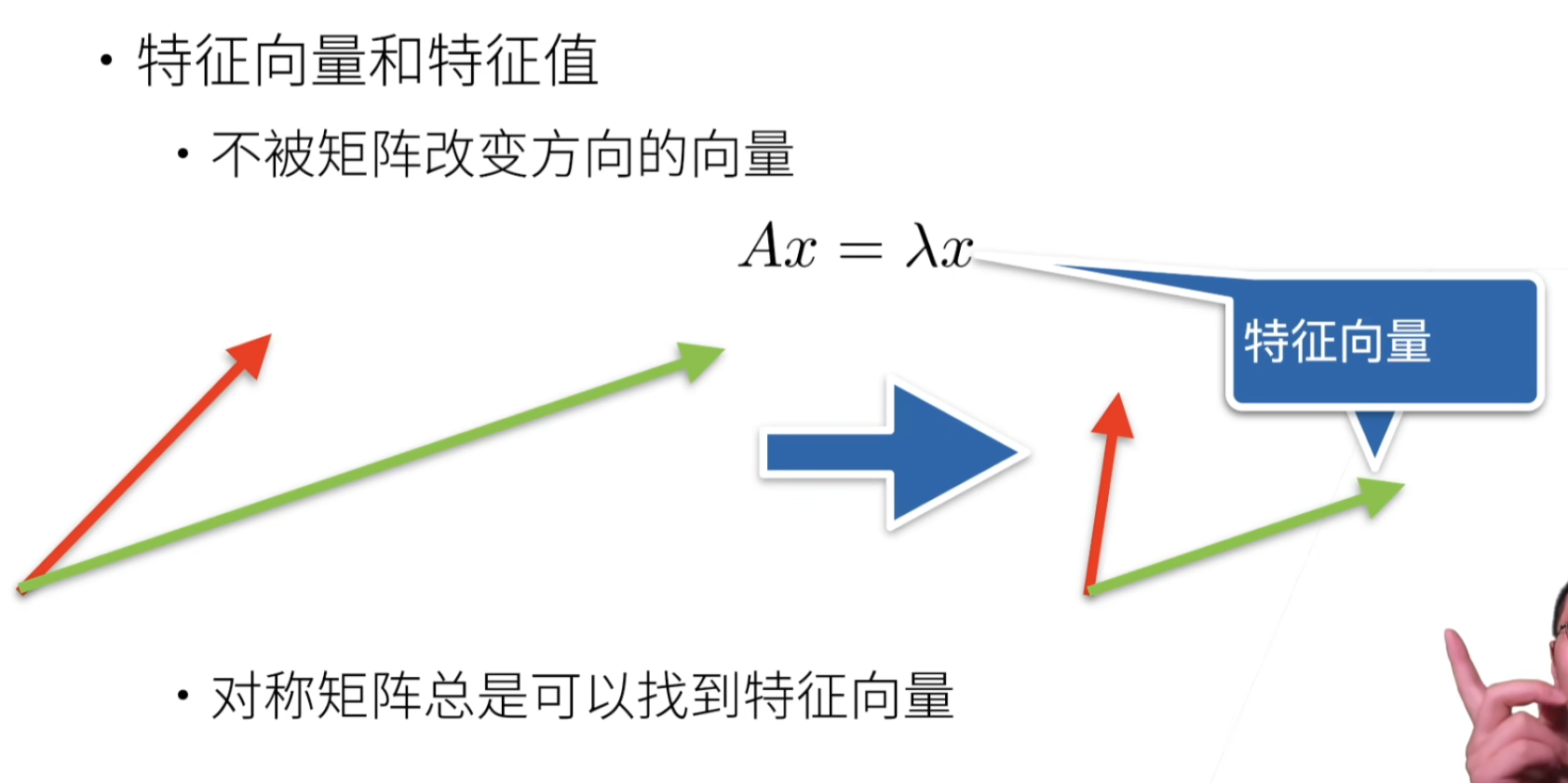
张量
向量是标量的推广,矩阵是向量的推广
张量(本小节中的“张量”指代数对象)是描述具有任意数量轴的𝑛维数组的通用方法。 例如,向量是一阶张量,矩阵是二阶张量。
图像张量:图像以𝑛维数组形式出现, 其中3个轴对应于高度、宽度,以及一个通道(channel)轴, 用于表示颜色通道(红色、绿色和蓝色)。
X = torch.arange(24).reshape(2, 3, 4)
给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量
两个矩阵的按元素乘法称为Hadamard积(Hadamard product)(数学符号⊙)
A
⊙
B
=
[
a
11
b
11
a
12
b
12
…
a
1
n
b
1
n
a
21
b
21
a
22
b
22
…
a
2
n
b
2
n
⋮
⋮
⋱
⋮
a
m
1
b
m
1
a
m
2
b
m
2
…
a
m
n
b
m
n
]
.
\mathbf{A} \odot \mathbf{B} = \begin{bmatrix} a_{11} b_{11} & a_{12} b_{12} & \dots & a_{1n} b_{1n} \\ a_{21} b_{21} & a_{22} b_{22} & \dots & a_{2n} b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} b_{m1} & a_{m2} b_{m2} & \dots & a_{mn} b_{mn} \end{bmatrix}.
A⊙B=
a11b11a21b21⋮am1bm1a12b12a22b22⋮am2bm2……⋱…a1nb1na2nb2n⋮amnbmn
.
A * B
降维
计算张量元素的和
数学表示法使用
∑
\sum
∑符号表示求和。
为了表示长度为
d
d
d的向量中元素的总和,可以记为
∑
i
=
1
d
x
i
\sum_{i=1}^dx_i
∑i=1dxi。
torch.arange(4, dtype=torch.float32).sum()
调用求和函数会沿所有的轴降低张量的维度,使它变为一个标量。
矩阵 A \mathbf{A} A中元素的和可以记为 ∑ i = 1 m ∑ j = 1 n a i j \sum_{i=1}^{m} \sum_{j=1}^{n} a_{ij} ∑i=1m∑j=1naij。
矩阵为例,为了通过求和所有行的元素来降维(轴0),可以在调用函数时指定axis=0。
A.sum(axis=0)
沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和。
A.sum(axis=[0, 1]) # 结果和A.sum()相同
平均值(mean或average):
A.mean(), A.sum() / A.numel()
平均值的函数沿指定轴降低张量的维度
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
非降维求和
keepdims=True作用:保持原数组的维度,方便后续广播
A.sum(axis=1, keepdims=True)计算总和或均值时保持轴数不变
A / sum_A
cumsum函数:沿某个轴计算A元素的累积总和,此函数不会沿任何轴降低输入张量的维度。
点积(Dot Product)——标量
给定两个向量
x
,
y
∈
R
d
\mathbf{x},\mathbf{y}\in\mathbb{R}^d
x,y∈Rd,
点积(dot product)
x
⊤
y
\mathbf{x}^\top\mathbf{y}
x⊤y(或
⟨
x
,
y
⟩
\langle\mathbf{x},\mathbf{y}\rangle
⟨x,y⟩):
相同位置的按元素乘积的和: x ⊤ y = ∑ i = 1 d x i y i \mathbf{x}^\top \mathbf{y} = \sum_{i=1}^{d} x_i y_i x⊤y=∑i=1dxiyi。
torch.dot(x, y)
可以通过执行按元素乘法,然后进行求和来表示两个向量的点积
torch.sum(x * y)
矩阵-向量积
A x = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] x = [ a 1 ⊤ x a 2 ⊤ x ⋮ a m ⊤ x ] . \mathbf{A}\mathbf{x} = \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_m \\ \end{bmatrix}\mathbf{x} = \begin{bmatrix} \mathbf{a}^\top_{1} \mathbf{x} \\ \mathbf{a}^\top_{2} \mathbf{x} \\ \vdots\\ \mathbf{a}^\top_{m} \mathbf{x}\\ \end{bmatrix}. Ax= a1⊤a2⊤⋮am⊤ x= a1⊤xa2⊤x⋮am⊤x .
torch.mv(A, x)
矩阵-矩阵乘法
C = A B = [ a 1 ⊤ a 2 ⊤ ⋮ a n ⊤ ] [ b 1 b 2 ⋯ b m ] = [ a 1 ⊤ b 1 a 1 ⊤ b 2 ⋯ a 1 ⊤ b m a 2 ⊤ b 1 a 2 ⊤ b 2 ⋯ a 2 ⊤ b m ⋮ ⋮ ⋱ ⋮ a n ⊤ b 1 a n ⊤ b 2 ⋯ a n ⊤ b m ] \mathbf{C} = \mathbf{AB} = \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_n \\ \end{bmatrix} \begin{bmatrix} \mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{m} \\ \end{bmatrix} = \begin{bmatrix} \mathbf{a}^\top_{1} \mathbf{b}_1 & \mathbf{a}^\top_{1}\mathbf{b}_2& \cdots & \mathbf{a}^\top_{1} \mathbf{b}_m \\ \mathbf{a}^\top_{2}\mathbf{b}_1 & \mathbf{a}^\top_{2} \mathbf{b}_2 & \cdots & \mathbf{a}^\top_{2} \mathbf{b}_m \\ \vdots & \vdots & \ddots &\vdots\\ \mathbf{a}^\top_{n} \mathbf{b}_1 & \mathbf{a}^\top_{n}\mathbf{b}_2& \cdots& \mathbf{a}^\top_{n} \mathbf{b}_m \end{bmatrix} C=AB= a1⊤a2⊤⋮an⊤ [b1b2⋯bm]= a1⊤b1a2⊤b1⋮an⊤b1a1⊤b2a2⊤b2⋮an⊤b2⋯⋯⋱⋯a1⊤bma2⊤bm⋮an⊤bm
torch.mm(A, B)
范数
向量的范数是表示一个向量的长度。
L
2
L_2
L2范数(常用):
∥
x
∥
2
=
∑
i
=
1
n
x
i
2
\|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2}
∥x∥2=i=1∑nxi2
常常省略下标
2
2
2,也就是说
∥
x
∥
\|\mathbf{x}\|
∥x∥等同于
∥
x
∥
2
\|\mathbf{x}\|_2
∥x∥2。
torch.norm(u)
L
1
L_1
L1范数:向量元素的绝对值之和
∥
x
∥
1
=
∑
i
=
1
n
∣
x
i
∣
\|\mathbf{x}\|_1 = \sum_{i=1}^n \left|x_i \right|
∥x∥1=i=1∑n∣xi∣
torch.abs(u).sum()
L
p
L_p
Lp范数
∥
x
∥
p
=
(
∑
i
=
1
n
∣
x
i
∣
p
)
1
/
p
\|\mathbf{x}\|_p = \left(\sum_{i=1}^n \left|x_i \right|^p \right)^{1/p}
∥x∥p=(i=1∑n∣xi∣p)1/p
Frobenius范数(Frobenius norm):是矩阵元素平方和的平方根
∥
X
∥
F
=
∑
i
=
1
m
∑
j
=
1
n
x
i
j
2
\|\mathbf{X}\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n x_{ij}^2}
∥X∥F=i=1∑mj=1∑nxij2
torch.norm(A)
目标通常被表达为范数
PS:torch.norm() 函数期望接收一个浮点型或复数型的张量作为输入
微积分
积分(integral calculus)
微分(differential calculus)
拟合模型:
- 优化(optimization):用模型拟合观测数据的过程;
- 泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型。
导数和微分
如果 f f f的导数存在,这个极限被定义为
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}
f′(x)=h→0limhf(x+h)−f(x)
如果
f
′
(
a
)
f'(a)
f′(a)存在,则称
f
f
f在
a
a
a处是可微(differentiable)的。
如果
f
f
f在一个区间内的每个数上都是可微的,则此函数在此区间中是可微的。
f
′
(
x
)
f'(x)
f′(x)为
f
(
x
)
f(x)
f(x)相对于
x
x
x的瞬时(instantaneous)变化率。
f
′
(
x
)
=
y
′
=
d
y
d
x
=
d
f
d
x
=
d
d
x
f
(
x
)
=
D
f
(
x
)
=
D
x
f
(
x
)
f'(x) = y' = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx} f(x) = Df(x) = D_x f(x)
f′(x)=y′=dxdy=dxdf=dxdf(x)=Df(x)=Dxf(x)
符号
d
d
x
\frac{d}{dx}
dxd和
D
D
D是微分运算符,表示微分操作。
- D C = 0 DC = 0 DC=0( C C C是一个常数)
- D x n = n x n − 1 Dx^n = nx^{n-1} Dxn=nxn−1(幂律(power rule), n n n是任意实数)
- D e x = e x De^x = e^x Dex=ex
- D ln ( x ) = 1 / x D\ln(x) = 1/x Dln(x)=1/x
常数相乘法则
d
d
x
[
C
f
(
x
)
]
=
C
d
d
x
f
(
x
)
,
\frac{d}{dx} [Cf(x)] = C \frac{d}{dx} f(x),
dxd[Cf(x)]=Cdxdf(x),
加法法则
d d x [ f ( x ) + g ( x ) ] = d d x f ( x ) + d d x g ( x ) , \frac{d}{dx} [f(x) + g(x)] = \frac{d}{dx} f(x) + \frac{d}{dx} g(x), dxd[f(x)+g(x)]=dxdf(x)+dxdg(x),
乘法法则
d d x [ f ( x ) g ( x ) ] = f ( x ) d d x [ g ( x ) ] + g ( x ) d d x [ f ( x ) ] , \frac{d}{dx} [f(x)g(x)] = f(x) \frac{d}{dx} [g(x)] + g(x) \frac{d}{dx} [f(x)], dxd[f(x)g(x)]=f(x)dxd[g(x)]+g(x)dxd[f(x)],
除法法则
d d x [ f ( x ) g ( x ) ] = g ( x ) d d x [ f ( x ) ] − f ( x ) d d x [ g ( x ) ] [ g ( x ) ] 2 . \frac{d}{dx} \left[\frac{f(x)}{g(x)}\right] = \frac{g(x) \frac{d}{dx} [f(x)] - f(x) \frac{d}{dx} [g(x)]}{[g(x)]^2}. dxd[g(x)f(x)]=[g(x)]2g(x)dxd[f(x)]−f(x)dxd[g(x)].
注释#@save是一个特殊的标记,会将对应的函数、类或语句保存在d2l包中。

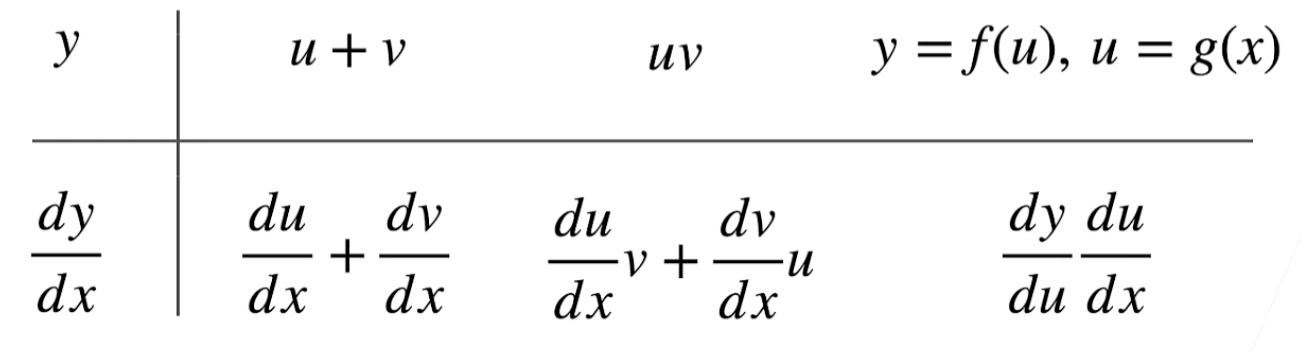
亚倒数

偏导数
设
y
=
f
(
x
1
,
x
2
,
…
,
x
n
)
y = f(x_1, x_2, \ldots, x_n)
y=f(x1,x2,…,xn)是一个具有
n
n
n个变量的函数。
y
y
y关于第
i
i
i个参数
x
i
x_i
xi的偏导数(partial derivative)为:
∂
y
∂
x
i
=
lim
h
→
0
f
(
x
1
,
…
,
x
i
−
1
,
x
i
+
h
,
x
i
+
1
,
…
,
x
n
)
−
f
(
x
1
,
…
,
x
i
,
…
,
x
n
)
h
\frac{\partial y}{\partial x_i} = \lim_{h \rightarrow 0} \frac{f(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots, x_n) - f(x_1, \ldots, x_i, \ldots, x_n)}{h}
∂xi∂y=h→0limhf(x1,…,xi−1,xi+h,xi+1,…,xn)−f(x1,…,xi,…,xn)
将
x
1
,
…
,
x
i
−
1
,
x
i
+
1
,
…
,
x
n
x_1, \ldots, x_{i-1}, x_{i+1}, \ldots, x_n
x1,…,xi−1,xi+1,…,xn看作常数,计算
y
y
y关于
x
i
x_i
xi的导数。
∂
y
∂
x
i
=
∂
f
∂
x
i
=
f
x
i
=
f
i
=
D
i
f
=
D
x
i
f
\frac{\partial y}{\partial x_i} = \frac{\partial f}{\partial x_i} = f_{x_i} = f_i = D_i f = D_{x_i} f
∂xi∂y=∂xi∂f=fxi=fi=Dif=Dxif
梯度
将导数拓展为向量
连结一个多元函数对其所有变量的偏导数,以得到该函数的梯度(gradient)向量。
∇
x
f
(
x
)
=
[
∂
f
(
x
)
∂
x
1
,
∂
f
(
x
)
∂
x
2
,
…
,
∂
f
(
x
)
∂
x
n
]
⊤
\nabla_{\mathbf{x}} f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_n}\bigg]^\top
∇xf(x)=[∂x1∂f(x),∂x2∂f(x),…,∂xn∂f(x)]⊤
∇
x
f
(
x
)
\nabla_{\mathbf{x}} f(\mathbf{x})
∇xf(x)通常在没有歧义时被
∇
f
(
x
)
\nabla f(\mathbf{x})
∇f(x)取代。
- 对于所有 A ∈ R m × n \mathbf{A} \in \mathbb{R}^{m \times n} A∈Rm×n,都有 ∇ x A x = A ⊤ \nabla_{\mathbf{x}} \mathbf{A} \mathbf{x} = \mathbf{A}^\top ∇xAx=A⊤
- 对于所有 A ∈ R n × m \mathbf{A} \in \mathbb{R}^{n \times m} A∈Rn×m,都有 ∇ x x ⊤ A = A \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A} = \mathbf{A} ∇xx⊤A=A
- 对于所有 A ∈ R n × n \mathbf{A} \in \mathbb{R}^{n \times n} A∈Rn×n,都有 ∇ x x ⊤ A x = ( A + A ⊤ ) x \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A} \mathbf{x} = (\mathbf{A} + \mathbf{A}^\top)\mathbf{x} ∇xx⊤Ax=(A+A⊤)x
- ∇ x ∥ x ∥ 2 = ∇ x x ⊤ x = 2 x \nabla_{\mathbf{x}} \|\mathbf{x} \|^2 = \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{x} = 2\mathbf{x} ∇x∥x∥2=∇xx⊤x=2x
对于任何矩阵 X \mathbf{X} X,都有 ∇ X ∥ X ∥ F 2 = 2 X \nabla_{\mathbf{X}} \|\mathbf{X} \|_F^2 = 2\mathbf{X} ∇X∥X∥F2=2X。
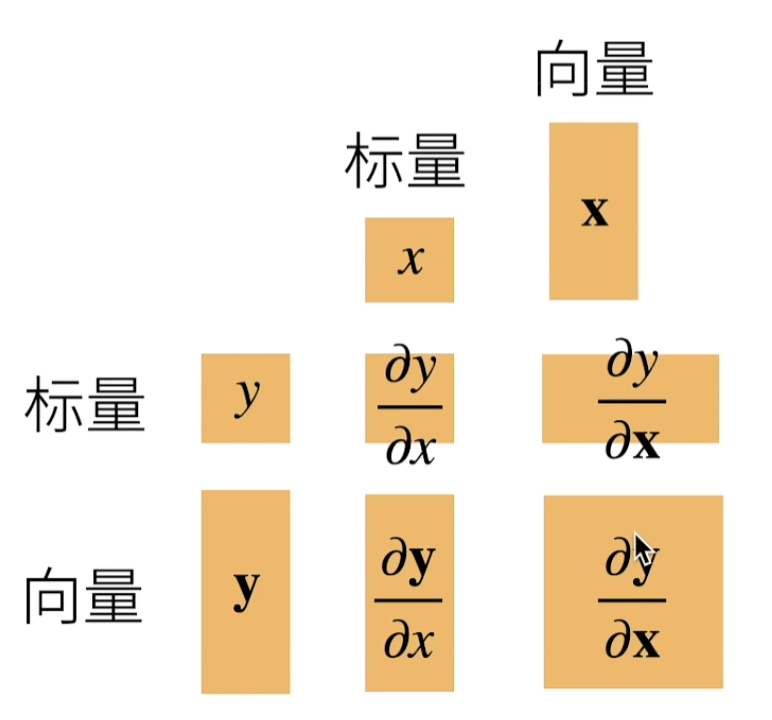
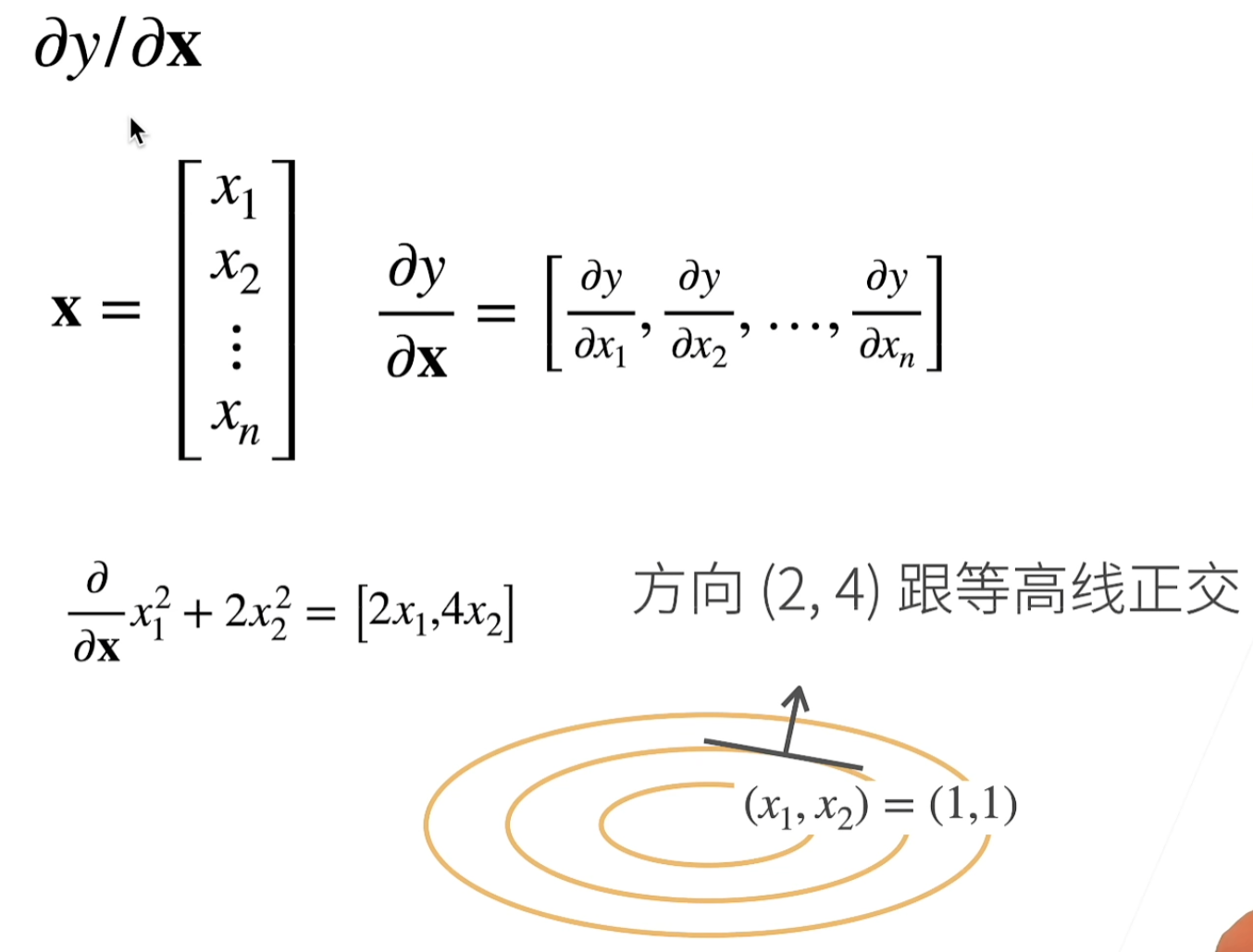
y是标量x是向量
标量关于列向量的导数是行向量
梯度指向值变化最大的方向
a 不是关于 x 的函数
0 and 1 are vectors,全为0/1的向量
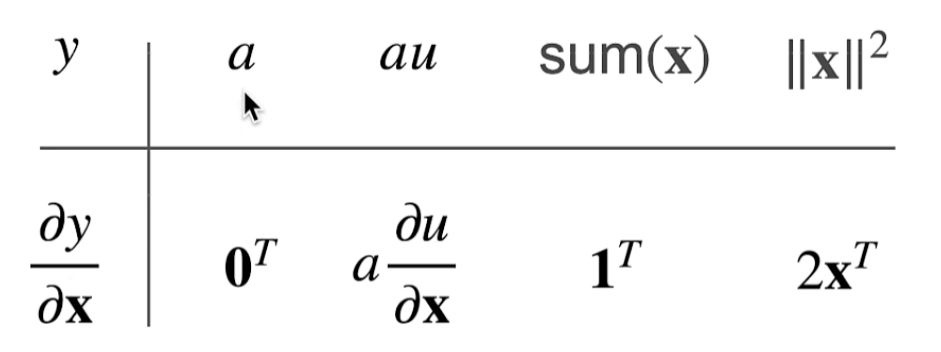
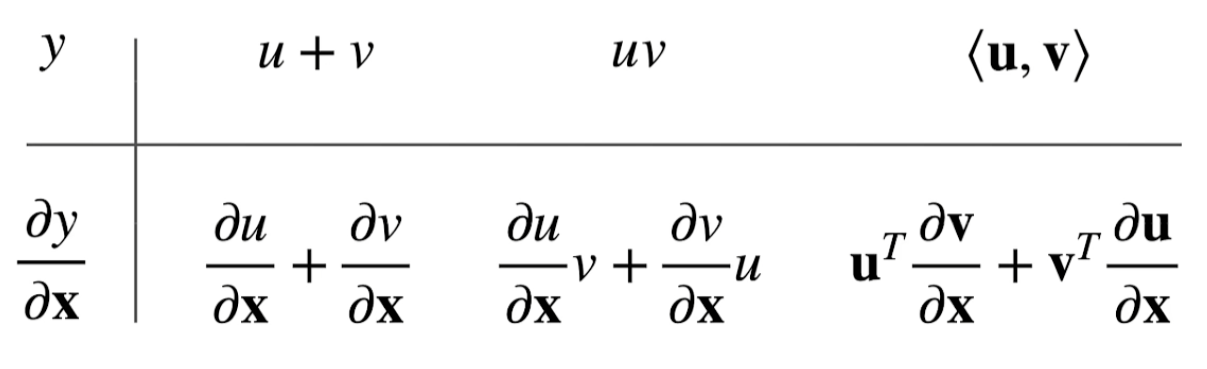
y是向量x是标量

这个被称之为分子布局符号,反过来的版本叫分母布局符号
y是向量x是向量
向量对向量最后是一个矩阵

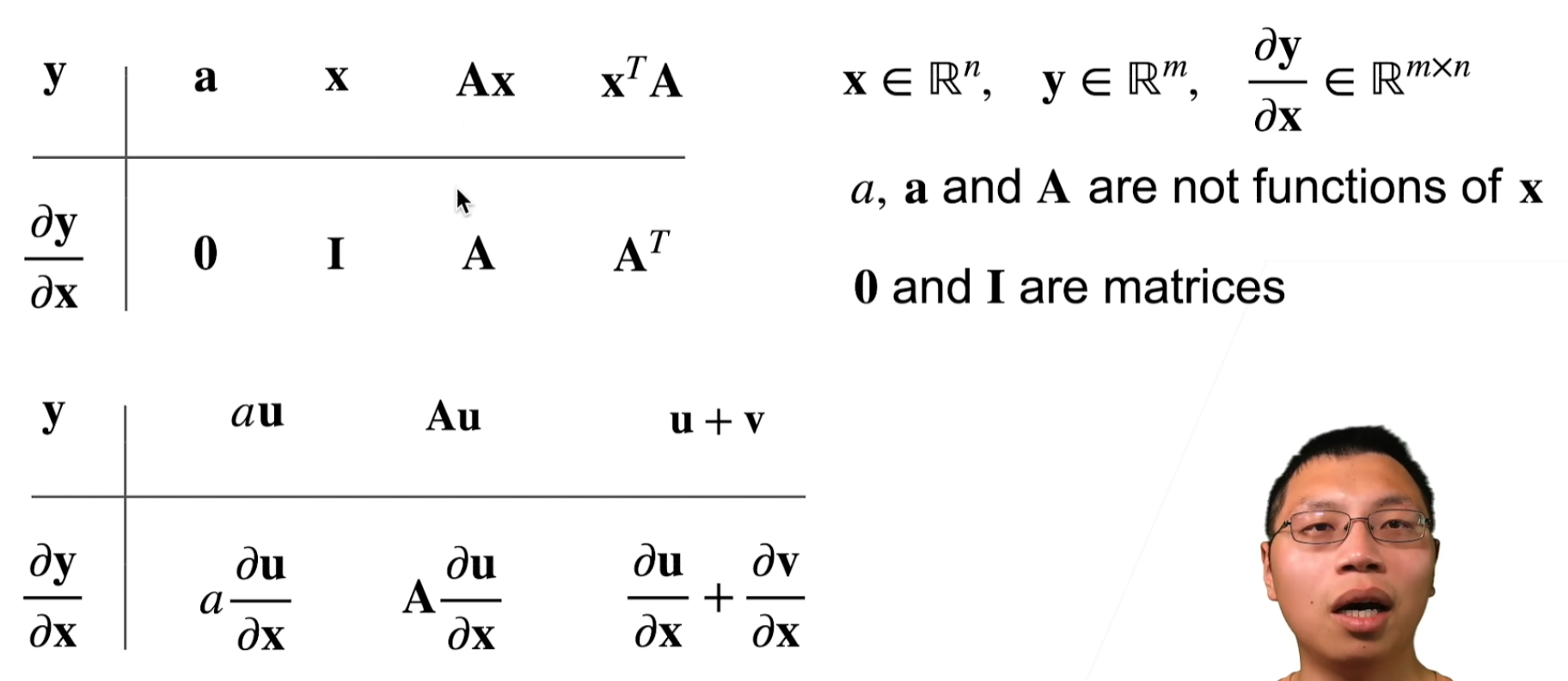
链式法则
∂ y ∂ x i = ∂ y ∂ u 1 ∂ u 1 ∂ x i + ∂ y ∂ u 2 ∂ u 2 ∂ x i + ⋯ + ∂ y ∂ u m ∂ u m ∂ x i \frac{\partial y}{\partial x_i} = \frac{\partial y}{\partial u_1} \frac{\partial u_1}{\partial x_i} + \frac{\partial y}{\partial u_2} \frac{\partial u_2}{\partial x_i} + \cdots + \frac{\partial y}{\partial u_m} \frac{\partial u_m}{\partial x_i} ∂xi∂y=∂u1∂y∂xi∂u1+∂u2∂y∂xi∂u2+⋯+∂um∂y∂xi∂um
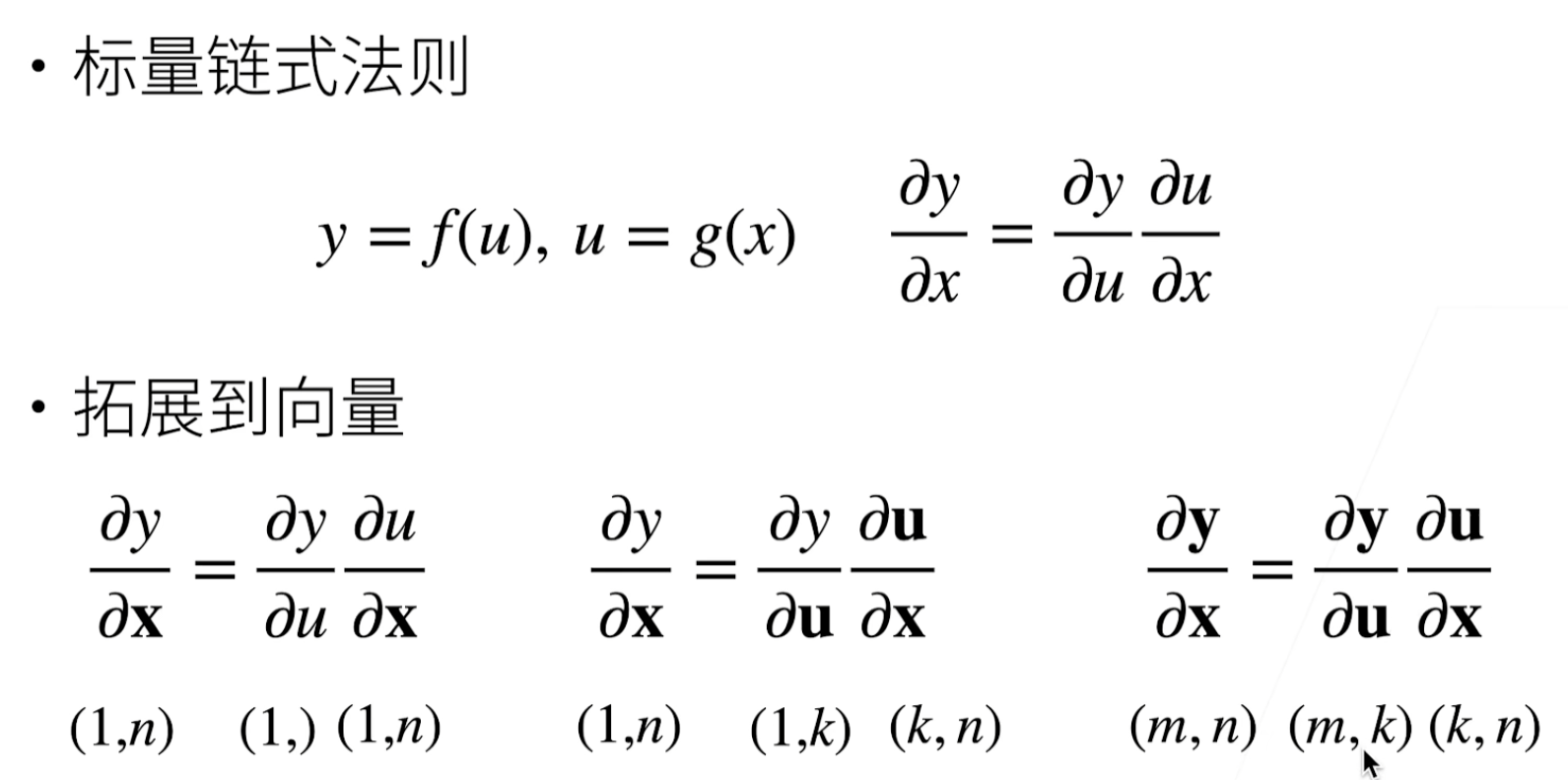
自动求导
深度学习框架可以自动求导:
- 将梯度附加到想要对其计算偏导数的变量
- 记录目标值的计算
- 执行它的反向传播函数
- 访问得到的梯度
自动微分(automatic differentiation):计算一个函数在指定值上的导数
计算图(computational graph):跟踪计算是哪些数据通过哪些操作组合起来产生输出
- 将代码分解成操作子
- 将计算表示成一个无环图
- 显式构造:Tensorflow/Theano/MXNet
- 隐式构造:PyTorch/MXNet
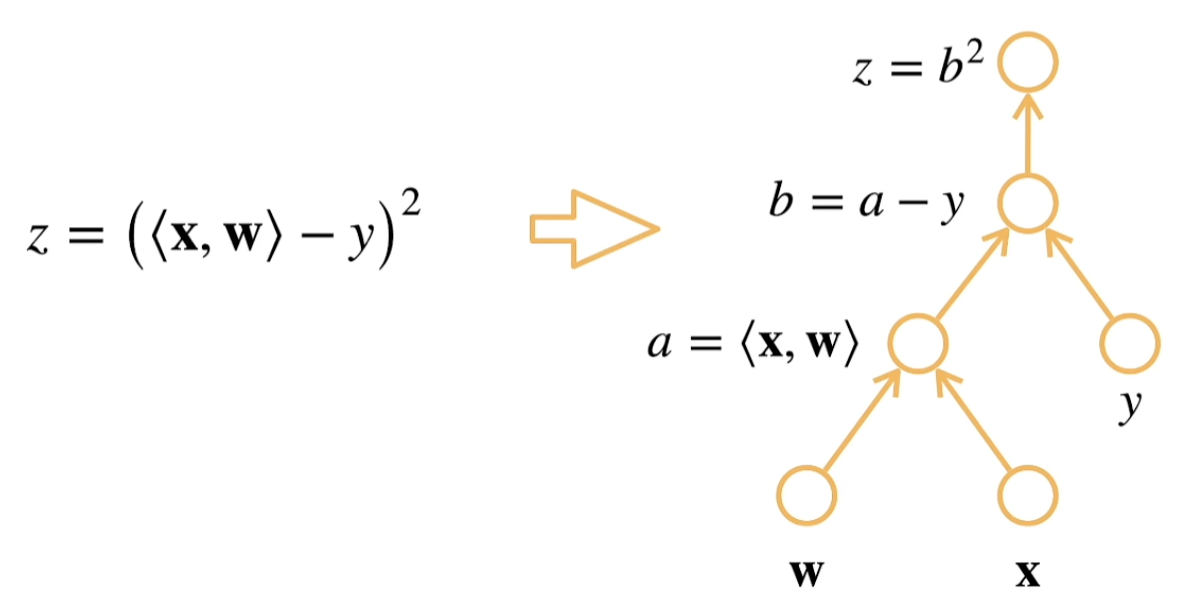
两种模式

反向传播(backpropagate):跟踪整个计算图,填充关于每个参数的偏导数。自动微分使系统能够随后反向传播梯度。
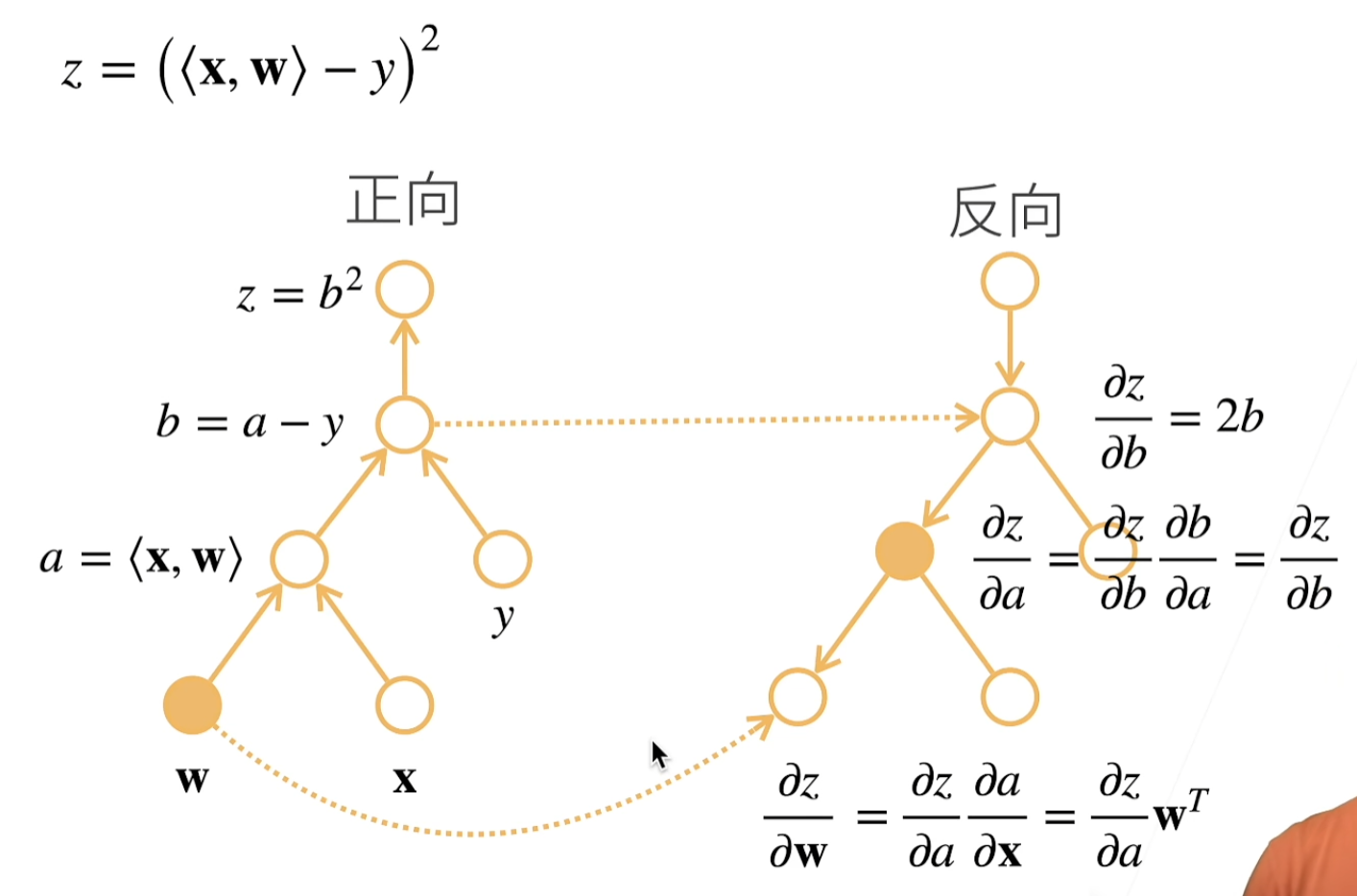
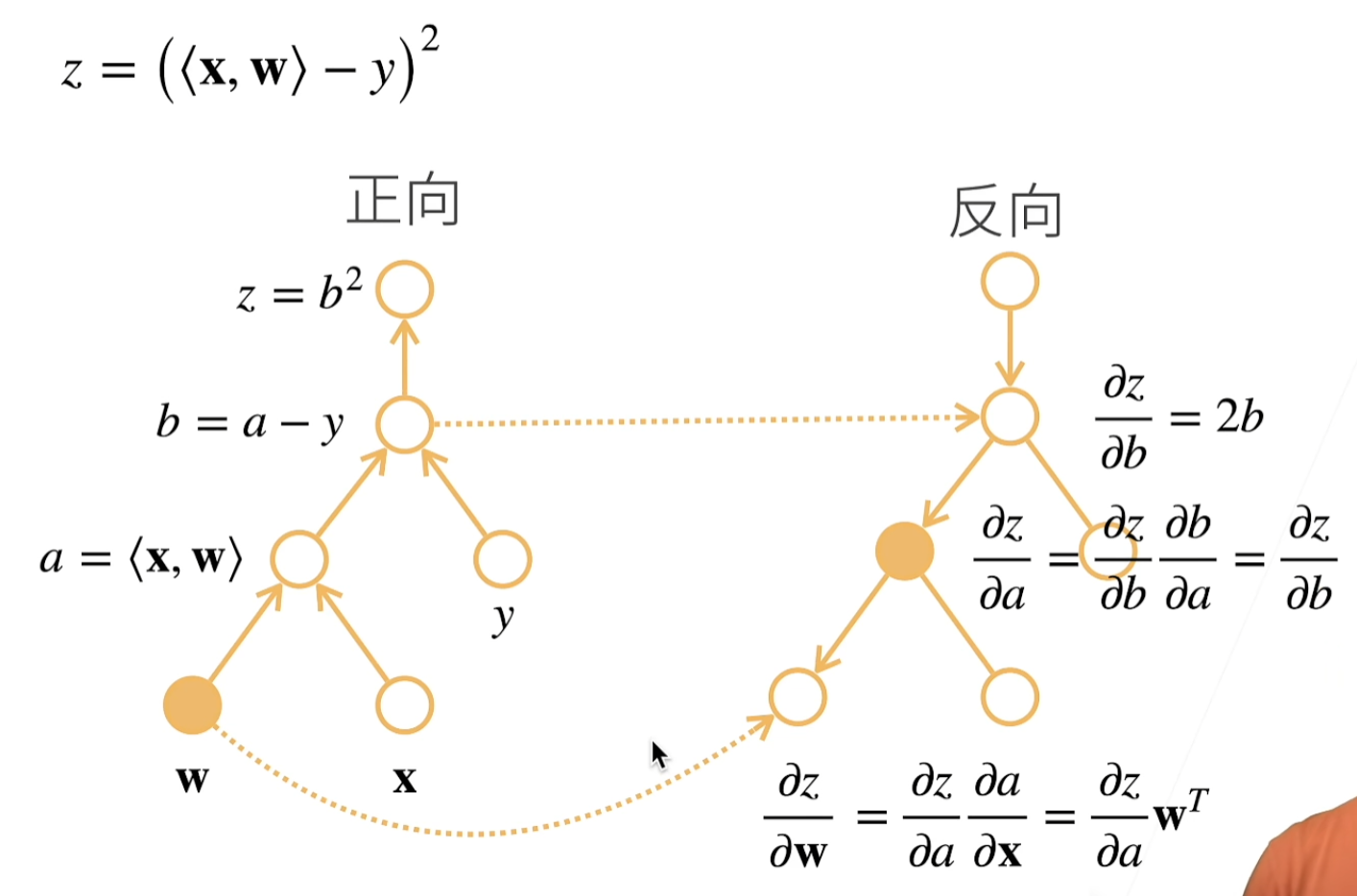
复杂度

一个标量函数关于向量𝐱的梯度是向量,并且与𝐱具有相同的形状。
x.requires_grad_(True)
PyTorch将会开始跟踪在 x 上进行的所有操作,为自动求导(自动微分)建立计算图。
计算反向传播
y.backward()
在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
分离计算
将某些计算移动到记录的计算图之外
y.detach()
Python控制流的梯度计算
即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度
隐式控制
Q:为什么pytorch会默认累计梯度?
A:
- 梯度累积:在某些情况下,你可能希望在多个迷你批次(mini-batches)上累积梯度,然后一起更新权重。这对于处理那些因为内存限制而无法一次性处理的大批次数据很有用。在每个迷你批次上计算梯度并累积可以近似这个大批次的效果。
- 更精细的梯度控制:某些高级训练技巧,如梯度裁剪或者使用不同的梯度更新策略,可能需要在执行实际的参数更新之前访问和修改梯度。累积梯度提供了在更新之前手动检查和修改梯度的机会。
- 节省计算资源:对于某些复杂的模型结构,比如使用了多任务学习的网络,可能需要将梯度从多个任务中累积起来再更新。累积梯度使得只需进行一次权重更新,而不是在每个任务完成后都更新。
- 提高稳定性:在某些情况下,累积梯度可以帮助提高训练过程的稳定性,因为它允许梯度从多个样本中得出,可能会导致更平滑的梯度估计和更新。