【C语言】红黑树详解以及C语言模拟

news2025/1/12 12:22:09

    • 一、红黑树的性质
    • 二、红黑树的旋转操作
    • 三、红黑树的插入操作
    • 四、红黑树的删除操作
    • 五、红黑树的应用
    • 六、C语言模拟红黑树
    • 七、总结

 红黑树是一种自平衡二叉查找树，它能够保持树的平衡，从而确保查找、插入和删除的最坏情况时间复杂度为O( l o g n log_n logn​)。在红黑树中，节点被涂成红色或黑色，并且通过旋转和重新着色等操作来保持树的平衡。本文将详细介绍红黑树的原理，并使用C语言进行模拟实现。

一、红黑树的性质

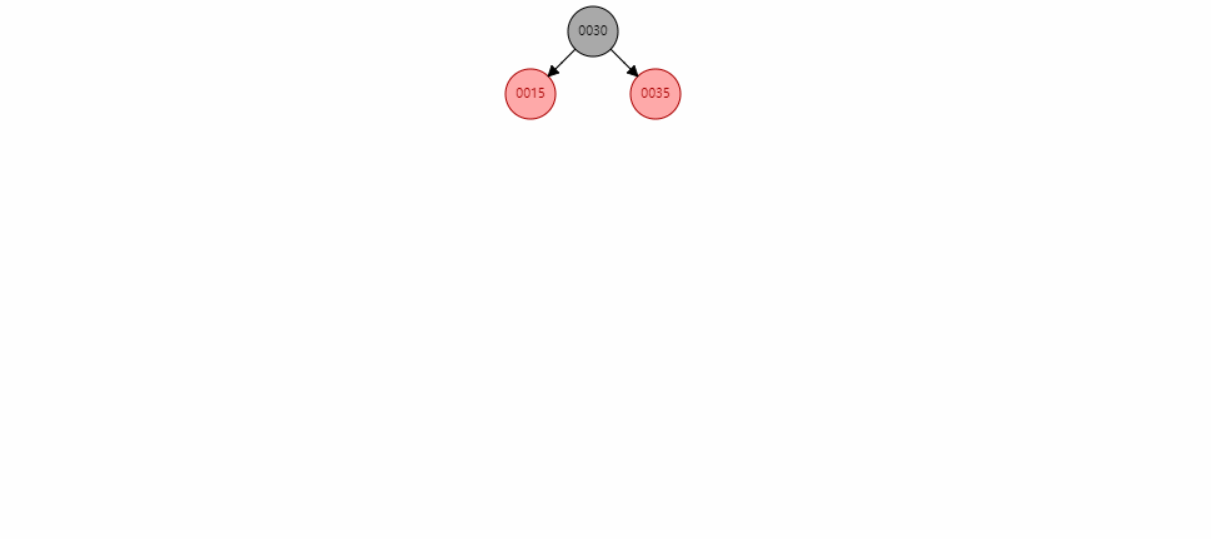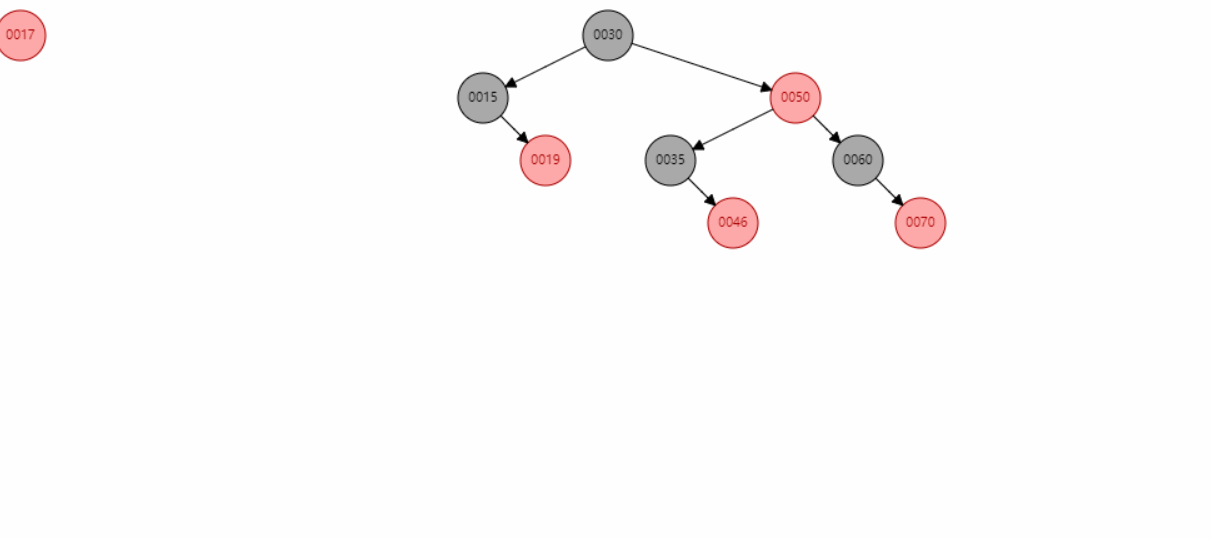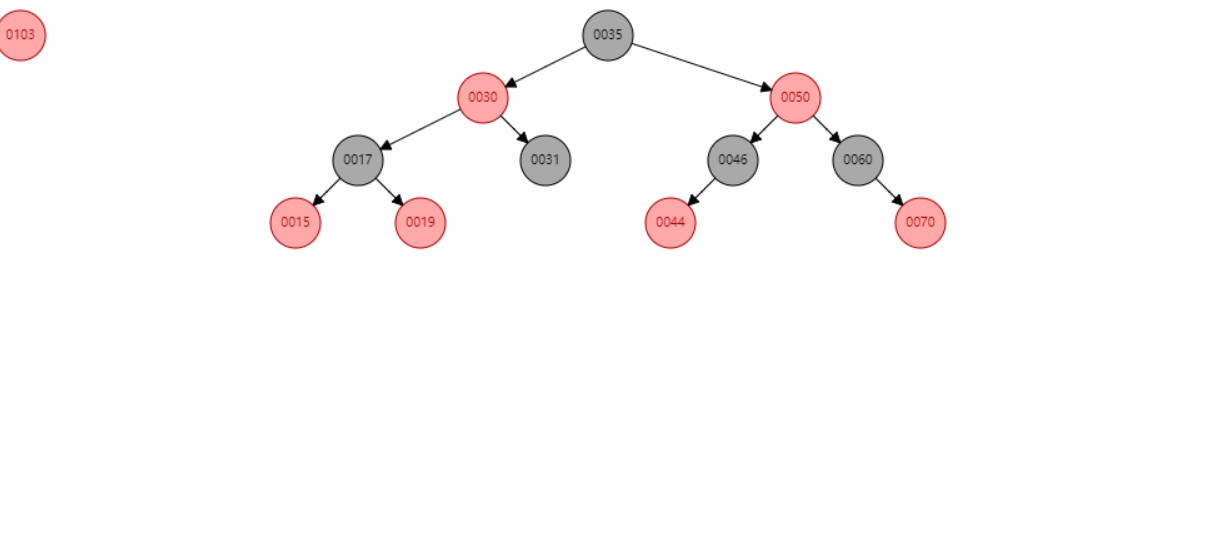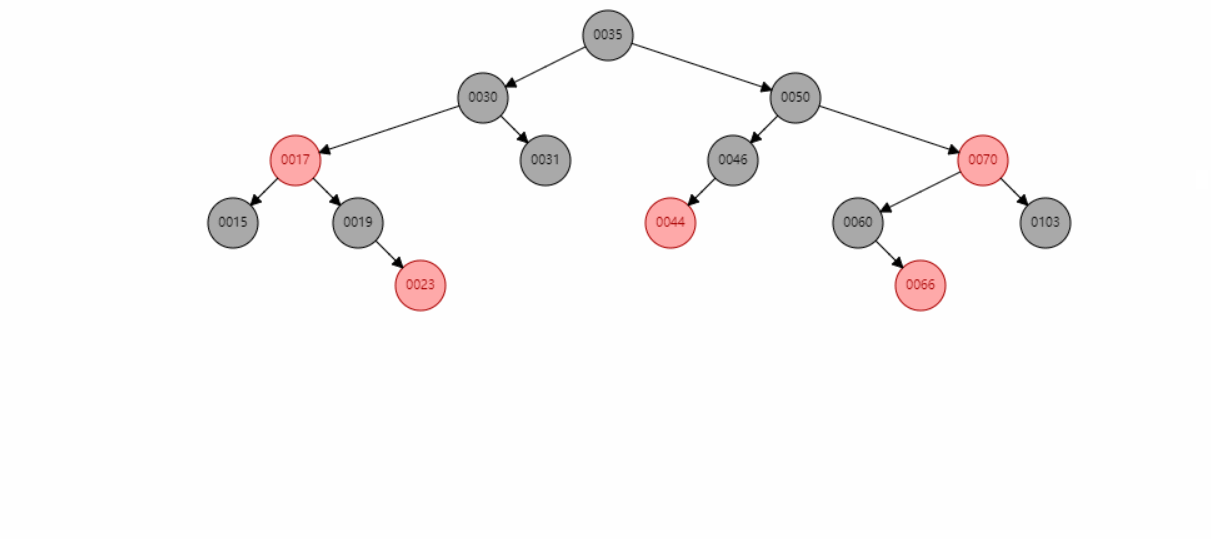
请添加图片描述

红黑树具有以下性质：

  1. 每个节点非红即黑。
  2. 根节点是黑色的。
  3. 每个叶子节点（NIL）是黑色的。
  4. 如果一个节点是红色的，则它的子节点必须是黑色的（不能有两个连续的红色节点）。
  5. 从任一节点到其每个叶子节点的所有路径都包含相同数量的黑色节点。

二、红黑树的旋转操作

红黑树通过旋转操作来维护树的平衡。旋转分为左旋和右旋两种操作。

  1. 左旋：将某个节点作为旋转中心，将其右子节点向上移动，代替该节点的位置，然后将该节点作为左子节点。
  2. 右旋：将某个节点作为旋转中心，将其左子节点向上移动，代替该节点的位置，然后将该节点作为右子节点。

三、红黑树的插入操作

红黑树的插入操作包括以下几个步骤：

  1. 执行二叉查找树的插入操作，将新节点涂成红色。
  2. 调整红黑树，使其满足红黑树的性质。
    插入操作可能导致以下几种情况：
  3. 叔叔节点是红色：此时，只需重新着色即可。
  4. 叔叔节点是黑色或不存在：
    （1）当前节点是父节点的左子节点，且父节点是祖父节点的左子节点，或者当前节点是父节点的右子节点，且父节点是祖父节点的右子节点。此时，只需进行一次旋转操作。
    （2）当前节点是父节点的左子节点，且父节点是祖父节点的右子节点，或者当前节点是父节点的右子节点，且父节点是祖父节点的左子节点。此时，需要进行两次旋转操作。

四、红黑树的删除操作

红黑树的删除操作包括以下几个步骤：

  1. 执行二叉查找树的删除操作。
  2. 调整红黑树，使其满足红黑树的性质。
    删除操作可能导致以下几种情况：
  3. 被删除节点是红色：直接删除，不影响红黑树的性质。
  4. 被删除节点是黑色：
    （1）被删除节点的子节点是红色：直接删除，并将子节点涂成黑色。
    （2）被删除节点的子节点是黑色：需要进行调整，以保持红黑树的性质。

五、红黑树的应用

 红黑树在计算机科学中有着广泛的应用，例如在Java的TreeMap和TreeSet中，以及C++的STL中。红黑树能够提供高效的查找、插入和删除操作，因此在需要维护有序数据集合的场景中，红黑树是一个很好的选择。

六、C语言模拟红黑树

以下是一个简单的C语言实现红黑树的示例：

#include <stdio.h>
#include <stdlib.h>

typedef enum {RED, BLACK} Color;

typedef struct Node {
    int data;
    Color color;
    struct Node *parent;
    struct Node *left;
    struct Node *right;
} Node;

/**
 * 创建并初始化一个节点。
 * @param data 节点中要存储的数据。
 * @return 返回指向新创建节点的指针。
 */
Node *createNode(int data) {
    // 分配内存给新节点
    Node *newNode = (Node *)malloc(sizeof(Node));
    if (newNode == NULL) {
        printf("Memory allocation failed!\n"); // 内存分配失败处理
        exit(1);
    }
    newNode->data = data; // 设置节点数据
    newNode->color = RED; // 新插入的节点默认为红色
    newNode->parent = NULL; // 初始化父节点为NULL
    newNode->left = NULL; // 初始化左子节点为NULL
    newNode->right = NULL; // 初始化右子节点为NULL
    return newNode; // 返回新创建的节点
}

/**
 * 左旋操作，用于平衡二叉搜索树（BST）。
 * 
 * @param root 指向当前树根节点的指针的地址。
 * @param x 需要进行左旋操作的节点。
 * 说明：函数不返回任何值，但会修改树的结构。
 */
void leftRotate(Node **root, Node *x) {
    Node *y = x->right;
    x->right = y->left;
    if (y->left != NULL)
        y->left->parent = x;
    y->parent = x->parent;
    if (x->parent == NULL)
        *root = y; // 如果x是根节点，更新根节点。
    else if (x == x->parent->left)
        x->parent->left = y; // 如果x是其父节点的左子节点，更新左子节点。
    else
        x->parent->right = y; // 如果x是其父节点的右子节点，更新右子节点。
    y->left = x;
    x->parent = y;
}

/**
 * 右旋操作
 * 
 * @param root 指向当前树根节点的指针的地址。
 * @param x 需要进行右旋操作的节点。
 * 说明：函数不返回任何值，但会修改树的结构。
 */
void rightRotate(Node **root, Node *y) {
    Node *x = y->left;
    y->left = x->right;
    if (x->right != NULL)
        x->right->parent = y;
    x->parent = y->parent;
    if (y->parent == NULL)
        *root = x;
    else if (y == y->parent->left)
        y->parent->left = x;
    else
        y->parent->right = x;
    x->right = y;
    y->parent = x;
}

/**
 * 插入修复函数
 * 该函数用于在红黑树中插入节点后，维护红黑树的性质。主要通过旋转和颜色的变换来保持红黑树的性质。
 * 
 * @param root 指向红黑树根节点的指针的地址
 * @param z 待插入的节点
 */
void insertFixup(Node **root, Node *z) {
    while (z != *root && z->parent->color == RED) {
        if (z->parent == z->parent->parent->left) {
            Node *y = z->parent->parent->right;
            if (y != NULL && y->color == RED) {
                z->parent->color = BLACK;
                y->color = BLACK;
                z->parent->parent->color = RED;
                z = z->parent->parent;
            } else {
                if (z == z->parent->right) {
                    z = z->parent;
                    leftRotate(root, z);
                }
                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                rightRotate(root, z->parent->parent);
            }
        } else {
            Node *y = z->parent->parent->left;
            if (y != NULL && y->color == RED) {
                z->parent->color = BLACK;
                y->color = BLACK;
                z->parent->parent->color = RED;
                z = z->parent->parent;
            } else {
                if (z == z->parent->left) {
                    z = z->parent;
                    rightRotate(root, z);
                }
                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                leftRotate(root, z->parent->parent);
            }
        }
    }
    (*root)->color = BLACK;
}

/**
 * 向红黑树中插入一个新节点
 * 
 * @param root 指向红黑树根节点的指针的地址
 * @param data 需要插入的数据
 */
void insert(Node **root, int data) {
    Node *z = createNode(data);
    Node *y = NULL;
    Node *x = *root;
    while (x != NULL) {
        y = x;
        if (z->data < x->data)
            x = x->left;
        else
            x = x->right;
    }
    z->parent = y;
    if (y == NULL)
        *root = z;
    else if (z->data < y->data)
        y->left = z;
    else
        y->right = z;
    insertFixup(root, z);
}


void inorderTraversal(Node *root) {
    if (root != NULL) {
        inorderTraversal(root->left);
        printf("%d ", root->data);
        inorderTraversal(root->right);
    }
}

int main() {
    Node *root = NULL;
    insert(&root, 10);
    insert(&root, 20);
    insert(&root, 30);
    insert(&root, 15);
    insert(&root, 18);

    inorderTraversal(root);
    printf("\n");

    return 0;
}

完整代码（包括红黑树节点输出以及删除节点操作）【链接】

结果
在这里插入图片描述

七、总结

 红黑树是一种自平衡二叉查找树，它能够保持树的平衡，从而保证查找、插入和删除的最坏情况时间复杂度为O( l o g n log_n logn​)。红黑树通过旋转操作和颜色变更来维护树的性质，适用于需要维护有序数据集合的场景。在Java和C++的STL中，红黑树得到了广泛的应用。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1623817.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

41-数组 _ 数组作为函数参数

41-数组 _ 数组作为函数参数

41-1 冒泡排序函数的设计 数组传参的时候&#xff0c;形参有2种写法&#xff1a; 1、数组 2、指针 往往我们在写代码的时候&#xff0c;会将数组作为参数传个函数 如&#xff1a;实现一个冒泡排序&#xff0c;将数组的数据排成升序 冒泡排序的核心思想&#xff1a; 1、两…
阅读更多...
新能源汽车小米su7

新能源汽车小米su7

小米su7汽车 function init() {const container document.querySelector( #container );camera new THREE.PerspectiveCamera( 20, window.innerWidth / window.innerHeight, 1, 50000 );camera.position.set( 0, 700, 7000 );scene new THREE.Scene();scene.background ne…
阅读更多...
kubebuilder（4）部署测试

kubebuilder（4）部署测试

将crd部署到k8s make install 日志&#xff1a; kustomize build config/crd | kubectl apply -f - customresourcedefinition.apiextensions.k8s.io/demoes.tutorial.demo.com created 查看下[rootpaas-m-k8s-master-1 demo-operator]# kubectl api-resources | grep demo de…
阅读更多...
yolov8 区域声光报警+计数

yolov8 区域声光报警+计数

yolov8 区域报警计数 1. 基础2. 报警功能2. 1声音报警代码2. 2画面显示报警代码 3. 完整代码4. 源码 1. 基础 本项目是在 yolov8 区域多类别计数 的基础上实现的&#xff0c;具体区域计数原理可见上边文章 2. 报警功能 设置一个区域region_points&#xff0c;当行人这一类别…
阅读更多...
【AIGC调研系列】Phi-3 VS Llama3

【AIGC调研系列】Phi-3 VS Llama3

2024-04-24日发布的Phi-3系列模型在多个方面展现出了对Llama-3的性能优势。首先&#xff0c;Phi-3-small&#xff08;7B参数&#xff09;在MMLU上的得分高于Llama-3-8B-Instruct模型&#xff0c;分别为75.3%和66%[1]。此外&#xff0c;具有3.8B参数的Phi-3 Mini在性能上优于Lla…
阅读更多...
解密Java多线程同步：掌握线程间同步与互斥技巧

解密Java多线程同步：掌握线程间同步与互斥技巧

哈喽&#xff0c;各位小伙伴们&#xff0c;你们好呀&#xff0c;我是喵手。 今天我要给大家分享一些自己日常学习到的一些知识点&#xff0c;并以文字的形式跟大家一起交流&#xff0c;互相学习&#xff0c;一个人虽可以走的更快&#xff0c;但一群人可以走的更远。 我是一名后…
阅读更多...
JavaScript:js实现在线五子棋人机(人人)对弈

JavaScript:js实现在线五子棋人机(人人)对弈

在线五子棋人机对弈 全部使用前端技术,使用HTML,CSS以及JS进行实现. 棋盘在后端就是一个15*15的二维数组 页面设计 页面设计的比较粗糙 主要使用js自带的canvas画布进行绘画 HTML代码如下: <div class"outer"><canvas id"canvas" height&qu…
阅读更多...
linux权限维持（四）

linux权限维持（四）

6.inetd服务后门 inetd 是一个监听外部网络请求 ( 就是一个 socket) 的系统守护进程&#xff0c;默认情况下为 13 端口。当 inetd 接收到 一个外部请求后&#xff0c;它会根据这个请求到自己的配置文件中去找到实际处理它的程序&#xff0c;然后再把接收到的 这个socket 交给那…
阅读更多...
B2B企业如何做好谷歌Google广告推广营销布局？

B2B企业如何做好谷歌Google广告推广营销布局？

当今全球化的商业环境中&#xff0c;B2B企业要想在激烈的市场竞争中脱颖而出&#xff0c;拓展海外市场成为了必经之路。而谷歌Google广告&#xff0c;作为全球最大的在线广告平台&#xff0c;无疑是企业触达全球潜在客户的黄金钥匙。云衔科技通过专业服务助力企业轻松开户与高效…
阅读更多...
CST初级教程 二

CST初级教程 二

本教程将讲解CST Studio的视窗操控的基本操作. 3D视窗的快捷操作 动态放大与缩小&#xff08;Dynamic Zoom&#xff09; 将鼠标指针移动到CST Studio图形视窗中&#xff0c;向上滚动鼠标滚轮&#xff0c;可动太放大图形视窗中的显示内容&#xff0c;向下滚动鼠标滚轮即可动态缩…
阅读更多...
非对称渐开线齿轮学习笔记分享

非对称渐开线齿轮学习笔记分享

最近有小伙伴遇到了非对称渐开线齿轮的加工问题，花了些时间学习了解一下，下面是总结的学习笔记，有兴趣的朋友可以瞅瞅： 目录： 为什么要采用非对称？ 非对称有什么优点？ 非对称齿形如何加工？ 非对称齿轮怎么测量？ 非对称齿轮建模 为什么要采用非对称？ 现在的传动要求…
阅读更多...
Linux：进程创建 进程终止

Linux：进程创建 进程终止

Linux&#xff1a;进程创建 & 进程终止 进程创建fork写时拷贝 进程终止退出码strerrorerrno 异常信号exit 进程创建 fork fork函数可以用于在程序内部创建子进程&#xff0c;其包含在头文件<unistd.h>中&#xff0c;直接调用fork()就可以创建子进程了。 示例代码&…
阅读更多...
【C语言】深入理解KMP算法及C语言实现

【C语言】深入理解KMP算法及C语言实现

一、KMP算法简介 KMP算法&#xff08;Knuth-Morris-Pratt算法&#xff09;是一种高效的字符串匹配算法&#xff0c;由Donald Knuth、James H. Morris和 Vaughan Pratt共同发明。KMP算法的核心思想是当一次字符比较失败时&#xff0c;利用已经得到的部分匹配信息&#xff0c;将模…
阅读更多...
JVM虚拟机监控及性能调优实战

JVM虚拟机监控及性能调优实战

目录 jvisualvm介绍 1. jvisualvm是JDK自带的可以远程监控内存&#xff0c;跟踪垃圾回收&#xff0c;执行时内存&#xff0c;CPU/线程分析&#xff0c;生成堆快照等的工具。 2. jvisualvm是从JDK1.6开始被继承到JDK中的。jvisualvm使用 jvisualvm监控远程服务器 开启远程监控…
阅读更多...
【Java框架】SpringMVC（三）——异常处理，拦截器，文件上传，SSM整合

【Java框架】SpringMVC（三）——异常处理，拦截器，文件上传，SSM整合

目录 异常处理解释局部异常处理全局异常 拦截器拦截器介绍作用:拦截器和过滤器之间的区别拦截器执行流程代码实现补充 文件上传依赖配置MultipartResolver编写文件上传表单页APIMultipartFileFile.separator必须对上传文件进行重命名代码示例 SpringMVC文件上传流程多文件上传 …
阅读更多...
mybatis中＜if＞条件判断带数字的字符串失效问题

mybatis中＜if＞条件判断带数字的字符串失效问题

文章目录 一、项目背景二、真实错误原因说明三、解决方案3.1针对纯数字的字符串值场景3.2针对单个字符的字符串值场景 四、参考文献 一、项目背景 MySQL数据库使用Mybatis查询拼接select语句中进行<if>条件拼接的时候&#xff0c;发现带数字的或者带单个字母的字符串失效…
阅读更多...
Coursera: An Introduction to American Law 学习笔记 Week 03: Property Law

Coursera: An Introduction to American Law 学习笔记 Week 03: Property Law

An Introduction to American Law 本文是 https://www.coursera.org/programs/career-training-for-nevadans-k7yhc/learn/american-law 这门课的学习笔记。 文章目录 An Introduction to American LawInstructors Week 03: Property LawKey Property Law TermsSupplemental Re…
阅读更多...
LM324的输出VOL与IOL你注意过吗？

LM324的输出VOL与IOL你注意过吗？

电路图 途中LMC6084 更改为LM324 故障现象 这个电路的输入输出表达式为 R30 两端电压等于0V 当J16 的4脚与2脚相等&#xff0c;等于5V&#xff08;或者4脚略大于2脚时&#xff09;7脚输出 约 500mV&#xff1b; 实际应该为0V左右才对.见下图 故障原因 上图运放输出低电平…
阅读更多...
AI重塑数字安全，安恒信息行胜于言

AI重塑数字安全，安恒信息行胜于言

有人曾言&#xff1a;所有行业都值得基于人工智能技术重做一遍。 深以为然。如今&#xff0c;数字安全产业面临着一次重要的重塑机遇。以大模型为代表的人工智能技术正深刻影响着数字安全市场格局、产品研发、技术方案以及运营服务。产业界已形成共识&#xff0c;即谁能抓住人…
阅读更多...
Nginx+Lua+OpenResty（详解及使用）

Nginx+Lua+OpenResty（详解及使用）

一、 Nginx简介 Nginx是一个高性能的Web服务器和反向代理的软件。 Web服务器&#xff1a;就是运行我们web服务的容器&#xff0c;提供web功能&#xff0c;还有tomcat也提供类似的功能。 代理是软件架构和网络设计中&#xff0c;非常重要的一个概念。 二、Nginx的反向代理&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023