目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
4.1 M/M/1 单服务台单通道排队模型
4.2 M/M/k 多服务台排队模型
4.3 M/G/1 和 G/M/1 模型
5.完整程序
1.程序功能描述
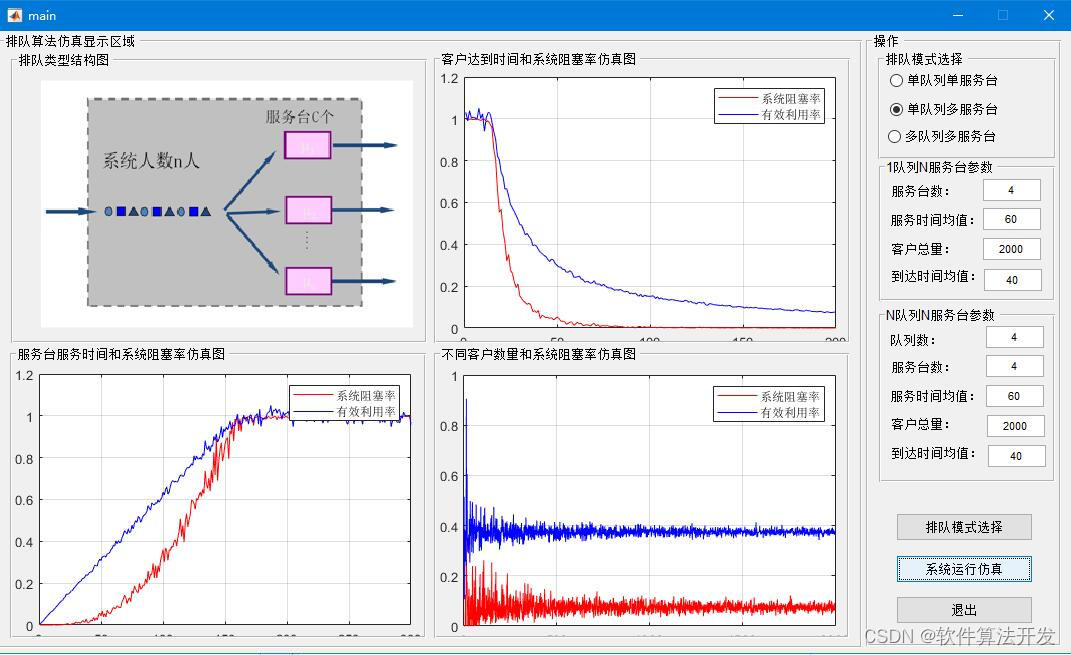
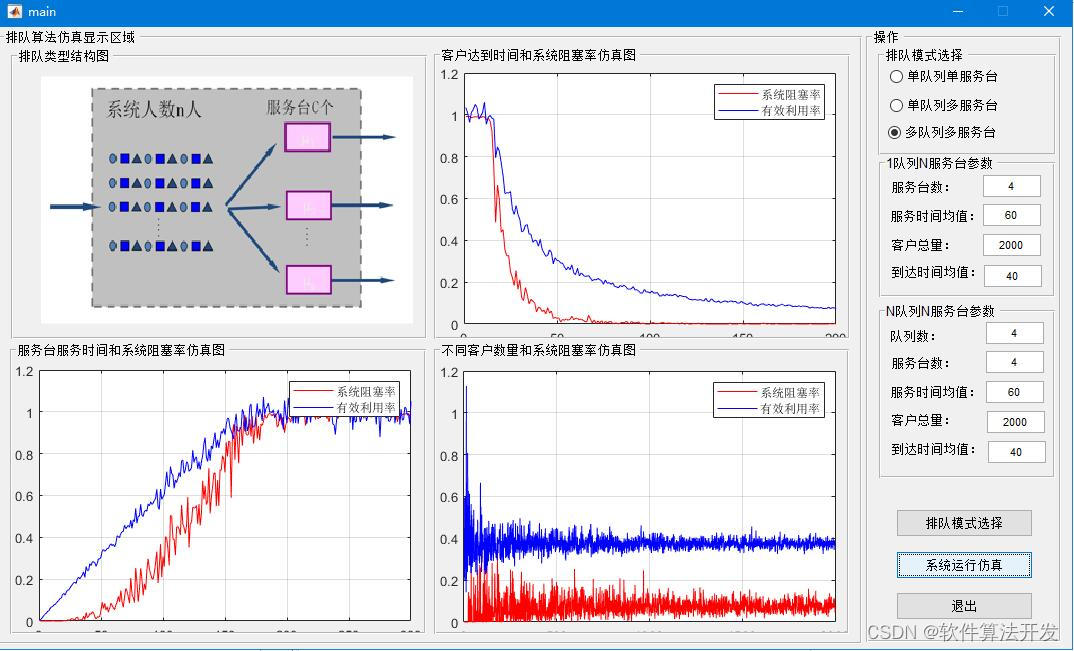
排队算法的matlab仿真,带GUI界面。分别仿真单队列单服务台,单队列多服务台以及多队列多服务台三种排队方式。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行

3.核心程序
function[Blocking_Rate,Use_Rate]=func_mms2(Time_Arrival,Time_Server,Num_queue,Num_People,Num_Server);
%三行依次为:到达时间间隔,服务时间,等待时间
People_State = zeros(3,round(Num_People/Num_queue)+1);
%到达时间服从指数分布
People_State(1,:) = exprnd(Time_Arrival,1,round(Num_People/Num_queue)+1);
%服务时间服从指数分布
People_State(2,:) = exprnd(Time_Server,1,round(Num_People/Num_queue)+1);
%初始化
for i=1:Num_Server
People_State(3,1:Num_Server)=0;
end
%累积到达时间
Time_Arrival_sum = cumsum(People_State(1,:));
People_State(1,:) = Time_Arrival_sum;
%离开时间
Leave_Time(1:Num_Server)= sum(People_State(:,1:Num_Server));
Server_desk = Leave_Time(1:Num_Server);
for i=(Num_Server+1):round(Num_People/Num_queue)+1
%当时服务台最早离开的顾客的离开时间减去第i个顾客的到达时间
if Time_Arrival_sum(i)>min(Server_desk)
People_State(3,i)=0;
else
People_State(3,i)=min(Server_desk)-Time_Arrival_sum(i);
end
Leave_Time(i)=sum(People_State(:,i));
for j=1:Num_Server
if Server_desk(j)==min(Server_desk)
Server_desk(j)=Leave_Time(i);
break
end
end
end
Max_time = Leave_Time(round(Num_People/Num_queue)+1)*2;
Server_desk(1:Num_Server) = Max_time;
Blocking_Num = 0;
Blocking_Line = 0;
16_022m
4.本算法原理
排队系统是基本的离散事件系统,了解掌握离散事件系统是研究排队系统仿真不可或缺的前提。离散事件系统是指其状态变量只在某些离散时间点上发生变化的系统。这种系统的状态通常只取有限个离散值,对应于系统部件的好坏、忙闲及待处理工件个数等可能的物理状况。而这些状态的变化则由于诸如某些环境条件的出现或消失、系统操作的启动或完成等各种事件的发生而引起。离散事件系统大量地存在于我们的周围,常见的有排队系统、库存管理系统等。利用仿真技术对这些系统进行研究分析,可以了解它们的动态运行规律,从而帮助人们做出最佳的选择或决定。排队论(Queueing Theory)是一门研究系统中顾客和服务台交互行为的学科,主要关注在有限资源约束下,顾客到达系统并等待服务的过程。它广泛应用于通信网络、生产调度、服务行业等多种领域,用于优化系统性能,减少等待时间,提高资源利用率。
4.1 M/M/1 单服务台单通道排队模型
基本设定:
- 客户(顾客)按照泊松过程到达,即平均每单位时间到达的客户数λ遵循泊松分布。
- 每个客户的服务时间独立同分布,服从指数分布,平均服务时间为1/μ。
- 系统中只有一个服务台,服务台空闲时立即服务下一个客户。
4.2 M/M/k 多服务台排队模型
基本设定:
- 同样假定客户到达和服务时间符合M/M/1模型的设定,但系统中有k个相同的服务台。
4.3 M/G/1 和 G/M/1 模型
延伸模型:
- M/G/1模型:客户到达仍然服从泊松过程,但服务时间不再是指数分布,而是任意分布G。
- G/M/1模型:服务时间服从指数分布,而客户到达不再遵循泊松过程,到达间隔时间服从任意分布G。
这些模型的分析通常需要更复杂的数学手段,例如嵌套积分、矩阵分析和变换技术,难以用简洁的公式表示其性能指标,一般需要借助高级数学工具求解。
排队系统可以扩展到更为复杂的场景,比如有限容量缓冲区、优先级排队、非工作时段、可中断服务等。这些复杂模型往往需要运用Markov链理论、生灭过程、嵌入马尔科夫链等方法进行深入分析。在实际应用中,排队论的目标通常是确定各种性能指标(如等待时间、利用率、服务水平等),以便设计出合理的服务策略和资源分配方案,以最小化成本或最大化服务质量。通过对排队模型的研究,我们可以建立系统的数学模型,并利用数值计算或解析方法求解相关指标,进而指导实际运营决策。
5.完整程序
VVV