1.Attention
Attention是Transformer的核心部分,Attention机制帮助模型进行信息筛选,通过Q,K,V,对信息进行加工
1.1 attention计算公式
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V Attention(Q,K,V)=softmax(dkQKT)V
1.2 attention计算流程
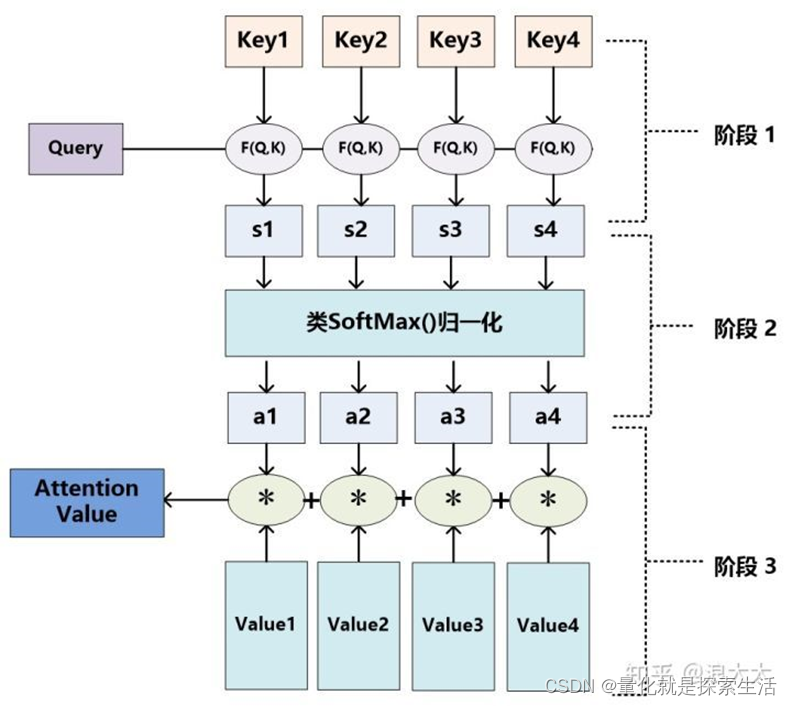
1.3 Softmax attention
Self-attention的Q,K,V同源,都是输入序列X的线性变化,在实际生产过程中K与V相同。
F为token维度,DM为投影维度
Q
=
x
W
Q
,
W
Q
∈
R
F
×
D
K
=
x
W
K
,
W
K
∈
R
F
×
D
V
=
x
W
V
,
W
V
∈
R
F
×
M
\begin{aligned} & Q=x W_Q, W_Q \in \mathbb{R}^{F \times D} \\ & K=x W_K, W_K \in \mathbb{R}^{F \times D} \\ & V=x W_V, W_V \in \mathbb{R}^{F \times M} \end{aligned}
Q=xWQ,WQ∈RF×DK=xWK,WK∈RF×DV=xWV,WV∈RF×M
其中
Q
∈
R
N
×
D
K
∈
R
N
×
D
V
∈
R
N
×
M
\begin{aligned} & Q \in \mathbb{R}^{N \times D} \\ & K \in \mathbb{R}^{N \times D} \\ & V \in \mathbb{R}^{N \times M} \end{aligned}
Q∈RN×DK∈RN×DV∈RN×M
S
A
(
x
)
=
softmax
(
Q
K
T
D
)
V
S A(x)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{D}}\right) V
SA(x)=softmax(DQKT)V
向量a是词嵌入向量,三个W矩阵是对a的线性变化
1.3.1 图解 Softmax Attention
仅考虑Decoder
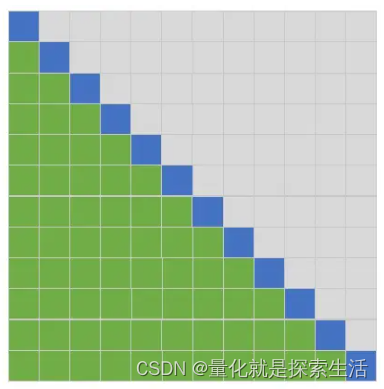
行和列都表示位置;蓝色表示当前token,绿色表示参与当前token计算的其它token的位置。
Transformer中Decoder采用的方式:只能看当前token左边的token。
1.3.2 复杂度计算
对于矩 A ∈ R ( N , M ) A \in \mathbb{R}^{(N, M)} A∈R(N,M)和 B ∈ R ( M , L ) B \in \mathbb{R}^{(M, L)} B∈R(M,L),它们的矩阵乘法共需要 N × L × M N \times L \times M N×L×M次乘法运算。总复杂度 O ( N L M ) O(N L M) O(NLM)。
回到Transformer的复杂度问题上,前面提到Softmax Attention的计算主要包含两次矩阵乘法操作。
第一次矩阵乘法是
Q
×
K
T
Q \times K^T
Q×KT,结合上文关于矩阵乘法复杂度的结论和这两个矩阵的大小,可知
Q
×
K
T
Q \times K^T
Q×KT的复杂度为
O
(
N
2
D
)
O\left(N^2 D\right)
O(N2D)。
第二次矩阵乘法是softmax的结果与 V V V 的乘积。 softmax输出的矩阵大小为 N × N N \times N N×N ,矩阵 V V V的大小为 N × D N \times D N×D,所以这一次矩阵乘法的复杂度为 O ( N 2 D ) O\left(N^2 D\right) O(N2D)。
因为这两次矩阵乘法是顺序执行的,所以总的复杂度为它们各自复杂度之和。因为这两个复杂度相等,相加只是引入了一个常数项,所以可以忽略,因此Softmax Attention总的复杂度就为 O ( N 2 D ) O\left(N^2 D\right) O(N2D)
当我们只关心复杂度与序列长度 N N N之间的关系时,可以忽略 D D D并将其写为 O ( N 2 ) O\left(N^2 \right) O(N2)。
这就是通常说的Transformer计算复杂度随序列长度呈二次方增长的由来。容易看到,Transformer的空间复杂随序列长度也呈二次方增长,即空间复杂度也为
O
(
N
2
)
O\left(N^2 \right)
O(N2)
。
1.4 attention的问题与优化
传统attention存在上下文长度的约束问题,且速度慢,内存占用大
优化方向:1. 上下文 2. 内存
Attention和FFN的复杂度:长序列难题,对于base版来说,当序列长度不超过1536时,Transformer的复杂度都是近乎线性的;当序列长度超过1536时,Transformer的计算量逐渐以Attention为主,复杂度慢慢趋于二次方,直到长度超过4608,才真正以二次项为主。
2. Attention 变种
2.1 稀疏 attention(Sparse Attention)
核心在于减少每个token需要attend的token数量。
2.1.1 Factorized Self-Attention (Sparse Transformer)
Paper:Generating Long Sequences with Sparse Transformers (2019)
提出了两种稀疏Attention方法:Strided Attention和Fixed Attention。这二者均可将Transformer的
O
(
N
2
)
O(N^2)
O(N2)复杂度降低至
O
(
N
N
)
O(N\sqrt{N})
O(NN) 。
Factorized Self-Attention的一个基础假设是:在Softmax Attention中,真正为目标token提供信息的attended token非常少。
图片和自然语言领域,临近词语,像素又理论上的更高相关性,此时的Attention Weights很像CNN,卷积神经网络仅考虑临近像素之间的
Strided Attention (跨步注意力)
SA1:每个token只能Attend它左边相邻的L个token。

SA2:每个token只能Attend它左边部分token,这些attened token用如下方法选出:从自己开始往左边数,每隔L就会有一个token可以attend

使用方式:
- 每个Transformer Block 交替使用
- SA1 与 SA2在一次Attend中 联合使用
- 基于trm的多头机制,对不同的SA 多头使用
Fixed Attention 固定注意力
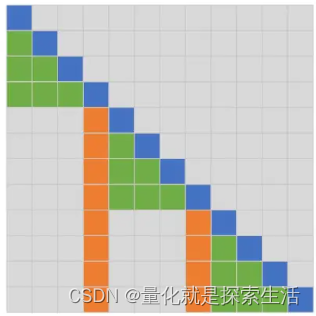
先看FA2,如图中橙色区域。橙色区域的位置是固定的,即从左往右数,每隔L个位置,选中一个token。
理解了FA2,FA1的选择方式就会容易理解了。对于每个当前token(蓝色),往它左边遍历(绿色),直到遇到第一个FA2选中的token(橙色)。
Fixed Attention的使用方法和上文介绍的Strided Attention的三种方法一致(交替使用、联合使用、多头使用)
Strided Attention适用于图像、音频;Fixed Attention适用于文本。
Strided Attention在attended token的位置上做了强假设:哪些位置的token应该被attened,与当前token位置强相关。作者们认为这种适合图像、音频这类数据。而在文本上这类假设不成立。所以在Fixed Attention中,哪些位置的token应该被attened,与当前token位置无关。图像、音频的局部信息很重要;而文本全局信息更重要。
2.1.2 Blockwise Self-Attention
Paper:Blockwise Self-Attention for Long Document Understanding (2019)
核心: 通过分块来降低Softmax Attention的计算复杂度,方法简单,且实验效果较好。
并非全量匹配,而是分块匹配
原则为shifting one position
例如:
Index
(
Q
)
=
[
2
,
3
,
1
]
\operatorname{Index}(Q)=[2,3,1]
Index(Q)=[2,3,1]
很简单,
Q
1
Q_1
Q1选择
K
2
K_2
K2和
V
2
V_2
V2,
Q
2
Q_2
Q2选择
K
3
K_3
K3和
V
3
V_3
V3,
Q
3
Q_3
Q3选择
K
1
K_1
K1和
V
1
V_1
V1。
2.1.3 Longformer
paper:Longformer: The Long-Document Transformer (2020)
Key Contribution:设计了多种不同的Local Attention和Global Attention方法。
分为三个部分:
Sliding Window based Attention(SW-Attention)
同 SW-1
Dilated Sliding Window based Attention(DSW-Attention)
同 SW-2
Global Attention(G-Attention)

绿色token是SW-Attention会attend到的token。橙色token是在G-Attention中额外选中的token。以第五行的当前token为例(橙色),因为它是被额外选中的token,所以它会attend它左边的所有token。图中用黄色标出了相对于SW-Attention之外的额外被attended的token。此外,其它所有token也需要attend到第五个token,参见图中最后四行中的靠左黄色列。
2.1.4 Local attention and Memory-compressed attention
Paper: Generating wikipedia by summarizing long sequences (2018)
Key Contribution: 提出了Local Attention和Memory-compressed attention。Local Attention的计算复杂度随序列长度增长呈线性增长;Memory-compressed attention可以将计算复杂度减少固定常数倍(超参控制)。
Local attention
控制分块大小,每个token仅仅attend固定分块
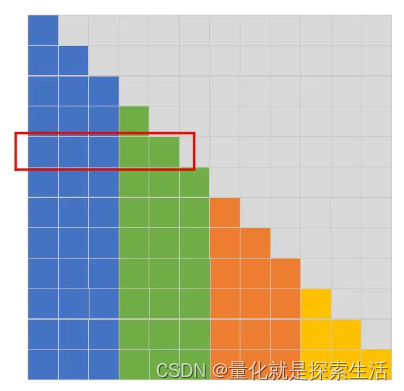
与前文 Blockwise Self-Attention 不同,前者为固定分块大小,后者为固定分块数量。
Memory-compressed Attention
核心思路:使用额外的卷积来降低K和V的序列长度
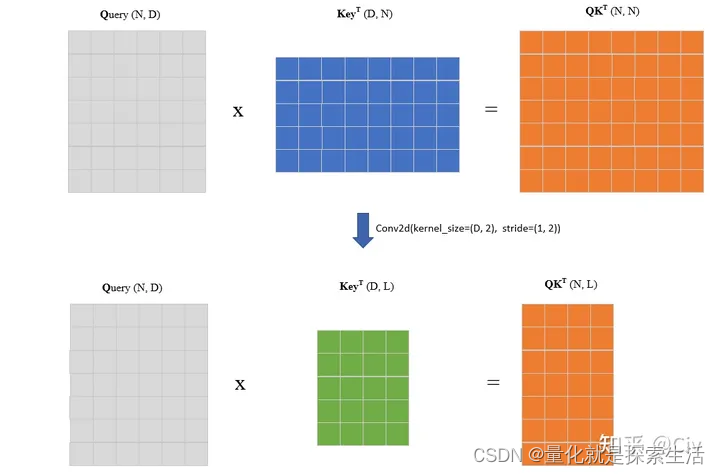
计算复杂度从
O
(
N
2
)
O(N^2)
O(N2)降低到
O
(
N
L
)
O(NL)
O(NL)
2.2 Reformer
paper: Reformer: the efficient Transformer(2020)
Key contribution: 1)提出了LSH-attention,能够将Transformer的复杂度由
O
(
N
2
)
O(N^2)
O(N2)降低至
O
(
N
l
o
g
N
)
O(NlogN)
O(NlogN);2)将Transformer中的跳跃连接改为了“可逆跳跃连接”,这样在网络的前向过程中不用为后续的梯度计算存储激活值,能够极大降低训练过程的存储开销。
核心:降低基于Transformer的模型在训练阶段的存储开销。
空间开销估算
0.5BTRM为例,64K序列长度,1K embedding, batch size 8
- TRM参数量 0.5B * 4 Byte = 2G
- self-attention激活值 64K * 1K * 8 * 4 Byte = 2G
- 两个FFN,一个是激活值的4倍,一个是一倍,总共10G
- 矩阵计算,64K*64K,16G
Locality-Sensitive Hashing Attention(LSH-attention)
核心思路,找到权重较大的token,不需要所有token参与计算
即在不做向量点积运算的前提下,粗略估算两向量的余弦相似度。
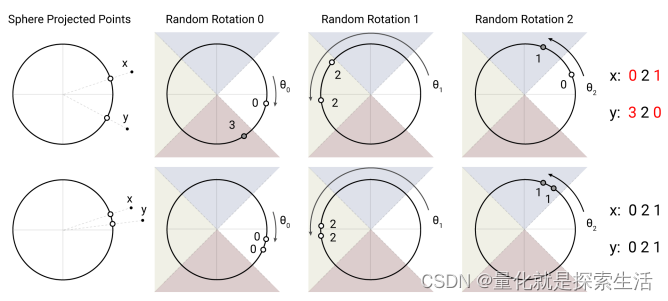
步骤:
- 将两个向量投影在单位超球面上(二范数为1)
- 对超球面施加若干次随机转动
- 记录下每次转动后的区块,(argmax实现,扩展成2*N的向量(x,y,-x,-y),最大值所在维度)
- 多次转动后,每个token可获得一个hash值
- 根据hash值对token重排序,然后分块attend
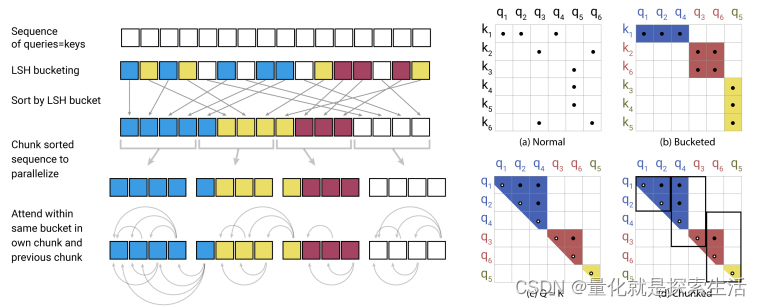
可以将复杂度降低至 O ( N l o g N ) O(NlogN) O(NlogN)
Reversible Transformer
使用可逆网络的思想,减少中间激活值存储,
在attention+FFN架构中,已知前一层
X
1
,
X
2
X_1, X_2
X1,X2,计算下一层
Y
1
,
Y
2
Y_1, Y_2
Y1,Y2
Y
1
=
X
1
+
Attention
(
X
2
)
Y
2
=
X
2
+
FeedForward
(
Y
1
)
\begin{aligned} & Y_1=X_1+\operatorname{Attention}\left(X_2\right) \\ & Y_2=X_2+\operatorname{FeedForward}\left(Y_1\right) \end{aligned}
Y1=X1+Attention(X2)Y2=X2+FeedForward(Y1)
则可以在已知
Y
1
,
Y
2
Y_1, Y_2
Y1,Y2的情况下,恢复一层
X
1
,
X
2
X_1, X_2
X1,X2
代价多计算一次attention和FFN
X
2
=
Y
2
−
FeedForward
(
Y
1
)
X
1
=
Y
1
−
Attention
(
X
2
)
\begin{aligned} & X_2=Y_2-\operatorname{FeedForward}\left(Y_1\right) \\ & X_1=Y_1-\operatorname{Attention}\left(X_2\right) \end{aligned}
X2=Y2−FeedForward(Y1)X1=Y1−Attention(X2)
唯一需要考虑的是激活函数是否可逆,Relu和Gelu不可逆,需要注意
2.3 Adaptive Attention
paper:Adaptive Attention Span in Transformers
Key contribution: 提出了一种对不同attention head自适应选择attention长度的方法。
对于权重计算公式的改进:
a
i
j
=
exp
(
q
i
⋅
k
j
)
∑
m
=
0
i
exp
(
q
i
⋅
k
m
)
a_{i j}=\frac{\exp \left(q_i \cdot k_j\right)}{\sum_{m=0}^i \exp \left(q_i \cdot k_m\right)}
aij=∑m=0iexp(qi⋅km)exp(qi⋅kj)
改进为:
a
i
j
=
d
(
i
−
j
)
⋅
exp
(
q
i
⋅
k
j
)
∑
m
=
0
i
d
(
i
−
m
)
⋅
exp
(
q
i
⋅
k
m
)
a_{i j}=\frac{d(i-j) \cdot \exp \left(q_i \cdot k_j\right)}{\sum_{m=0}^i d(i-m) \cdot \exp \left(q_i \cdot k_m\right)}
aij=∑m=0id(i−m)⋅exp(qi⋅km)d(i−j)⋅exp(qi⋅kj)
函数d定义:
d
(
x
)
=
min
[
max
[
1
R
(
R
+
z
−
x
)
,
0
]
,
1
]
d(x)=\min \left[\max \left[\frac{1}{R}(R+z-x), 0\right], 1\right]
d(x)=min[max[R1(R+z−x),0],1]
其中R为超参数,z是需要学习的参数
函数图像为:
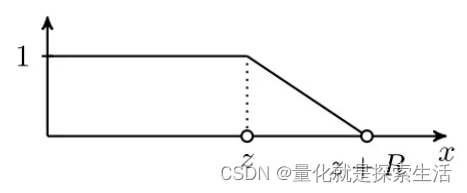
有效距离内,完美attaend,有效举例外衰减,类似lasso
参考
https://zhuanlan.zhihu.com/p/634406691