传染病模型及其变体

1. SI模型

在该模型里面，群体中只有两种人：易感者和感染者。
感染者每天会感染一定的数量的易感者。
S表示易感者（尚未感染但是容易被感染的人） 的数量
I表示感染者（已经感染的人）的数量
N表示人口总数
r表示一个感染者平均每天感染易感者的人数
那么每天易感者和感染者的数量变化为
$$\begin{array}{rl}dS& =\frac{-rSI}{N}\\ dI& =\frac{rSI}{N}\end{array}$$

1.1代码

import numpy as np   # 科学计算工具包
import matplotlib.pyplot as plt  # 画图工具包

plt.rcParams["font.family"] = 'Arial Unicode MS'  # 用来正常显示中文
# 定义SI函数——根据SI模型计算每天新增的易感人数和感染人数，返回累计人数
def SI(si,dt):
    S,I = si          # 每天初始SI的数值
    dS = -(r*I*S)/N   # 易感者微分方程
    dI = r*I*S/N      # 感染者微分方程
    S = 0 if S+dS*dt<=0 else S+dS*dt      # 当天易感者人数    
    I = N if I+dI*dt>=N else I+dI*dt      # 当天感染者人数
    return [S, I]

def calculate(func,si,days):  
    dt = 1
    t = np.arange(0,days,dt) # 设置时间步
    res = []
    for itm in t:
        si=func(si,dt)      # 运行SI模型函数
        res.append(si)      # 存储每天人数结果
    return np.array(res)

# 画图函数
def plot_graph(np_res): 
    plt.figure(figsize=(10,6),dpi=300)
    plt.plot(np_res[:,0])
    plt.plot(np_res[:,1])
    plt.title("SI模型")
    plt.xlabel("天数")
    plt.ylabel("人数")
    plt.legend(['易感者','感染者'])
    plt.show()
    

N = 10000
I = 1
r = 1
days = 50
si= [N-I,    # 易感人数
       I]    # 感染人数

result = calculate(SI,si,days)
plot_graph(result)

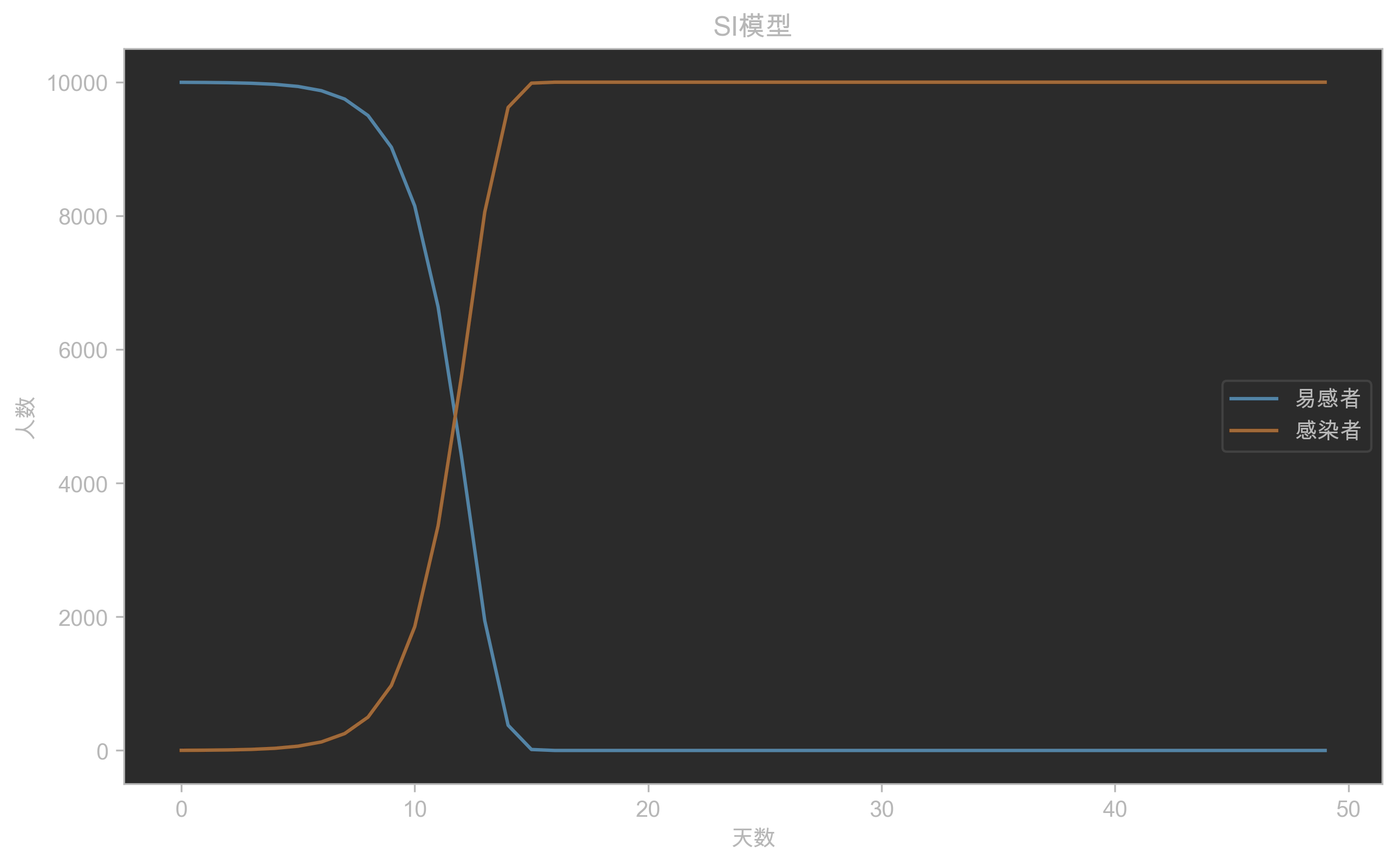
2. SIS模型

在该模型里面，群体中依然只有两种人：易感者和感染者。

感染者每天会感染一定的数量的易感者，同时每天会有一定数量的感染者康复，但是他们康复之后依然有可能被感染。

$S$表示易感者（尚未感染但是容易被感染的人） 的数量

$I$表示感染者（已经感染的人）的数量

$N$表示人口总数

$r$表示一个感染者平均每天感染易感者的人数

$\mu$ 表示感染者每天康复的比例

那么每天易感者和感染者的数量变化为

$$\begin{array}{rl}dS& =\frac{-rSI}{N}+\mu I\\ dI& =\frac{rSI}{N}-\mu I\end{array}$$

2.1 代码

# 定义SIS函数——根据SIS模型计算每天新增的易感人数和感染人数，返回累计人数
def SIS(sis,dt):
    S,I = sis          # 每天初始SI的数值
    dS = -(r*I*S)/N + u*I   # 易感者微分方程
    dI = r*I*S/N - u*I     # 感染者微分方程
    S = 0 if S+dS*dt<=0 else S+dS*dt    # 当天易感者人数
    I = N if I+dI*dt>=N else I+dI*dt    # 当天感染者人数
    return [S, I]

def calculate(func,sis,days):  
    dt = 1
    t = np.arange(0,days,dt) # 设置时间步
    res=[]
    for itm in t:
        sis=func(sis,dt)      # 运行SI模型函数
        res.append(sis)      # 存储每天人数结果
    return np.array(res)

# 画图函数
def plot_graph(np_res): 
    plt.figure(figsize=(10,6),dpi=300)
    plt.plot(np_res[:,0])
    plt.plot(np_res[:,1])
    plt.title("SIS模型")
    plt.xlabel("天数")
    plt.ylabel("人数")
    plt.legend(['易感者','感染者'])
    plt.text(10,4500,'N=%d \nI=%d \nr=%2.1f \nu=%2.1f' % (N,I,r,u), bbox={
   'facecolor': 'red', 'alpha': 0.4, 'pad': 8})
    final = [round(x) for x in result[-1]]  # 取整表示
    plt.text(90,final[0],final[0])
    plt.text(93,final[1],final[1])
    plt.show()

# 赋值绘图
N = 10000
I = 1
r = 0.6
u = 0.2
days = 100

sis= [N-I,    # 易感人数
       I]    # 感染人数

result = calculate(SIS,sis,days)
plot_graph(result)
print(result[-1])

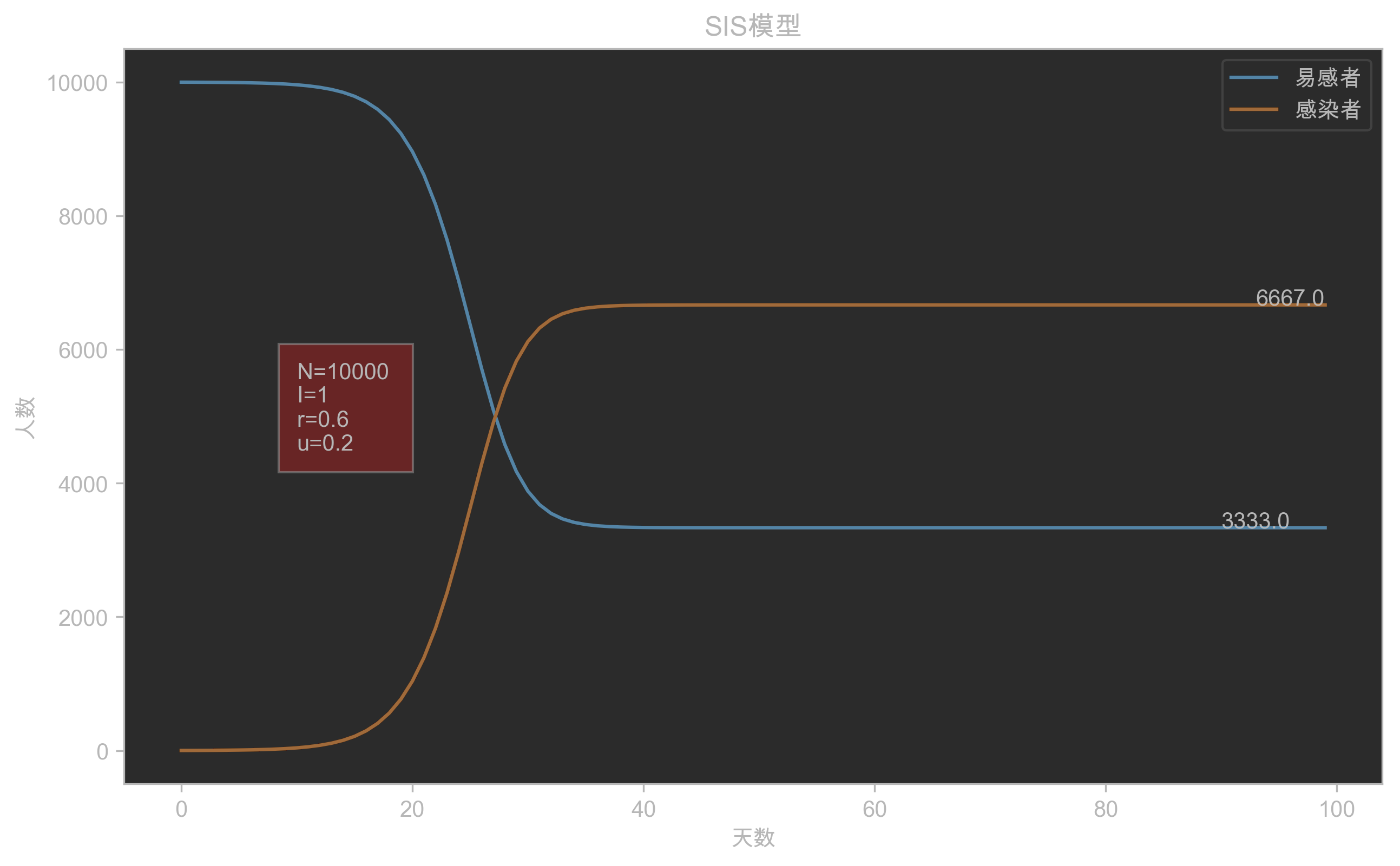
可以看出，在SIS模型中，并非所有的人都会被感染，最终感染人数为：

$$I=N(1-\frac{u}{r})$$

3. 基本再生数 basic reproductive number

这里，从SIS模型中引出了一个概念，就是基本再生数，其定义为：

R