一 线段树
1.概念
线段树可以理解为一个二叉树,如果是利用线段树求区间的和,那么每个结点的权值维护的是结点所维护区间的和,再将该区间一分为二,分别交由左右儿子维护。
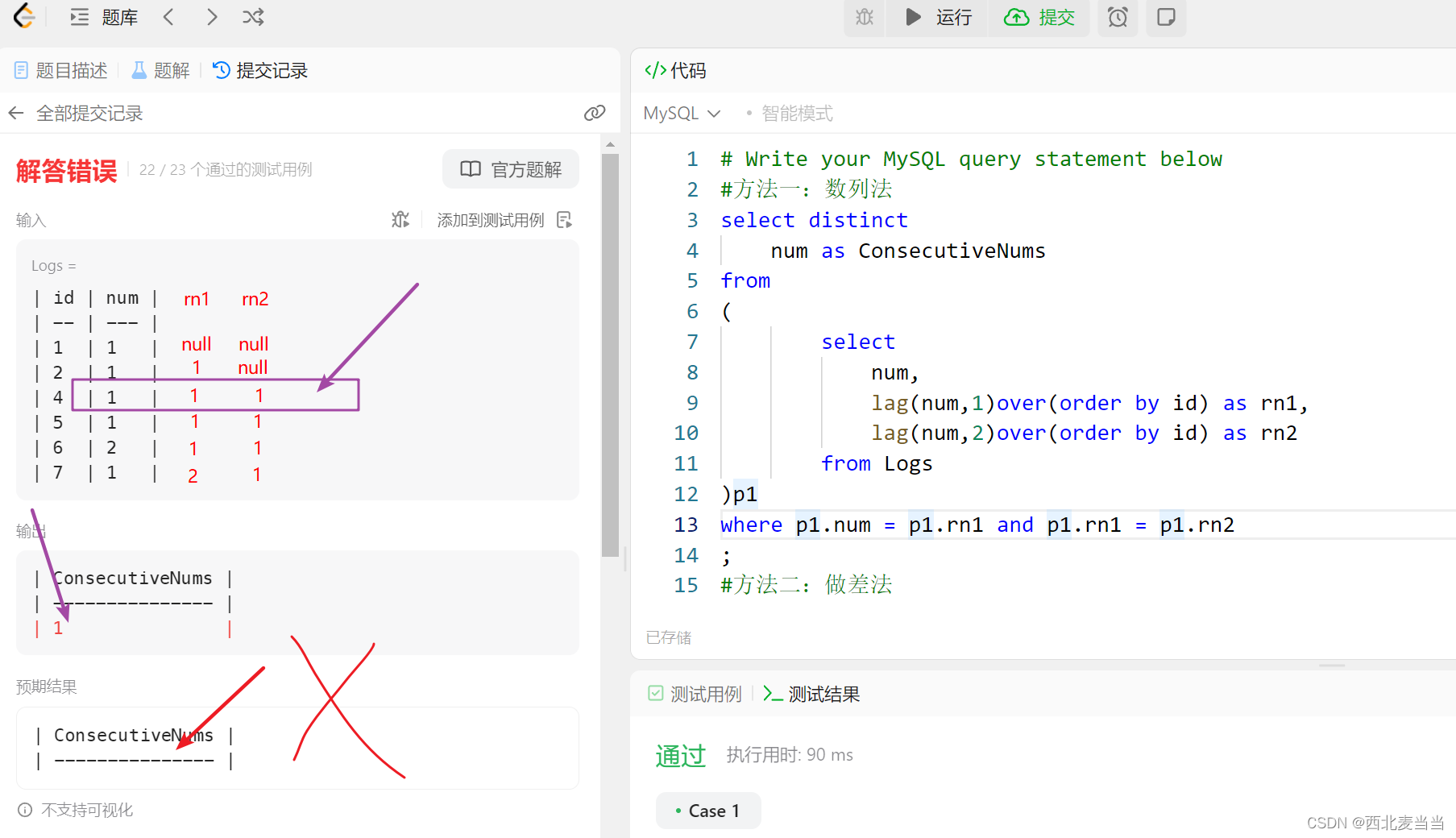
拿区间1 - 4的和来举例子,
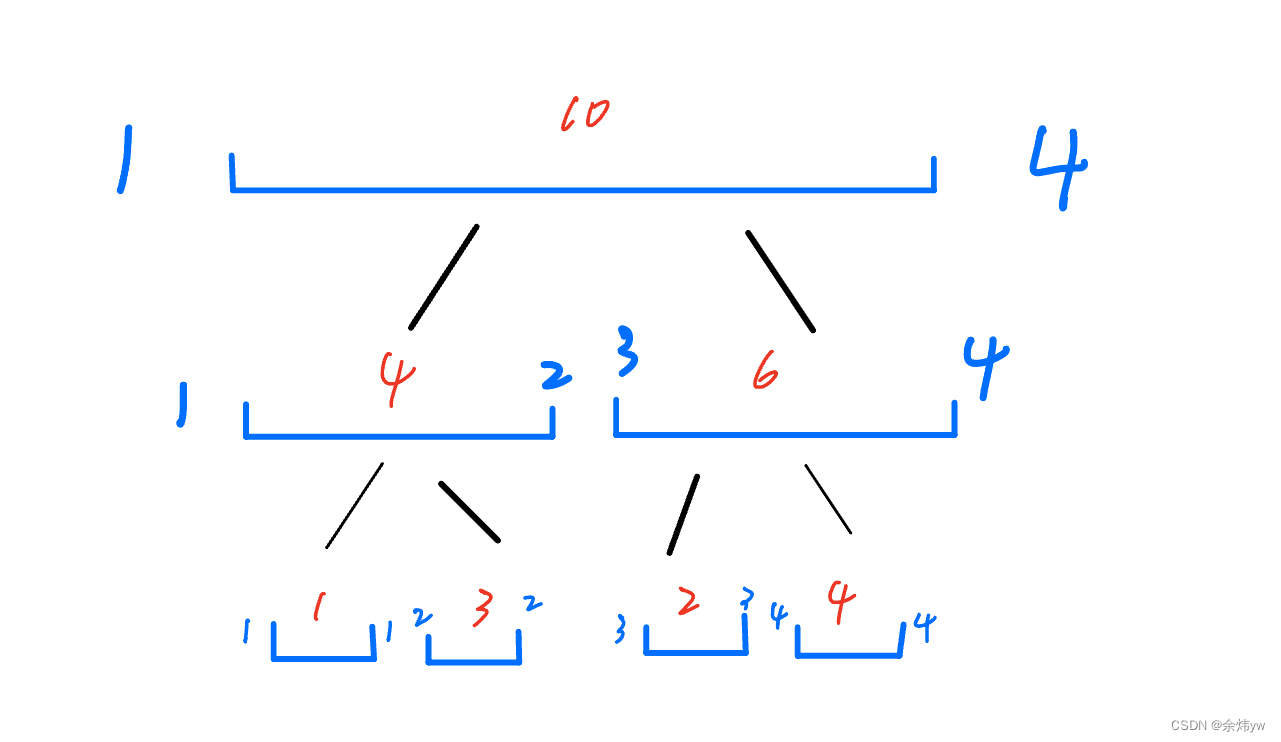
根结点维护的是区间1 到 4,结点权值是该区间的和,再将区间一份为二,其左儿子维护的是 1 - 2,右儿子维护的是 3 - 4 ,以此类推,直到结点维护的区间长度为1。
不难看出,每个节点的权值等于左右儿子的权值之和。
2.基本步骤
1.构造线段树
清楚了线段树的概念后,很容易构造线段树,一般算法题都是通过数组模拟二叉树,本文也采用这种方式。
struct Tree {
int l, r, weight;
} tree[N];
using namespace std;
void build_tree(int i, int l, int r) {
if (l == r) {
tree[i] = {l, r, w[l]};
return;
}
int mid = l + r >> 1;
//构建左子树
build_tree(i<<1, l, mid);
//构建右子树
build_tree(i<<1|1, mid + 1, r);
//节点权值
int sum = tree[i * 2].weight + tree[i * 2 + 1].weight;
//更新区间
tree[i] = {l,r,sum};
}2.区间查询
从根节点开始找目标区间
1.结点维护的区间是目标区间的子集,直接返回结点权值
2.左子树与目标区间有交集,递归左子树
2.右子树与目标区间有交集,递归右子树
4.返回sum
拿查找2-3区间和举例
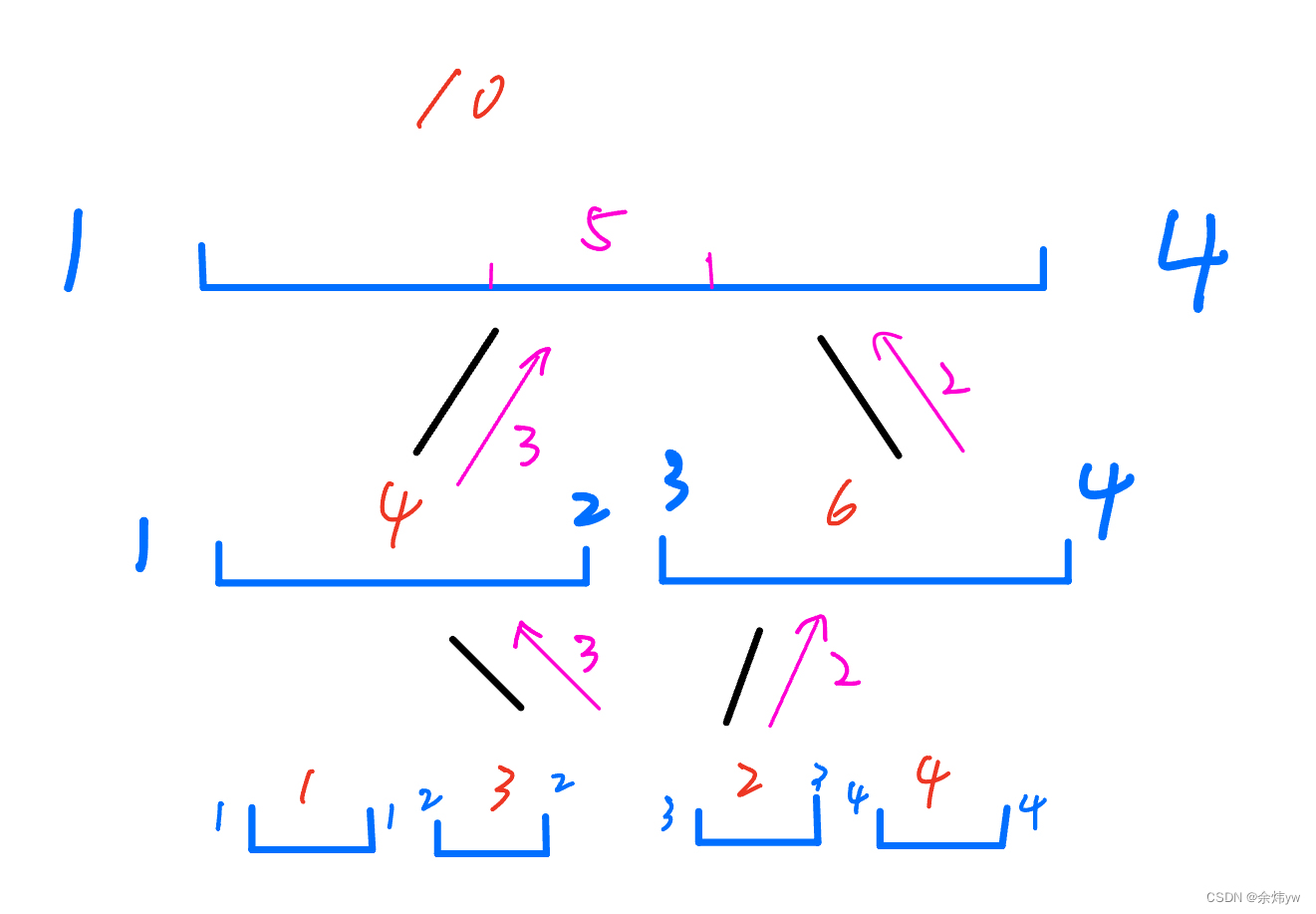
从根节点开始,目标区间和左子树有交集,递归左子树,目标区间和右子树有交集 ,递归右子树;
接着看根节点左儿子,目标区间只和右子树有交集,递归右子树,
看根节点右儿子,目标区间只和左子树有交集,递归左子树,
再向下递归发现,节点维护区间刚好是目标区间的子集,直接返回权值,结束向下递归。
代码
int query(int i,int l,int r){
//结点维护区间是目标区间的子集,直接返回权值
if(tree[i].l>=l&&tree[i].r<=r)return tree[i].weight;
int mid = tree[i].l + tree[i].r >>1;
int sum = 0;
if(l<=mid) sum += query(i*2,l,r);
if(r>mid)sum+= query(i*2+1,l,r);
return sum;
}3.区间修改
从根节点开始找目标区间
1.结点维护的区间是目标区间的子集,修改权值,返回
2.左子树与目标区间有交集,递归左子树
2.右子树与目标区间有交集,递归右子树
4.更新结点权值(pushup)
拿给2-3区间加1和举例
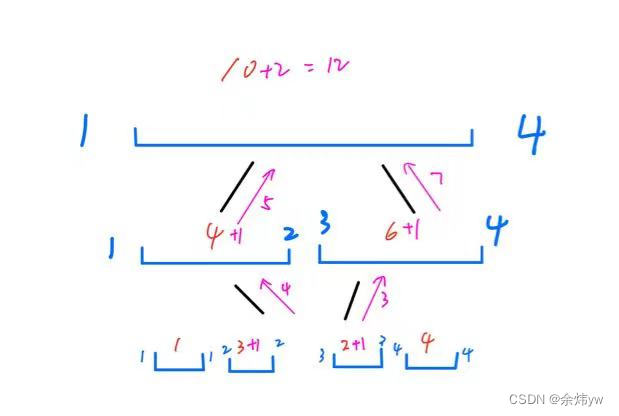
从根节点开始,目标区间和左子树有交集,递归左子树,目标区间和右子树有交集 ,递归右子树;
接着看根节点左儿子,目标区间只和右子树有交集,递归右子树,
看根节点右儿子,目标区间只和左子树有交集,递归左子树,
再向下递归发现,节点维护区间刚好是目标区间的子集,直接修改权值,结束向下递归。
代码
void pushup(int i){
tree[i].weight = tree[i<<1].weight + tree[i<<1|1].weight;
}
void modify(int i, int l, int r,int v)
{
if(tree[i].l>=l&&tree[i].r<=r) tree[i].weight+=v*(tree[i].r - tree[i].l+1);
else{
int mid = tree[i].l + tree[i].r >>1;
if(l<=mid) modify(i<<1,l,r,v);
if(r>mid) modify(i<<1|1,l,r,v);
pushup(i);
}
}
例题
1.动态求连续区间和
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列[a,b]的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含n个整数,表示完整数列。
接下来 m 行,每行包含三个整数k, a, b(k = 0,表示求子数列[a, b]的和;k = 1,表示第 a 个数加b)。
数列从1开始计数。
输出格式
输出若干行数字,表示k=0 时,对应的子数列[a, b]的连续和。
数据范围
1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n,
数据保证在任何时候,数列中所有元素之和均在 int 范围内。
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
1
2
3
4
5
6
7
输出样例:
11
30
35
1
2
3
ans
#include <cstdio>
#include <iostream>
#include <algorithm>
const int N = 1e5 + 10;
struct segment_tree {
int l, r, weight;
} tree[N*4];
int n,m;
int w[N];
using namespace std;
void build_tree(int i, int l, int r) {
if (l == r) {
tree[i] = {l, r, w[l]};
return;
}
int mid = l + r >> 1;
//构建左子树
build_tree(i<<1, l, mid);
//构建右子树
build_tree(i<<1|1, mid + 1, r);
//节点权值
int sum = tree[i * 2].weight + tree[i * 2 + 1].weight;
//更新区间
tree[i] = {l,r,sum};
}
void pushup(int i){
tree[i].weight = tree[i<<1].weight + tree[i<<1|1].weight;
}
int query(int i,int l,int r){
//结点维护区间是目标区间的子集,直接返回权值
if(tree[i].l>=l&&tree[i].r<=r)return tree[i].weight;
int mid = tree[i].l + tree[i].r >>1;
int sum = 0;
if(l<=mid) sum += query(i<<1,l,r);
if(r>mid)sum+= query(i<<1|1,l,r);
return sum;
}
void modify(int i, int l, int r,int v)
{
if(tree[i].l>=l&&tree[i].r<=r) tree[i].weight+=v*(tree[i].r - tree[i].l+1);
else{
int mid = tree[i].l + tree[i].r >>1;
if(l<=mid) modify(i<<1,l,r,v);
if(r>mid) modify(i<<1|1,l,r,v);
pushup(i);
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
build_tree(1, 1, n);
int k, a, b;
while (m -- )
{
scanf("%d%d%d", &k, &a, &b);
if (k == 0) printf("%d\n", query(1, a, b));
else modify(1, a,a, b);
}
return 0;
}
感谢你的阅读,希望本文对你有所帮助。