目录
1、对称加密
2、非对称加密
3、如何分配对称密钥?
4、如何分配非对称密钥?
1、对称加密
所谓对称加密,就是指加密密钥与解密密钥都使用相同的密钥。如下图所示,通信双方使用的就是对称加密密钥。//代表:DES和AES
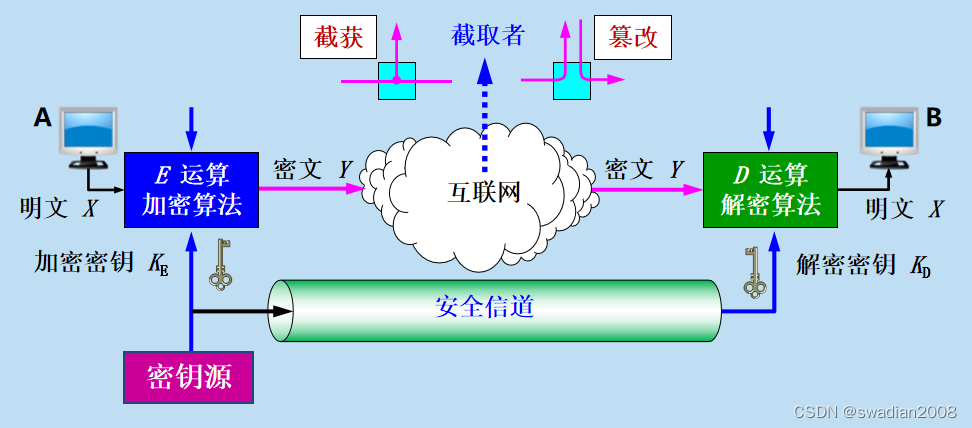
数据加密标准 DES(Data Encryption Standard) 属于对称密钥密码体制。它由 IBM 公司研制出,于 1977 年被美国定为联邦信息标准后,在国际上引起了极大的重视。ISO 曾将 DES 作为数据加密标准。
DES 是一种分组密码。在加密前,先对整个的明文进行分组。每一个组为 64 位长的二进制数据。然后对每一个 64 位二进制数据进行加密处理,产生一组 64 位密文数据。最后将各组密文串接起来,即得出整个的密文。使用的密钥占有 64 位(实际密钥长度为 56 位,外加 8 位用于奇偶校验)。
DES 的机密性仅取决于对密钥的保密,而算法是公开的。DES 的问题是它的密钥长度。56 位长的密钥意味着共有 种可能的密钥,也就是说,共有约 7.6 ×
种密钥。假设一台计算机 1 us 可执行一次 DES 加密,同时平均只需搜索密钥空间的一半即可找到密钥,那么破译 DES 要超过 1000 年。
然而芯片的发展出乎意料地快。不久,56 位 DES 已不再被认为是安全的。对于 DES 56 位密钥的问题,又提出了 三重DES(3DES) 的方案,把一个 64 位明文用一个密钥加密,再用另一个密钥解密,然后再使用第一个密钥加密,即
这里,X 是明文,Y 是密文,K1 和 K2 分别是第一个和第二个密钥, 表示用密钥 K1 进行 DES 加密,而
表示用密钥 K2 进行 DES 解密。//加密,解密,再加密
在 DES 之后,1997 年美国标准与技术协会(NIST),对一种新的加密标准即 高级加密标准 AES(Advanced Encryption Standard) 进行遴选,最后由两位年轻比利时学者 Joan Daemen 和 Vincent Rijmen 提交的 Rijndael算法 被选中,在 2001 年正式成为 NIST 的加密标准。在 2002 年成为美国政府加密标准。现在 AES 也是 ISO/IEC 18033-3 标准。
AES 也是一种分组密码,分组长度为 128 位。AES 有三种加密标准,其密钥分别为 128 位、192 位和 256 位,加密步骤相当复杂,运算速度比 3DES 快得多,且安全性也大大加强。在 2001 年,NIST 曾有一个大致的估计,就是假定有一台高速计算机,仅用 1 秒钟就能够破译 56 位的 DES,那么要破译 128 位的 AES,就需要 年!
2、非对称加密
非对称加密使用不同的加密密钥与解密密钥。也就是所谓的公钥密码体制。
公钥密码产生主要有两个方面的原因,一是由于对称密钥的密钥分配问题,二是对数字签名的需求。
在对称加密中,加解密的双方使用的是相同的密钥。但怎样才能做到这一点呢?
一种是事先约定,另一种是用信使来传送。在高度自动化的大型计算机网络中,用信使来传送密钥显然是不合适的。如果事先约定密钥,就会给密钥的管理和更换带来极大的不便。若使用高度安全的密钥分配中心 KDC(Key Distribution Center),也会使得网络成本增加。//密钥分配
对数字签名的强烈需要也是产生公钥加密的一个原因。在许多应用中,人们需要对纯数字的电子信息进行签名,表明该信息确实是某个特定的人产生的。//数字签名
对于公钥密码体制,目前最著名的是由美国三位科学家 Rivest, Shamir 和 Adleman 于1976 年提出并在 1978 年正式发表的 RSA 体制,它是一种基于数论中的大数分解问题的体制。
在公钥加密中,加密密钥 PK(Public Key 公钥) 是向公众公开的,而解密密钥 SK(Secret Key 私钥) 则是需要保密的。
公钥加密的加密和解密过程有如下特点:
- 首先,密钥对 生成器会为接收者 B 生成一对密钥:即公钥
和私钥
。
- 然后,发送者 A 用 B 的公钥
对明文 X 加密,得出密文 Y,发送给 B。
- 最后,B 接收到密文后,用自己的私钥
进行解密,恢复出明文。
//这个过程其实很好理解,就是如果要与B通信,就必须按照B给的方式对信息进行处理。处理后的信息,除了B,其他人都不能对这条信息进行解密。
//就比如你向你的朋友转账(通信),首先必须知道对方的账号(公钥),然后把钱转到对方的账户上(公钥加密),这样你的朋友使用密码就可以取得到你转账的钱(私钥解密)
下图,给出了使用公钥进行加密的过程:

需要注意的是,任何加密方法的安全性都取决于密钥的长度,以及攻破密文所需的计算量,而不是简单地取决于加密的方式(对称加密或非对称加密)。
3、如何分配对称密钥?
对称密钥分配存在以下两个问题:
- 第一,如果 n 个人中的每一个需要和其他 n-1 个人通信,就需要 n(n-1) 个密钥。但每两人共享一个密钥,因此密钥数是 n(n - 1)/2。这常称为
问题。如果 n 是个很大的数,所需要的密钥数量就非常大。//密码数量大
- 第二,通信的双方怎样才能安全地得到共享的密钥呢?正是因为网络不安全,所以才需要使用加密技术。但密钥又需要怎样传送呢?//网络不安全
目前常用的密钥分配方式是设立 密钥分配中心KDC(Key Distribution Center)。 KDC 是大家都信任的机构,其任务就是给需要进行秘密通信的用户临时分配一个会话密钥(仅使用一次)。
如下图,用户 A 和 B 都是 KDC 的登记用户。A 和 B 在 KDC 登记时就已经在 KDC 的服务器上安装了各自和 KDC 进行通信的 主密钥(master key) 和
。
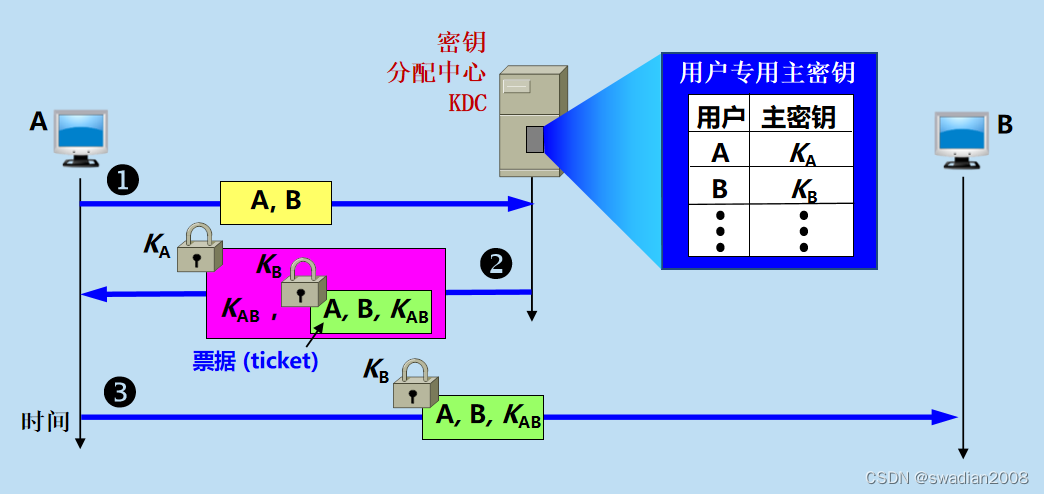
密钥分配分为三个步骤://单纯的对称密钥的分配比较麻烦
- 用户 A 向密钥分配中心 KDC 发送时用明文,说明想和用户 B 通信。在明文中给出了 A 和 B 在 KDC 登记的身份。
- KDC 用随机数产生“一次一密”的会话密钥
供 A 和 B 的这次会话使用,然后向 A 发送回答报文。这个回答报文用 A 的密钥
加密。这个报文中包含这次会话使用的密钥
和请 A 转给 B 的一个 票据(ticket),该票据包括 A 和 B 在 KDC 登记的身份,以及这次会话将要使用的密钥
。票据用 B 的密钥
加密,A 无法知道此票据的内容,因为 A 没有 B 的密钥
,当然 A 也不需要知道此票据的内容。
- 当 B 收到 A 转来的票据并使用自己的密钥
解密后,就知道 A 要和他通信,同时也知道 KDC 为这次和 A 通信所分配的会话密钥
。
此后,A 和 B 就可使用会话密钥进行这次通信了。需要注意的是,在网络上传送密钥时,都是经过加密的。解密用的密钥都不在网上传送。
4、如何分配非对称密钥?
我们都知道,使用非对称密钥时大家都各自保存有自己的私钥,然后把各自的公钥发布在网上。
但是,如何能确信获取的公钥真的就是对方的呢?
例如,A 和 B 都是公司。有个捣乱者给 A 发送邮件,声称自己是 B,要购买 A 生产的设备,货到付款,并给出了 B 的收货地址。邮件中还附上“B的公钥”(其实是捣乱者的公钥)。最后用捣乱者的私钥对邮件进行了签名。A 收到邮件后,就用邮件中给出的捣乱者的公钥,对邮件中的签名进行了鉴别,就误认为 B 真的是要购买设备。当 A 把生产的设备运到 B 的地址后,B 才知道被愚弄了!//B被冒充,A无法确认对方身份,因此交易会存在抵赖的可能性
现在流行的办法,这就是找一个可信任的第三方机构,给拥有公钥的实体发一个具有数字签名的数字证书(digital certificate)。数字证书就是对公钥与其对应的实体进行绑定(binding)的一个证明,因此它常称为公钥证书。这种签发证书的机构就叫作认证中心CA(Certification Authority),它由政府或知名公司出资建立(这样就可以得到大家的信任)。
每个证书中写有公钥及其拥有者的标识信息(人名、地址、电子邮件地址或 IP 地址等)。更重要的是,证书中有 CA 使用自己私钥的数字签名,这就是认证中心 CA 把 B 的未签名的证书进行散列函数运算,再用 CA 的私钥对散列值进行 D 运算(也就是对散列值进行签名)。这样就得到了 CA 的数字签名。把 CA 的数字签名和未签名的 B 的证书放在一起,就最后构成了已签名的 B 的数字证书。//CA使用自己的私钥对证书的散列值进行加密
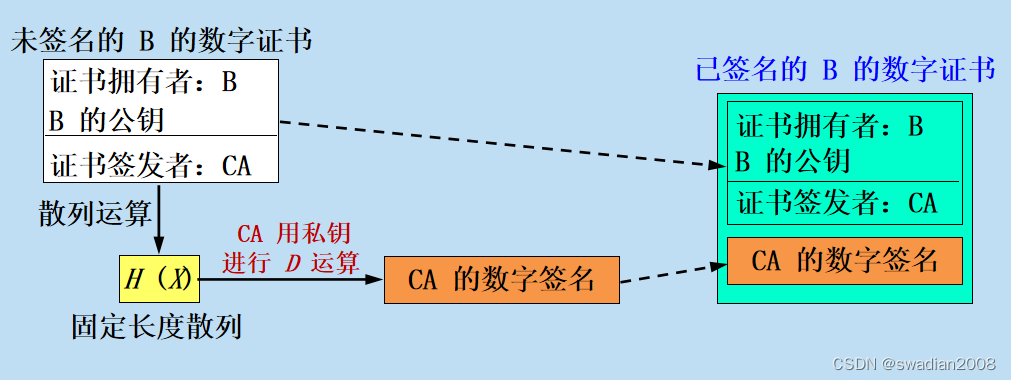
CA 证书无法伪造,任何用户都可从可信任的地方(如代表政府的报纸)获得认证中心 CA 的公钥,以验证证书的真伪。这种数字证书是公开的,不需要加密。
公司 A 拿到 B 的数字证书后,可以对 B 的数字证书的真实性进行核实。A 使用数字证书上给出的 CA 的公钥,对数字证书中 CA 的数字签名进行 E 运算,得出一个数值。再对 B 的数字证书(把 CA 的数字签名除外的部分)进行散列运算,又得出一个数值。比较这两个数值。若一致,则证明数字证书是真的。
关于数字证书的内容,X.509 规定了一个数字证书必须包括以下这些重要字段:
- X.509 协议的版本
- 数字证书名称及序列号
- 本数字证书所使用的签名算法
- 数字证书签发者的唯一标识符
- 数字证书的有效期(有效期开始到结束的日期范围)
- 主体名(或主题名,公钥和数字证书拥有者的唯一标识符)
- 公钥(数字证书拥有者的公钥和使用算法的标识符,对应的私钥由证书拥有者保存)
至此,全文结束。