目录

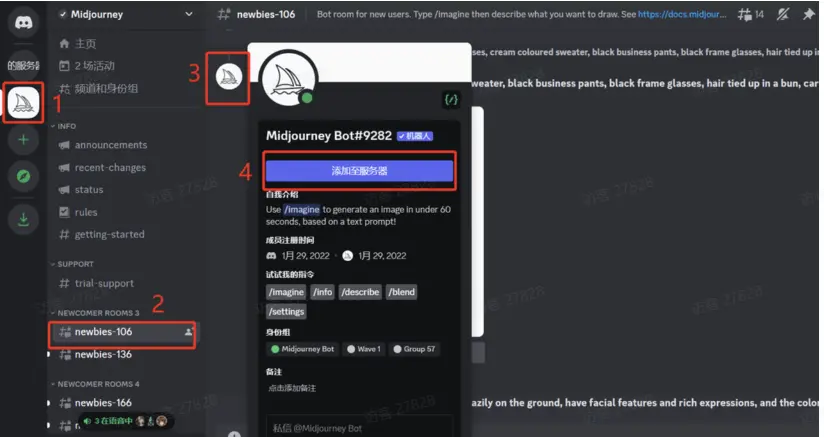
语法

说明

示例 

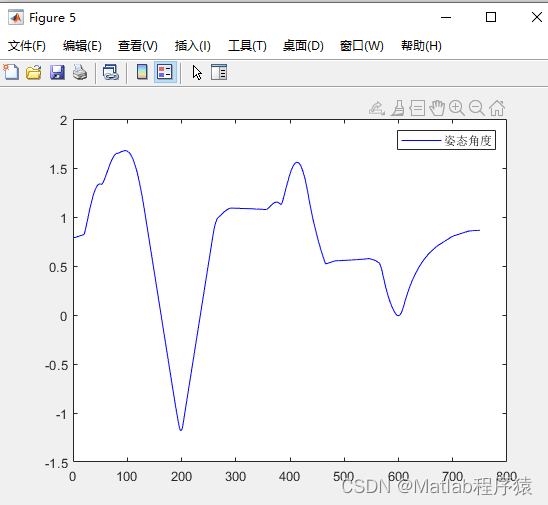
 二次多项式的根

四次多项式的根

提示

---

        roots函数的功能是求解多项式的根。

语法

r = roots(p)

说明

        r = roots(p) 以列向量的形式返回 p 表示的多项式的根。输入 p 是一个包含 n+1 多项式系数的向量，以 xn 系数开头。0 系数表示方程中不存在的中间幂。例如：p = [3 2 -2] 表示多项式：

        roots 函数对格式的多项式方程求解。包含带有非负指数的单一变量的多项式方程。

示例 

 二次多项式的根

        对方程 求解。创建一个向量，用它来代表多项式，然后计算多项式的根。

p = [3 -2 -4];
r = roots(p)
r = 2×1

    1.5352
   -0.8685

四次多项式的根

        对方程 x^4−1=0 求解。创建一个向量，用它来代表多项式，然后计算多项式的根。

p = [1 0 0 0 -1];
r = roots(p)
r = 4×1 complex

  -1.0000 + 0.0000i
   0.0000 + 1.0000i
   0.0000 - 1.0000i
   1.0000 + 0.0000i

参数说明：

        p— 多项式系数

提示

• 使用 poly 函数从其根 p = poly(r) 获取多项式。poly 函数是 roots 函数的逆函数。

• 使用 fzero 函数求非线性方程的根。roots 函数仅适用于多项式，fzero 函数则更广泛适用于不同类型的方程。