在机器学习和统计分类的领域中，Fisher判别（也称为Fisher线性判别分析）是一种非常重要的方法，旨在从数据中提取重要特征，以实现对样本的分类。即Fisher判别分析（Fisher Discriminant Analysis, FDA）是一种经典的线性分类方法，用于特征提取和数据降维，特别是在模式识别和机器学习领域中。这种方法由统计学家和生物学家罗纳德·费舍尔在1936年提出，至今仍广泛应用于各种数据分析任务中。

Fisher判别的基本思想

Fisher判别的核心思想是寻找一个线性组合的特征，使得通过这些特征变换后，不同类别的数据可以在新的维度上尽可能好地被区分开。具体来说，它尝试最大化类间差异（不同类别的数据点彼此远离）并最小化类内差异（同一类别的数据点尽可能聚集）。

Fisher判别的数学原理

Fisher判别的目标是找到一个线性投影，使得投影后，数据点在新的空间中能够实现最佳的类别分离。具体来说，它侧重于最大化类间差异（between-class variance）与类内差异（within-class variance）的比率。

Fisher判别分析（Fisher Discriminant Analysis, FDA）是一种经典的线性分类方法，用于特征提取和数据降维，特别是在模式识别和机器学习领域中。我们可以通过更详细的数学解释和步骤，来深入了解Fisher判别的具体实现和应用。

类内散度矩阵（Within-Class Scatter Matrix）

类内散度矩阵 ( S_W ) 描述了同一类别内的数据点如何分散。对于两个类别的情况，该矩阵定义为：

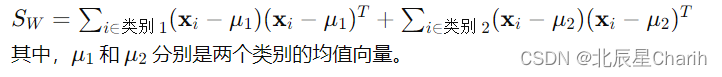
类间散度矩阵（Between-Class Scatter Matrix）

类间散度矩阵 ( S_B ) 描述了不同类别的均值之间的分散情况：

优化目标

Fisher判别分析的目标是找到一个方向向量w，使得投影到这个方向上的数据点最大化类间散度与类内散度的比率：

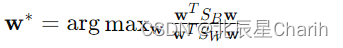
这个比率也被称为Rayleigh商，它的最优解可以通过求解广义特征值问题得到：

实现步骤

1. 计算均值向量：对每个类别，计算其所有样本点的均值向量。
2. 构建散度矩阵：根据上述公式计算类内散度矩阵和类间散度矩阵。
3. 求解特征值问题：解上述广义特征值问题，找到最大化类间散度和类内散度比的方向。
4. 数据投影：将数据投影到找到的方向向量上，进行分类或降维。

Fisher判别是如何工作的？

1. 计算类内和类间散度矩阵：类内散度矩阵描述了同一类别中数据点的分散程度，而类间散度矩阵描述了不同类别之间的分散程度。
2. 求解特征向量和特征值：Fisher判别分析的关键在于求解一个最优化问题，即找到能够最大化类间散度与类内散度比例的方向。这通常通过求解特定矩阵的特征值和特征向量来完成。
3. 降维和投影：通过这些特征向量，数据可以被投影到较低维度的空间中，同时保持类别之间尽可能的区分度。

应用示例

Fisher判别在许多实际问题中都有应用，例如：

• 人脸识别：通过提取人脸图片中最重要的特征，以区分不同的个人。
• 医学诊断：帮助从复杂的医疗数据中区分健康状况或疾病类型。
• 市场研究：分析消费者行为，区分不同的消费者群体。

优点与局限

优点：

• 简单高效：Fisher判别分析在理论上和计算上都相对简单。
• 适用性广：适用于大多数需要特征降维和分类的场景。

局限：

• 线性假设：假设数据是线性可分的，对于非线性数据可能需要进行转换或采用其他方法。
• 对异常值敏感：异常值可能会对计算结果造成较大影响。

应用考虑

虽然Fisher判别分析在理论上非常优雅，它仍有一些实际应用中的限制。例如，当类内散度矩阵 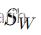接近奇异或非满秩时（可能因为样本数量小于特征数量），直接求解可能会有问题。在这种情况下，可能需要先进行PCA降维或添加正则化项以稳定计算。

此外，Fisher判别分析假设数据是线性可分的，对于非线性分布的数据可能表现不佳。针对这种情况，可以考虑使用核技巧的非线性扩展，即核Fisher判别分分析（Kernel Fisher Discriminant Analysis, KFDA），这种方法允许在原始数据被映射到一个更高维的空间中进行线性分析，从而处理那些在原始空间中非线性可分的情形。

分析（Kernel Fisher Discriminant Analysis, KFDA），这种方法允许在原始数据被映射到一个更高维的空间中进行线性分析，从而处理那些在原始空间中非线性可分的情形。

核Fisher判别分析

核Fisher判别分析通过引入核函数，能够处理复杂的非线性数据结构，使得Fisher判别分析的应用范围得到大幅扩展。核方法的基本思想是通过一个非线性映射将原始数据映射到一个高维特征空间，在这个新空间中数据的分布可能是线性可分的。

核函数

常用的核函数包括：

• 线性核：不增加非线性，保持数据的原始形态。
• 多项式核：通过增加原始特征的高次项来增加数据的维度，适合处理形式更为复杂的数据分布。
• 径向基函数（RBF）核：也称为高斯核，它可以映射出无限维的特征空间，非常适合处理那些在原始空间中难以线性分离的数据。

实现步骤

1. 选择核函数：根据数据的特性选择合适的核函数。
2. 计算核矩阵：核矩阵中的每个元素是数据点之间通过核函数计算得到的结果，它反映了映射到高维空间后的内积。
3. 求解广义特征值问题：在核空间中构造类内散度矩阵和类间散度矩阵，并求解相应的广义特征值问题，找到最优的投影方向。
4. 数据投影和分类：将数据通过核函数映射到高维空间后，根据求得的特征向量进行投影，再进行分类。

核Fisher判别的应用示例和挑战

核Fisher判别分析在图像识别、语音识别和生物信息学等多个领域显示了其强大的性能。例如，在人脸识别任务中，通过使用RBF核，可以有效地处理由于光照、表情和姿势变化带来的复杂变异。

尽管核方法增加了Fisher判别分析的灵活性，但也引入了一些挑战，如：

• 模型选择和超参数调优：核函数的选择和参数设置（如RBF核的宽度）对模型的性能有显著影响。
• 计算成本：尤其是在大规模数据集上，核矩阵的计算和存储可能非常昂贵。
• 过拟合问题：高维特征空间可能导致模型过于复杂，从而容易过拟合。

结论

尽管Fisher判别是一个历史悠久的方法，但它因其理论的完整性和实用性而持续受到青睐。在现代数据科学的许多方面，从自然语言处理到图像识别，Fisher判别分析都扮演着重要的角色。Fisher判别分析无论是在其原始形式还是通过核技巧扩展后的形式，都是机器学习和统计分类中非常有用的工具。理解并正确应用这些技术，可以显著提高模型的分类效果，特别是在需要强大特征提取能力的应用场景中。对于希望深入理解数据特征和进行有效分类的研究者和工程师来说，掌握Fisher判别分析无疑是宝贵的技能之一。