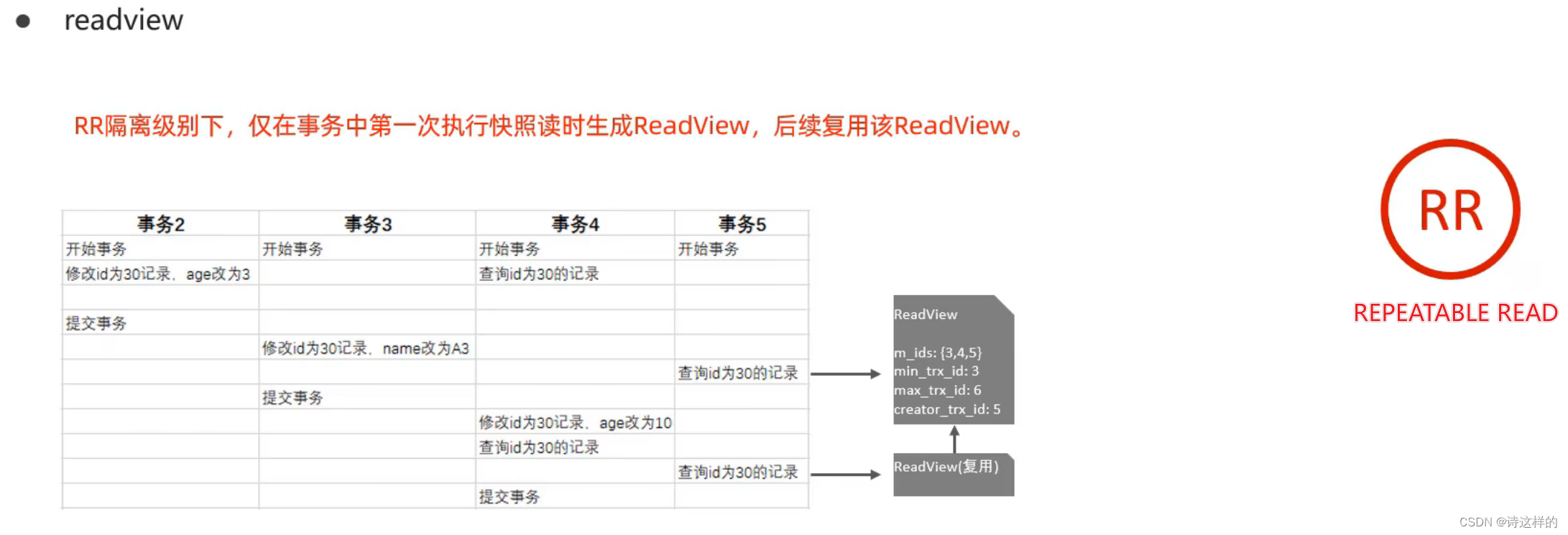
Taxi Cab Scheme

题意

有一张边长不超过 $200$ 的网格图，有若干个乘客，
乘客 $i$ 的需求是：$hh:mm,(a,b),(c,d)$，意为他需要在 $hh时mm分$（或更早）从点 $(a,b)$ 出发，终点为 $(c,d)$
图上两点的距离就是 曼哈顿距离

现在我们需要使用一些出租车来满足这些乘客的需求，问最少需要几台车？

一台车必须在当前要接送的顾客要求的时间更早到达起点（起码$1min$），才能接送成功

思路

最优的情况是只用一台车，那么这台车每次接完当前顾客，它都需要从这个顾客的终点移动到下一个顾客的起点，并且最终到达的时间必须比下一个顾客的要求时间早

那么我们不妨先预处理一下每个乘客的结束时间，存储一下起始时间，并将所有时间转换成 分钟制，便于比较

如果送完了当前顾客 $i$，还能接送下一个顾客 $j$，那么我们可以连边：$i\to j$，表示这个传递关系

那么我们 $O(n^2)$ 连完边后，从结果出发，如果我们选择了若干辆出租车，每辆出租车按一条路径这样搜索下去，直到不能搜素为止，最终每一个点都被访问了一次

可以发现：关键就是怎么选取这个起始点？也就是选择哪些点作为第一批送走的顾客

我们再进一步想：如果我们选择的集合里面，有两个点，其中一个点可以被另一个点搜索到，也就是说这个点是多余的，那么这个点可以删去
那么我们可以得出结论：最终选择的点集，一定是两两不可达的，等价于集合内没有边，
等价于集合是独立集

我们可以在这张二分图上跑最大匹配，那么最终残余网络上，右点还有容量的点就是起点，左点还有容量的点就是终点，由于已经跑出了最大流量，所以残余网络不会变得更小，因此这个起点集就是最小的

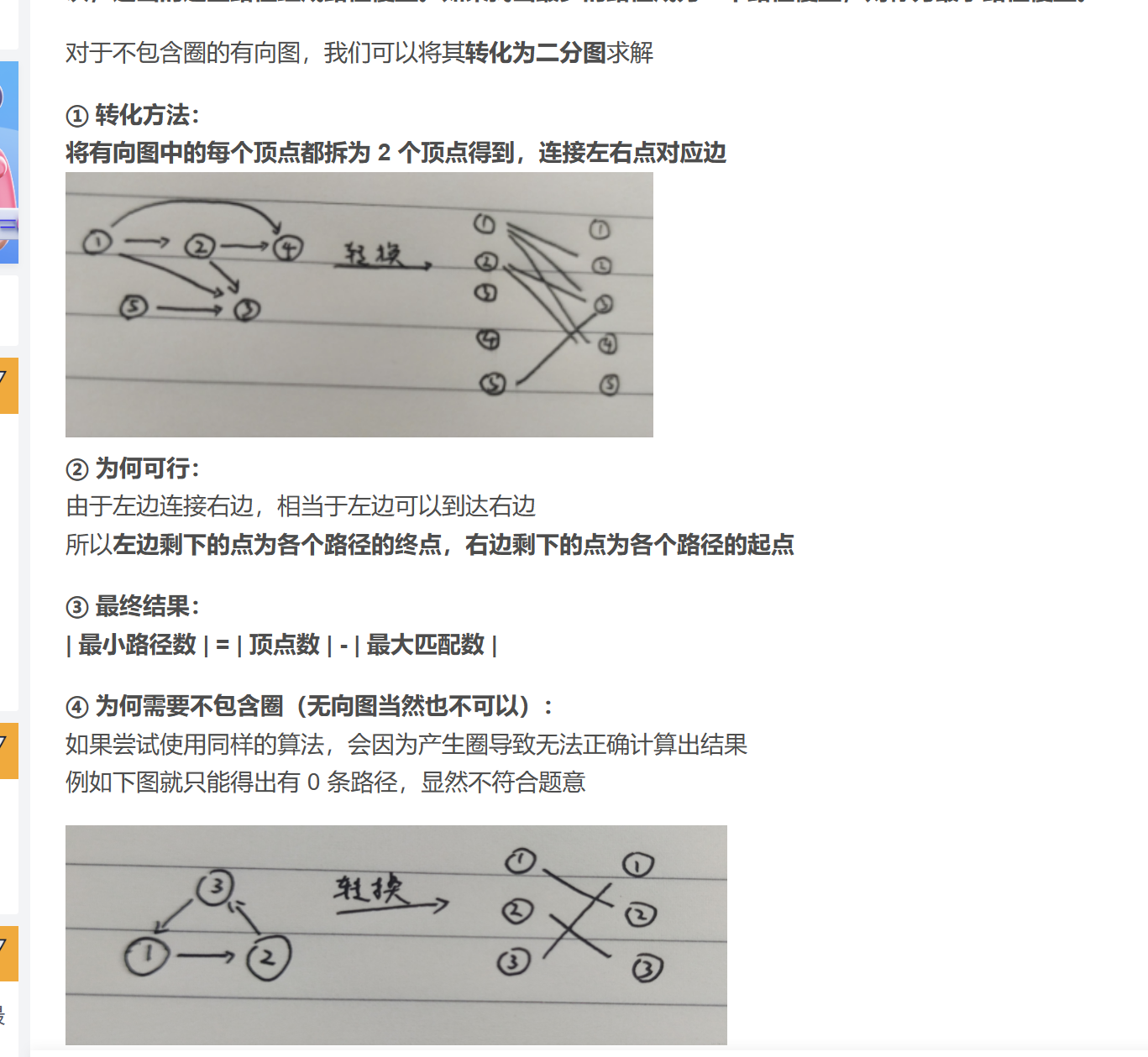
部分思路参考自：最小路径覆盖详解 超级详细

#include<bits/stdc++.h>
#define fore(i,l,r)	for(int i=(int)(l);i<(int)(r);++i)
#define fi first
#define se second
#define endl '\n'
#define ull unsigned long long
#define ALL(v) v.begin(), v.end()
#define Debug(x, ed) std::cerr << #x << " = " << x << ed;

const int INF=0x3f3f3f3f;
const long long INFLL=1e18;

typedef long long ll;

std::vector<std::vector<int>> g;
std::vector<int> match;
std::vector<bool> used;

bool dfs(int u){
    for(auto v : g[u])
        if(!used[v]){
            used[v] = true;
            if(match[v] == -1 || dfs(match[v])){
                match[v] = u;
                return true;
            }
        }
    return false;
}

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    int t;
    std::cin >> t;
    while(t--){
        int n;
        std::cin >> n;
        g.assign(n, std::vector<int>());
        match.assign(n, -1);

        std::vector<std::pair<int, int>> p(n); //source pos
        std::vector<std::pair<int, int>> pe(n); //end pos
        std::vector<std::pair<int, int>> time(n); //beg, end
        fore(i, 0, n){
            std::string s;
            std::cin >> s >> p[i].fi >> p[i].se;
            int x, y;
            std::cin >> x >> y;
            pe[i] = {x, y};
            int dis = std::abs(p[i].fi - x) + std::abs(p[i].se - y);
            int t0 = atoi(s.substr(0, 2).c_str()) * 60 + atoi(s.substr(3).c_str());
            time[i] = {t0, t0 + dis};
        } 

        fore(i, 0, n)
            fore(j, i + 1, n){
                auto [x1, y1] = pe[i];
                auto [x2, y2] = p[j];
                int dis = std::abs(x1 - x2) + std::abs(y1 - y2);
                if(time[i].se + dis < time[j].fi){
                    g[i].push_back(j);
                }
            }

        int cnt = 0;
        fore(i, 0, n){
            used.assign(n, false);
            cnt += dfs(i);
        }

        std::cout << n - cnt << endl;
    }
    return 0;
}