《剑指 Offer》专项突破版 - 面试题 113、114 和 115 : 详解拓扑排序（C++ 实现）

前言

面试题 113 : 课程顺序

面试题 114 : 外星文字典

面试题 115 : 重建序列

前言

拓扑排序是指对一个有向无环图的节点进行排序之后得到的序列。如果存在一条从节点 A 指向节点 B 的边，那么在拓扑排序的序列中节点 A 出现在节点 B 的前面。一个有向无环图可以有一个或多个拓扑排序序列，但无向图或有环的有向图不存在拓扑排序。

在讨论有向无环图拓扑排序算法之前先介绍两个概念：入度和出度。节点 v 的入度指的是以节点 v 为终点的边的数目，而节点 v 的出度是指以节点 v 为起点的边的数目。例如，在下图 (a) 的有向图中，节点 2 的入度是 1，出度是 2。

一种常用的拓扑排序算法是每次从有向无环图中取出一个入度为 0 的节点添加到拓扑排序序列之中，然后删除该节点及所有以它为起点的边。重复这个步骤，直到图为空或图中不存在入度为 0 的节点。如果最终图为空，那么图是有向无环图，此时就找到了该图的一个拓扑排序序列；如果最终图不为空并且已经不存在入度为 0 的节点，那么图中一定有环。

下面对下图 (a) 中的图进行拓扑排序，该图中节点 1 的入度为 0，将该节点添加到拓扑排序序列中，并删除该节点及所有以该节点为起点的边，如下图 (b) 所示。接下来重复这个步骤，依次找到入度为 0 的节点 2、节点 3、节点 4、节点 5，如下图 (c)、(d)、(e) 所示，在先后删除这些节点之后图为空。因此，下图 (a) 中的图是有向无环图，它的拓扑排序序列为 [1, 2, 3, 4, 5]。

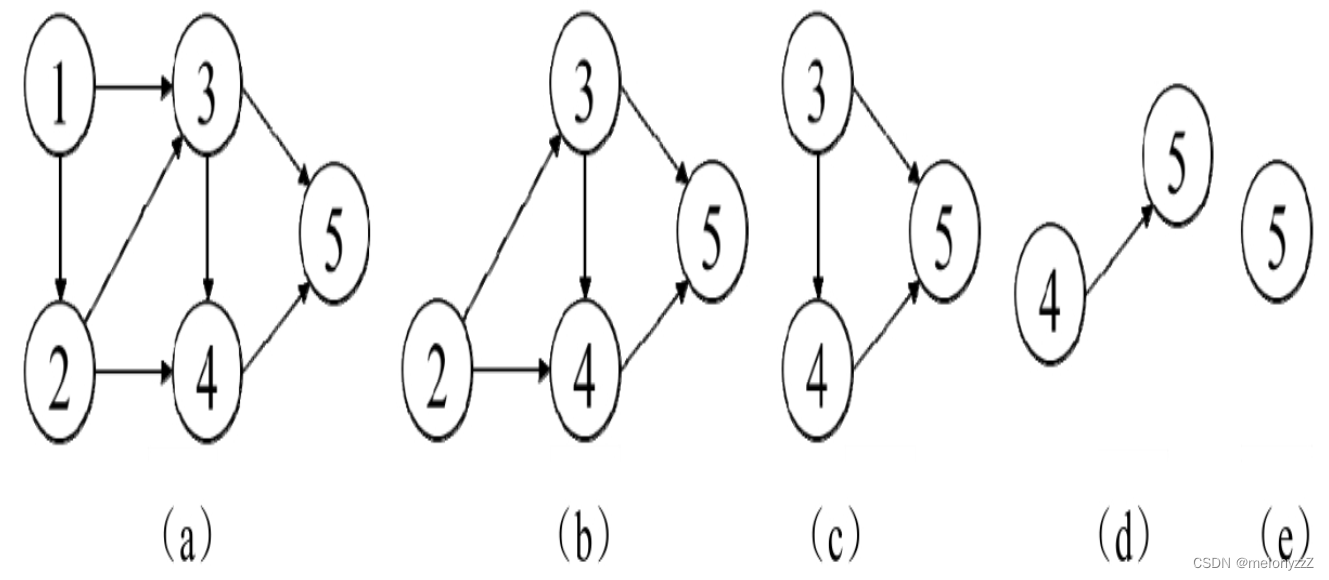
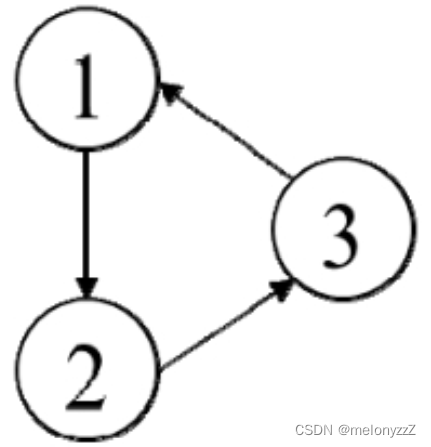
上述算法也可以用来判断一个有向图是否有环。如果执行上述步骤最终得到一个非空的图，并且图中所有节点的入度都大于 0，那么该图一定包含环。例如，下图中的有向图中的 3 个节点的入度都为 1，它们形成一个环。

面试题 113 : 课程顺序

题目：

n 门课程的编号为 0 ~ n - 1。输入一个数组 prerequisites，它的每个元素 prerequisites[i] 表示两门课程的先修顺序。如果 prerequisites[i] = [ $a_i, b_i$ ]，那么必须先修完 $b_i$ 才能修 $a_i$ 。请根据总课程数 n 和表示先修顺序的 prerequisites 得出一个可行的修课序列。如果有多个可行的修课序列，则输出任意一个可行的序列；如果没有可行的修课序列，则输出空序列。

例如，总共有 4 门课程，先修顺序 prerequisites 为 [[1, 0], [2, 0], [3, 1], [3, 2]]，一个可行的修课序列是 0->2->1->3。

分析：

将课程看成图中的节点，如果两门课程存在先修顺序那么它们在图中对应的节点之间存在一条从先修课程到后修课程的边，因此这是一个有向图。例如，可以根据先修顺序 prerequisites 为 [[1, 0], [2, 0], [3, 1], [3, 2]] 构建出如下图所示的有向图。例如，课程先修顺序 [1, 0] 对应在图中就有一条从节点 0 到节点 1 的边。

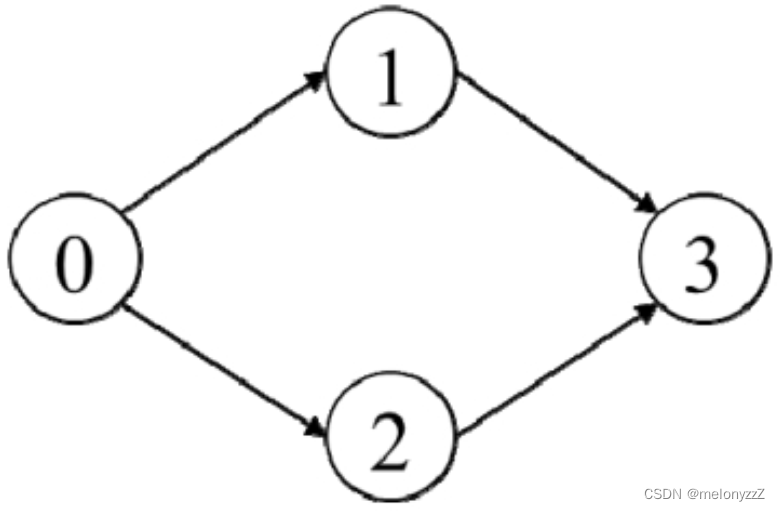
可行的修课序列实际上是图的拓扑排序序列。图中的每条边都是从先修课程指向后修课程，而拓扑排序能够保证任意一条边的起始节点一定排在终止节点的前面，因此拓扑排序得到的序列与先修顺序一定不会存在冲突，于是这个问题转变成如何求有向图的拓扑排序序列。

对有向图进行拓扑排序的算法是每次找出一个入度为 0 的节点添加到序列中，然后删除该节点及所有以该节点为起点的边。重复这个过程，直到图为空或图中不存在入度为 0 的节点。

代码实现：

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        unordered_map<int, vector<int>> graph;
        for (int i = 0; i < numCourses; ++i)
        {
            graph.insert({ i, vector<int>() });
        }

        vector<int> inDegrees(numCourses, 0);
        for (vector<int>& prerequisite : prerequisites)
        {
            graph[prerequisite[1]].push_back(prerequisite[0]);
            ++inDegrees[prerequisite[0]];
        }

        queue<int> q;
        for (int i = 0; i < numCourses; ++i)
        {
            if (inDegrees[i] == 0)
                q.push(i);
        }

        vector<int> order;
        while (!q.empty())
        {
            int course = q.front();
            q.pop();
            order.push_back(course);
            for (int next : graph[course])
            {
                --inDegrees[next];
                if (inDegrees[next] == 0)
                    q.push(next);
            }
        }
        return order.size() == numCourses ? order : vector<int>();
    }
};

上述代码先根据先修顺序构建出有向图 graph，graph 用一个 unordered_map 表示邻接表，它的键是先修课程，它的值是必须在键对应的课程之后学习的所有课程。同时，将每个节点的入度保存到数组 inDegrees 中，inDegrees[i] 表示节点 i 的入度。

接下来用广度优先搜索算法实现拓扑排序。队列中保存的是入度为 0 的节点。每次从队列中取出一个节点，将该节点添加到拓扑排序序列中，然后找到该课程的后修课程并将它们的节点的入度减 1，这相当于删除从先修课程到后修课程的边。如果发现新的入度为 0 的节点，则将其添加到队列中。重复这个过程直到队列为空，此时要么图中所有节点都已经访问完毕，已经得到了完整的拓扑排序序列；要么剩下的还没有搜索到的节点形成一个环，已经不存在入度为 0 的节点。

面试题 114 : 外星文字典

题目：

一种外星语言的字母都是英文字母，但字母的顺序未知。给定该语言排序的单词列表，请推测可能的字母顺序。如果有多个可能的顺序，则返回任意一个。如果没有满足条件的字母顺序，则返回空字符串。例如，如果输入排序的单词列表为 ["ac", "ab", "bc", "zc", "zb"]，那么一个可能的字母顺序是 "acbz"。

分析：

这个题目比较难。如果在面试中遇到比较难的问题，比较有效地分析、解决问题的思路是从具体的例子中总结出解题规律。

在排序的单词列表 ["ac", "ab", "bc", "zc", "zb"] 中，一共出现了 4 个字母，即 'a'、'b'、'c' 和 'z'。需要根据单词的顺序确定这 4 个字母的顺序。由于 "ac" 排在 "ab" 的前面，因此字母 'c' 应该排在字母 'b' 的前面（即 'c' < 'b'），这是因为这两个单词的第 1 个字母相同，第 2 个字母不同，那么它们的第 2 个字母的顺序确定了两个单词的顺序。接下来两个相邻的单词是 "ab" 和 "bc"，它们的第 1 个字母就不同，那么它们的顺序由第 1 个字母确定，所以 'a' < 'b'。类似地，可以根据 "bc" 排在 "zc" 的前面得知 'b' < 'z'，根据 "zc" 排在 "zb" 的前面得知 'c' < 'b'。

由比较排序的单词列表中两两相邻的单词可知 'c' < 'b'、'a' < 'b' 和 'b' < 'z'，现在需要找出一个包含 4 个字母的字母序列满足已知的 3 个字母的大小顺序。这看起来就是一个关于拓扑排序的问题，可以将每个字母看成图中的一个节点，如果已知两个字母的大小关系，那么图中就有一条从较小的字母指向较大的字母的边。根据字母的大小关系 'c' < 'b'、'a' < 'b' 和 'b' < 'z' 构建出的有向图如下图所示，该有向图有两个拓扑排序序列，"acbz" 和 "cabz"，相应地输入的单词列表就有两个可能的字母顺序。

如果能够得出该有向图的拓扑排序序列，那么任意一条边的起始节点（较小的字母）在拓扑排序序列中一定出现在终止节点（较大的字母）的前面。因此，这个问题实质上是一个关于拓扑排序的问题。

代码实现：

class Solution {
public:
    string alienOrder(vector<string>& words) {
        unordered_map<char, unordered_set<char>> graph;
        unordered_map<char, int> inDegrees;
        for (string& word : words)
        {
            for (char ch : word)
            {
                if (!graph.count(ch))
                {
                    graph.insert({ ch, unordered_set<char>() });
                    inDegrees.insert({ ch, 0 });
                }
            }
        }

        for (int i = 0; i < words.size() - 1; ++i)
        {
            string w1 = words[i], w2 = words[i + 1];
            int j = 0;
            while (j < w1.size() && j < w2.size())
            {
                char ch1 = w1[j], ch2 = w2[j];
                if (ch1 != ch2)
                {
                    if (!graph[ch1].count(ch2))
                    {
                        graph[ch1].insert(ch2);
                        ++inDegrees[ch2];
                    }
                    break;
                }
                ++j;
            }

            if (j < w1.size() && j == w2.size())
                return "";
        }

        queue<char> q;
        for (auto& kv : inDegrees)
        {
            if (kv.second == 0)
                q.push(kv.first);
        }

        string order;
        while (!q.empty())
        {
            char ch = q.front();
            q.pop();
            order.push_back(ch);
            for (char next : graph[ch])
            {
                --inDegrees[next];
                if (inDegrees[next] == 0)
                    q.push(next);
            }
        }
        return order.size() == graph.size() ? order : "";
    }
};

在上述代码中，图用 unordered_map 类型的变量 graph 以邻接表的形式表示。与某节点相邻的节点（即比某字母大的节点）则用一个 unordered_set 保存（在比较排序的单词列表中两两相邻的单词时可能得到相同的两个字母的大小关系，需要快速判断图中是否存在这样的一条边，所以不使用 vector，而是 unordered_set）。unordered_map 类型的变量 inDegrees 保存每个节点的入度（这里也不适合使用 vector）。代码一开始找出单词列表 words 中出现的所有字母并做相应的初始化。

接下来比较单词列表 words 中两两相邻的单词，从头找出第 1 组不同的两个字母，在图中添加一条从较小的字母（ch1）指向较大的字母（ch2）的边。

这里有一类特殊的输入需要特别注意。如果排在后面的单词是排在前面的单词的前缀，那么无论什么样的字母顺序都是不可能的。例如，如果排序的单词列表是 ["abc", "ab"]，不管是什么样的字母顺序，"abc" 都不可能排在 "ab" 的前面，因此这是一个无效的输入，此时可以直接返回空字符串表示无效的字母顺序。

面试题 115 : 重建序列

题目：

长度为 n 的数组 org 是数字 1 ~ n 的一个排列，seqs 是若干序列，请判断数组 org 是否为可以由 seqs 重建的唯一序列。重建的序列是指 seqs 所有序列的最短公共超序列，即 seqs 中的任意序列都是该序列的子序列。

例如，如果数组 org 为 [4, 1, 5, 2, 6, 3]，而 seqs 为 [[5, 2, 6, 3], [4, 1, 5, 2]]，因为用 [[5, 2, 6, 3], [4, 1, 5, 2]] 可以重建出唯一的序列 [4, 1, 5, 2, 6, 3]，所以返回 true。如果数组 org 为 [1, 2, 3]，而 seqs 为 [[1, 2], [1, 3]]，因为用 [[1, 2], [1, 3]] 可以重建出两个序列，[1, 2, 3] 或 [1, 3, 2]，所以返回 false。

分析：

超序列和子序列是两个相对的概念。如果序列 A 中的所有元素按照先后的顺序都在序列 B 中出现，那么序列 A 是序列 B 的子序列，序列 B 是序列 A 的超序列。

按照题目的要求，如果在 seqs 的某个序列中数字 i 出现在数字 j 的前面，那么由 seqs 重建的序列中数字 i 一定也要出现在数字 j 的前面。也就是说，重建序列的数字顺序由 seqs 的所有序列定义。

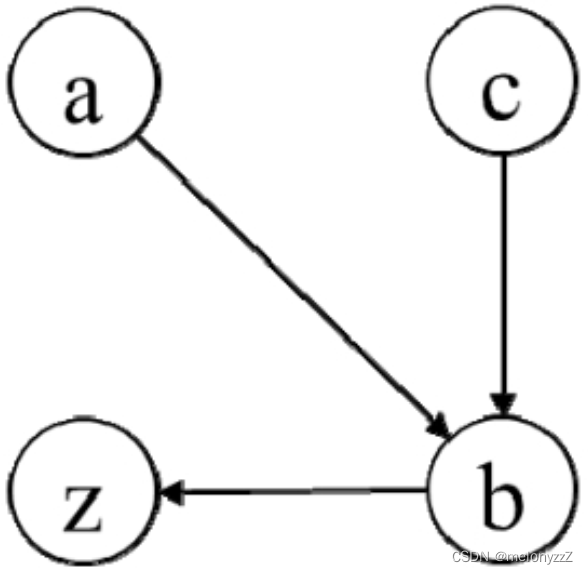
可以将 seqs 中每个序列的每个数字看成图中的一个节点，两个相邻的数字之间有一条从前面数字指向后面数字的边。例如，由 [[5, 2, 6, 3], [4, 1, 5, 2]] 构建的有向图如下图 (a) 所示，由 [[1, 2], [1, 3]] 构建的有向图如下图 (b) 所示。

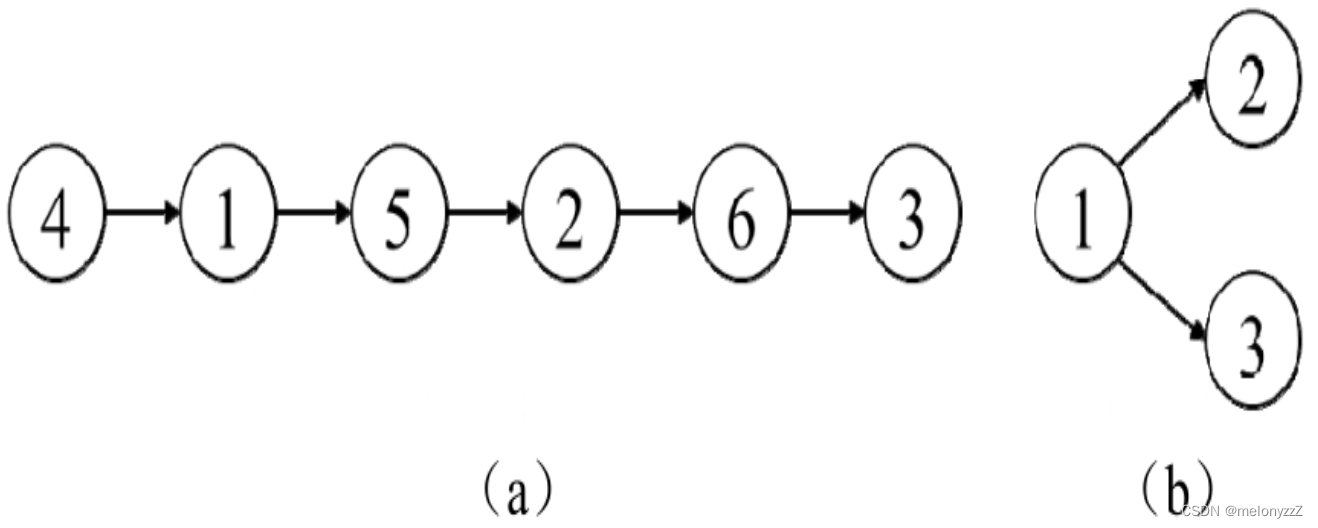
如果得到的是有向图的拓扑排序序列，那么任意一条边的起始节点在拓扑排序序列中一定位于终止节点的前面。因此，由 seqs 重建的序列就是由 seqs 构建的有向图的拓扑排序的序列。这个问题就转变成判断一个有向图的拓扑排序序列是否唯一。

上图 (a) 中的有向图的拓扑排序序列是唯一的，其中，节点 4 是图中唯一一个入度为 0 的节点，删除该节点和以该节点为起始节点的边之后节点 1 是下一个唯一的入度为 0 的节点，重复这个过程直到图为空，就可以得到唯一的拓扑排序序列 [4, 1, 5, 2, 6, 3]。

而上图 (b) 则不然，其中，节点 1 是图中唯一一个入度为 0 的节点，删除该节点和以它为起始节点的边之后，节点 2 和节点 3 的入度都为 0，因此这个有向图有两个拓扑排序序列，分别为 [1, 2, 3] 和 [1, 3, 2]。

代码实现：

class Solution {
public:
    bool sequenceReconstruction(vector<int>& nums, vector<vector<int>>& sequences) {
        unordered_map<int, unordered_set<int>> graph;
        unordered_map<int, int> inDegrees;
        for (vector<int>& sequence : sequences)
        {
            for (int i = 0; i < sequence.size(); ++i)
            {
                if (sequence[i] < 1 || sequence[i] > nums.size())
                    return false;
                
                if (!graph.count(sequence[i]))
                {
                    graph.insert({ sequence[i], unordered_set<int>() });
                    inDegrees.insert({ sequence[i], 0 });
                }
            }

            for (int i = 1; i < sequence.size(); ++i)
            {
                int prev = sequence[i - 1], cur = sequence[i];
                if (!graph[prev].count(cur))
                {
                    graph[prev].insert(cur);
                    ++inDegrees[cur];
                }
            }
        }

        queue<int> q;
        for (auto& kv : inDegrees)
        {
            if (kv.second == 0)
                q.push(kv.first);
        }

        vector<int> reconstruction;
        while (q.size() == 1)
        {
            int num = q.front();
            q.pop();
            reconstruction.push_back(num);
            for (int next : graph[num])
            {
                --inDegrees[next];
                if (inDegrees[next] == 0)
                    q.push(next);
            }
        }

        return reconstruction == nums;
    }
};

上述代码首先根据序列列表 seqs 构建有向图，有向图以邻接表的形式用 unordered_map 类型的 graph 保存。同时，统计每个节点的入度并保存到另一个 unordered_map 类型的 inDegrees 中。

接下来对构建的有向图按照广度优先搜索进行拓扑排序。队列 q 中保存的是入度为 0 的节点。每次从队列中取出一个节点添加到拓扑排序序列中，然后将所有与该节点相邻的节点的入度减 1（相当于删除所有以该节点为起始节点的边），如果发现有新的入度为 0 的节点则添加到队列之中。由于目标是判断图的拓扑排序序列是否唯一，而当某个时刻队列中的节点数目大于 1 时，就知道此时有多少个入度为 0 的节点，那么按照任意顺序排列这个入度为 0 的节点都能生成有效的拓扑排序序列，因此拓扑排序的序列不是唯一的。由此可知，上述代码只在队列的大小为 1 的时候重复添加入度为 0 的节点。