前言
这阵子一直在学数据结构,知识点消化地有点慢导致博客一直没写,现在总算是有时间歇下来补补前面落下的博客了。从现在起恢复周更,努努力一周两篇也不是梦……闲话少说,今天就让我们一起来认识栈和队列
1. 栈的介绍和使用
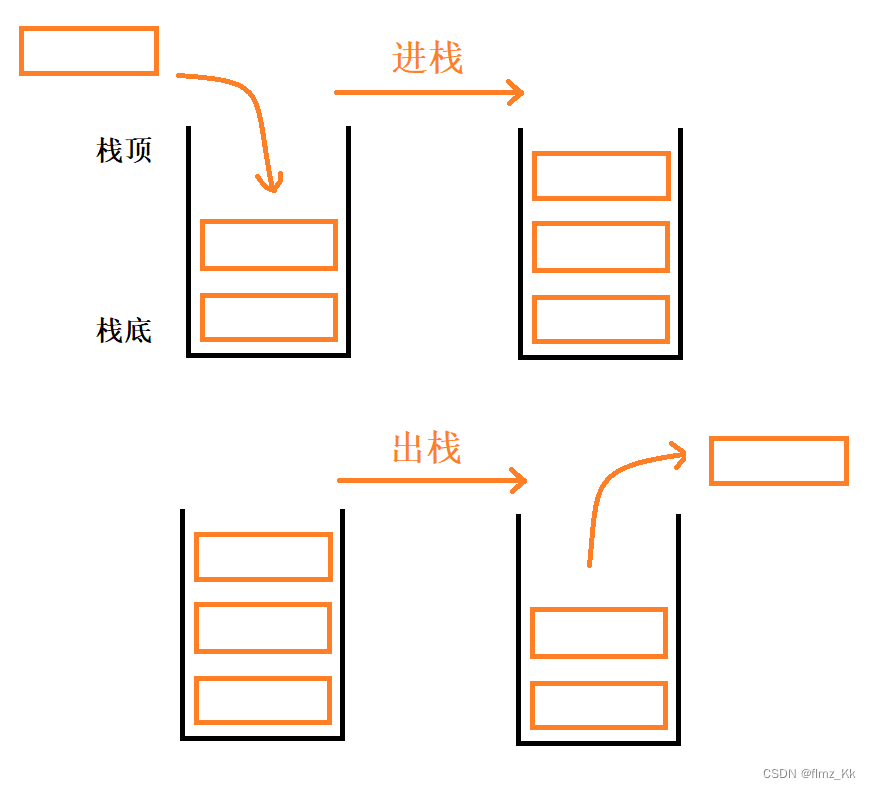
栈(stack)是一种特殊的线性表,它只允许先进后出,也就是只能在固定的一端进行插入和删除操作。上面的一端叫做栈顶,可以插入删除,下面的一端就叫做栈底。
压栈/入栈/进栈:即从栈顶添加数据
出栈:即数据在栈顶弹出
栈的原则是:先进后出——就像子弹上膛,弹匣最先压进的子弹最后射出
1.1 语法格式
Stack类位于java.util包当中,我们在使用前要记得导包
import java.util.Stack;
Stack<E> stack = new Stack<>();又因为Stack实现了List接口,所以我们也可以用接口来引用Satck对象,要记得List类也需要导包
import java.util.List;
import java.util.ArrayList;
List<E> stack = new Stack<>();对于两种stack的创建,我更推荐第二种,因为List接口的方法更多,而且Stack我们现在用的比较少,不常用了
注:我们在这里介绍的是Stack的原生方法,也就是用第一种方法创建的,并非是接口的方法
1.2 入栈
E push(E e):将e入栈,并且返回e,e以及返回值的类型都为E
Stack<Integer> stack = new Stack<>();
stack.push(12);
stack.push(23);
stack.push(34);
System.out.println(stack);因为Stack已经重写了toString方法,所以我们还可以直接打印list,运行结果如下
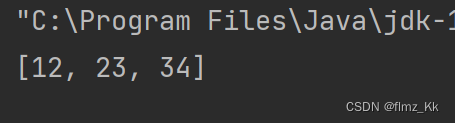
1.3 出栈
E pop():将栈顶元素出栈并返回,它会删除栈顶元素
E peek():获取栈顶元素,它并不会删除栈顶元素
Stack<Integer> stack = new Stack<>();
stack.push(12);
stack.push(23);
stack.push(34);
System.out.println(stack);
stack.pop();//34被删除
Integer p1 = stack.peek();
System.out.println(p1);//23
System.out.println(stack);我们用Stack()先创建了一个空栈,然后连续三个push(),栈内元素从下往上是:12、23、34,接下就pop(),删除栈顶元素34,接着在创建一个p1来接收peek()的值,打印p1,最后在打印stack整个栈。运行结果如下:
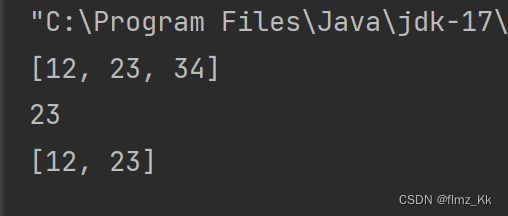
1.4 栈的空间
int size():获取栈的大小
boolean empty():检测栈是否为空
*boolean isEmpty():也是判空(是从Collection继承而来的)
Stack<Integer> stack = new Stack<>();
stack.push(12);
stack.push(23);
stack.push(34);
int size = stack.size();
System.out.println(size);
boolean flag1 = stack.empty();
System.out.println(flag1);
//继承来的
boolean flag2 = stack.isEmpty();
System.out.println(flag2);2. 栈的模拟实现
栈是一种特殊的顺序表,它始终遵循先进后出的原则。因此我们可以用数组来模拟实现,同时我们还可以设置一个size值,它可以用来表示当前存放数据的个数,也就是栈的大小;我们还可以用它来表示当前将要存放数据的下标
import java.util.Arrays;
public class MyStack {
int[] array;
int usedSize;
public MyStack(){
this.array = new int[10];
}
//入栈
public void push(int val) {
if (isFull()) {
//扩容
this.array = Arrays.copyOf(array,2*array.length);
}
array[usedSize] = val;
usedSize++;
}
//判满
public boolean isFull() {
return usedSize == array.length;
}
//出栈,删除栈顶元素
public int pop() {
if (isFull()) {
return -1;
}
int ret = array[usedSize-1];
usedSize--;
return ret;
}
//获得栈顶元素但不删除
public int peek() {
if (isFull()) {
return -1;
}
return array[usedSize-1];
}
//求栈的空间大小
public int size() {
return usedSize;
}
//判空
public boolean empty() {
return 0 == usedSize;
}
}
3. 栈的应用场景
括号匹配 —— 力扣 20. 有效的括号
分析:我们可以把想到的情况都列出来,以下四种情况中,只有第一种才是true,其余三种都是false
我们先创建一个空栈,然后遍历字符串s,遇到左括号就入栈,接着继续遍历,遇到右括号就用peek获得栈顶元素,然后跟右括号匹配。如果是一对的,就把左括号出栈,如果不是一队,就直接返回false。而且如果我们遍历完字符串s后,栈还不为空,就时情况三和情况四,直接返回false
具体代码
class Solution {
public boolean isValid(String s) {
//创建一个空栈
Stack<Character> stack = new Stack<>();
//遍历字符串s
for(int i = 0; i < s.length(); i++) {
把字符串s的元素一个个拆出来
char ch1 = s.charAt(i);
//如果为左括号,就入栈
if(ch1 == '(' || ch1 == '[' || ch1 == '{') {
stack.push(ch1);
} else {
//判断栈空不空,空则返回false
if(stack.empty()) {
return false;
}
else {
//当前ch1为右括号,那就先获取栈顶元素
char ch2 = stack.peek();
if((ch2 == '(' && ch1 == ')')
|| (ch2 == '{' && ch1 == '}')
|| (ch2 == '[' && ch1 == ']') ) {
//匹配成功,栈顶的左括号出栈
stack.pop();
} else {
//匹配失败,直接返回false
return false;
}
}
}
}
//字符串s遍历完了,直接用栈是否为空来当返回值
return stack.empty();
}
}逆波兰表达式 —— 力扣 150. 逆波兰表达式求值
在做这道题之前,我们先来讲一下什么是逆波兰表达式:
逆波兰表达式:也叫做后缀表达式,即运算符在操作数后面。我们平时所看到的表达式都是中缀表达式,就像 2 * (3 + 5),这个表达式我们看起来很简单,算起来也不难;但是对于计算机来说,它就读不懂这个表达式的意思,因此逆波兰表达式应运而生。
逆波兰表达式的格式非常奇怪,我们可以把中缀表达式转换成逆波兰表达式:就像 2 * (3 + 5),转换后就是 2 3 5 *+,是不是完全看不懂?看不懂就对了,因为这是专门给计算机看的。
我们还可以把中缀表达式转换成逆波兰表达式,这里有两种方法:
方法一:取巧法
- 把表达式从左到右加上括号(要按照先乘除后加减的顺序加)
- 把对应的运算符向右拉到对应的括号外面
方法二:使用栈,因为篇幅过长,此处不讲,有兴趣的可以在站内搜一下
讲了这么多,就是为了最后要怎么计算逆波兰表达式,没错,还是得用栈
思路:字符串数组tokens中既有数字又有符号,所以我们要额外写一个方法来判断,接着我们遍历字符串数组,一边遍历一边判断,当遇到数字时,就入栈;遇到就弹出两个数字,先放右边,再放左边,确保减和除的顺序不出错,算完后的结果再入栈,一直遍历下去直到字符串的末尾
具体代码
class Solution {
public int evalRPN(String[] tokens) {
//创建空栈
Stack<Integer> stack = new Stack<>();
//遍历数组
for(int i = 0; i < tokens.length; i++) {
String tmp = tokens[i];
//判断是数字还是符号
if(!isOperation(tmp)) {
//数字就入栈
Integer val = Integer.valueOf(tmp);
stack.push(val);
} else {
//符号就弹出两个数字
Integer val2 = stack.pop();
Integer val1 = stack.pop();
//用switch来选择要哪种运算
switch (tmp) {
//算完后结果再入栈
case "+":
stack.push(val1 + val2);
break;
case "-":
stack.push(val1 - val2);
break;
case "*":
stack.push(val1 * val2);
break;
case "/":
stack.push(val1 / val2);
break;
}
}
}
//遍历完字符串数组,弹出最终结果
return stack.pop();
}
public boolean isOperation(String s) {
if(s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")) {
return true;
}
return false;
}
}4. 队列的介绍和使用
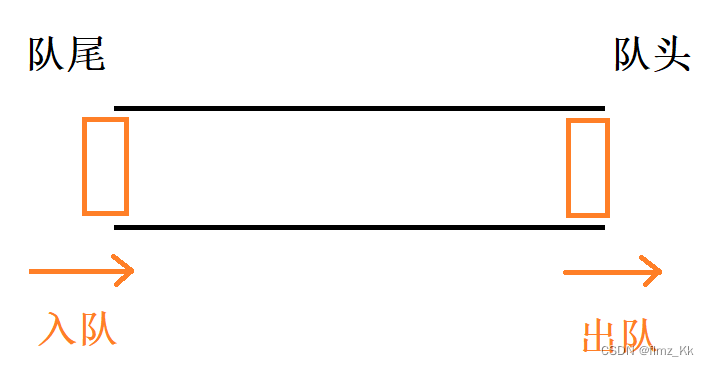
队列(Queue)也是一种特殊的线性表,他只允许在一端进行插入操作,在另一端进行删除操作,也就是先进先出。插入操作的一端就是队尾,删除操作的一端就叫做队头
入队:即数据从队尾入队
出队:即数据从队头出队
4.1 语法格式
(在Java中,Queue是一个接口,底层是用链表实现的,因此我们在实例化时必须用LinkedList的对象,因为LinkedList它实现了Queue接口)
import java.util.LinkedList;
import java.util.Queue;
Queue<Integer> queue = new LinkedList<>();
要记得导包
4.2 入队
boolean offer(E e):将e从队尾插入进队里,如果队列空间不够,则返回false
Queue<Integer> queue = new LinkedList<>();
queue.offer(12);
queue.offer(23);
queue.offer(34);
System.out.println(queue);运行结果如下
4.3 出队
E poll():将队头数据弹出,并返回该数据(会删除队头元素)E peek():获取队头数据,但并不删除
Queue<Integer> queue = new LinkedList<>();
queue.offer(12);
queue.offer(23);
queue.offer(34);
System.out.println(queue);
queue.poll();//删除12
Integer I = queue.peek();//获取队头元素
System.out.println(I);//23
System.out.println(queue);运行结果如下
4.4 队列的空间
(此处的方法均为Collection的方法,因为Queue没有判空等方法)
int size():获取队列的大小
boolean isEmpty():检测队列是否为空
Queue<Integer> queue = new LinkedList<>();
queue.offer(12);
queue.offer(23);
queue.offer(34);
System.out.println(queue);
System.out.println(queue.size());
System.out.println(queue.isEmpty());运行结果如下
5. 队列的模拟使用
5.1 链式存储结构
队列是一种特殊的顺序表,它始终遵循先进先出的原则。因此我们可以使用链表来模拟实现,即链式结构
public class MyQueue {
//创建链表
class ListNode {
public int val;
public ListNode prev;
public ListNode next;
public ListNode(int val) {
this.val = val;
}
}
public ListNode head;
public ListNode last;
//入队(尾插法)
public void offer(int val) {
ListNode node = new ListNode(val);
if (head == null) {
head = last = node;
} else {
last.next = node;
node.prev = last;
last = last.next;
}
}
//出队(头删法)返回出对的元素
public int poll() {
try {
checkQueueEmpty();
} catch (QueueEmptyException e) {
e.printStackTrace();
}
int ret = head.val;
if (head.next == null) {
head = last = null;
} else {
head = head.next;
head.prev = null;
}
return ret;
}
private void checkQueueEmpty() throws QueueEmptyException {
if (isEmpty()){
throw new QueueEmptyException("队列为空!");
}
}
//取出队头元素,不删除
public int peek() {
try {
checkQueueEmpty();
} catch (QueueEmptyException e) {
e.printStackTrace();
}
return head.val;
}
public boolean isEmpty() {
return head == null;
}
}栈的空间异常判断
public class QueueEmptyException extends RuntimeException{
public QueueEmptyException() {
}
public QueueEmptyException(String message) {
super(message);
}
}5.2 顺序存储结构
除了用链式结构,我们还可以使用顺序结构来模拟实现队列
public class MyQueue {
int[] array;
int front;
int rear;
public MyQueue(){
this.array = new int[10];
}
}初始状态(队列为空):front == rear == 0
进队:当队列不满时,先送数据到队尾,再将rear加1
出队:当队列不为空时,先把队头数据取出,再将front加1
但是当我们把队列内所有的元素都删除时,front又会等于rear,此时队列内为空,但front == rear ≠ 0,会出现“假溢出”现象
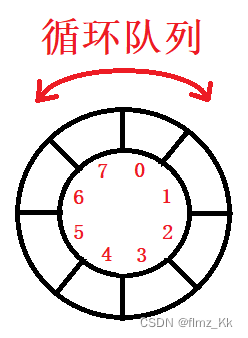
循环队列
为了解决“假溢出”现象,我们可以把队列头尾相接,形成循环队列。循环队列是一种头尾相接的顺序存储结构
当我们要向循环队列插入一个元素,此时如果last是在队尾,就应该:last = (last+1)%elem.length
当我们要把循环队列删除一个元素,此时如果first是在队头,就应该:first = (first+1)%elem.length
当我们想要区分队列是空是满,有三种方法:
1. 添加一个计数size,插入一个就size++,用size去跟array.length来比较判断
2. 浪费一个空间,这个空间不放元素,当last指向这里时,即为满
3. 使用标记,标记上队头队尾的位置,一旦first和last到那里,就能判断
可以做一下这道题加深理解 —— 力扣 622. 设计循环队列
6. 栈和队列的相互转换
6.1 用队列实现栈
原题地址: 力扣 225. 用队列实现栈
读题后我们可以提炼出重点:
- 我们可以使用两个队列,并且使用队列的标准操作(push、pop、peek、size、isEmpty)
- 我们要实现的是栈的四个基本操作:push、top、pop、empty(通过示例我们可以知道top等同于peek)
- 要注意MyStack类各方法的返回值
具体代码
1. 先把两个队列初始化:
public Queue<Integer> queue1;
public Queue<Integer> queue2;
public MyStack() {
queue1 = new LinkedList<>();
queue2 = new LinkedList<>();
}2. 判空 empty( ) :
public boolean empty() {
return (queue1.isEmpty() && queue2.isEmpty());
}3. 入栈 push( ):
入栈的思想很简单,哪个队列空了就放在哪个队列
我们可以先判断整个栈空不空,即使用empty,为true就直接放入队列1。不为空则表明俩队列有一个为空,一个不为空,照这个思路我们可以用代码来实现
public void push(int x) {
if (empty()) {
queue1.offer(x);
return;
}
if (!queue1.isEmpty()) {
queue1.offer(x);
} else {
queue2.offer(x);
}
}4. 出栈 pop( ):
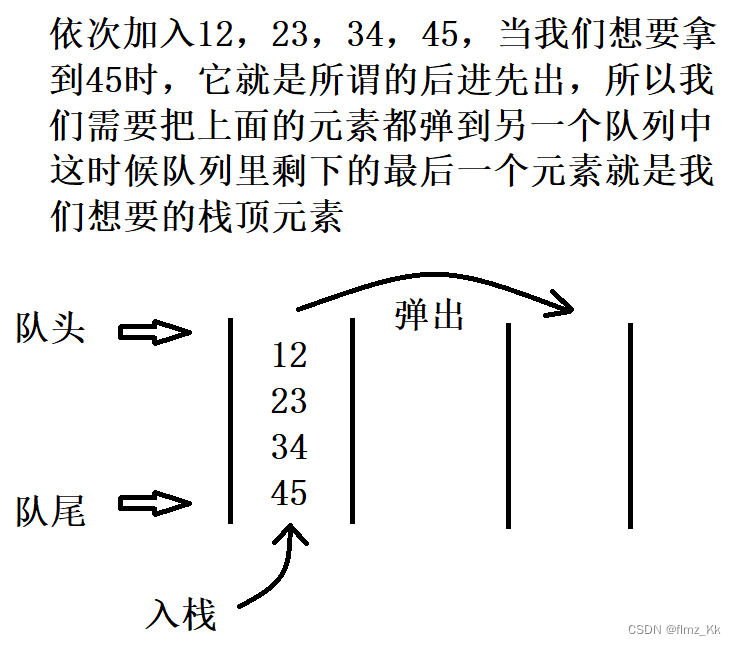
首先,判断栈是否为空,不为空直接返回-1(写个异常更好,此处不展示);接下来,把一个队列中的N-1个元素放到另一个队列中,此时队列剩下的最后一个元素就是我们要“出栈”的元素
public int pop() {
if (empty()) {
return -1;
}
if (!queue1.isEmpty()) {
int size = queue1.size();
for (int i = 0; i < size - 1; i++) {
queue2.offer(queue1.poll());
}
return queue1.poll();
} else {
int size = queue2.size();
for (int i = 0; i < size - 1; i++) {
queue1.offer(queue2.poll());
}
return queue2.poll();
}
}5. 获取栈顶元素 top( ):
思路跟出栈类似,但只是返回栈顶元素并不删除
public int top() {
if (empty()) {
return -1;
}
if (!queue1.isEmpty()) {
int size = queue1.size();
int ret = 0;
for (int i = 0; i < size; i++) {
ret = queue1.poll();
queue2.offer(ret);
}
return ret;
} else {
int size = queue2.size();
int ret = 0;
for (int i = 0; i < size; i++) {
ret = queue2.poll();
queue1.offer(ret);
}
return ret;
}
}6.2 用栈实现队列
原题地址:力扣 232. 用栈实现队列
同样我们先读题,提炼信息:
- 我们可以使用两个栈,并且使用队列的标准操作(push、pop、peek、size、isEmpty)
- 我们要实现的是栈的四个基本操作:push、pop、peek、empty
- 要注意MyQueue类各方法的返回值
具体代码
1. 先把两个栈初始化
Stack<Integer> stack1;
Stack<Integer> stack2;
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
2. 判空 empty( ):
public boolean empty() {
return stack1.empty() && stack2.empty();
}3. 入队 push( ):
直接把元素压入任一栈中
public void push(int x) {
stack1.push(x);
}4. 出队 pop( ):
队列的原则是先进先出,我们现在手头上有两个栈,当把第一个数据入栈时,此时要出队的就是它。所以我们可以用另一个栈来存放栈底之上的所有元素,最后元素即为要取出的元素。
因此我们得通过循环把栈1的元素全存到栈2里
public int pop() {
if (empty()) {
return -1;
}
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
return stack2.pop();
}5. 获取队头元素peek( ):
思路和出队类似,但我们不把元素弹出
public int peek() {
if (empty()) {
return -1;
}
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
return stack2.peek();
}结语
今天我们一起学习了栈和队列,它们俩在结构上和原则上都很类似,要牢记栈是先进后出,队列是先进先出,这些知识点在后面二叉树的学习中还会遇到,接下来博主会把链表的那篇博客补上,敬请期待吧
希望大家能喜欢这篇文章,有总结不到位的地方还请多多谅解,若有出现纰漏,希望大佬们看到错误之后能够在私信或评论区指正,博主会及时改正,共同进步!