[Collection与数据结构] PriorityQueue与堆

news2024/11/25 3:46:04

1. 优先级队列

1.1 概念

前面介绍过队列，队列是一种先进先出(FIFO)的数据结构，但有些情况下，操作的数据可能带有优先级，一般出队列时，可能需要优先级高的元素先出队列，该中场景下，使用队列显然不合适，比如：在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话.
在这种情况下，数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。
在这种情况下，数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。
在这里插入图片描述

2. 优先级队列的模拟实现

PriorityQueue底层实现使用了堆这种数据结构,堆实际上就是在完全二叉树的基础上做了一些调整,使得里面的元素按照一定地规则排列,而堆的元素存储在一个数组中.

2.1 堆的概念

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为 小堆(或大堆)。也就是任意拿出一棵子树来,子结点都比父结点小(或大).将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
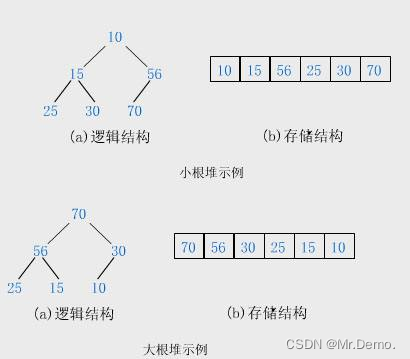
在这里插入图片描述

2.2 堆的性质

  • 堆是一颗完全二叉树
  • 堆中的某个结点的值总是不大于或者不小于父结点的值

2.3 堆的存储方式

从堆的概念可知，堆是一棵完全二叉树，因此可以层序的规则采用顺序的方式来高效存储.
实例如上图所示.
将元素存储到数组中后，可以根据二叉树章节的性质对树进行还原。假设i为节点在数组中的下标，则有：

  • 如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2
  • 如果2 * i + 1 小于节点个数(前提)，则节点i的左孩子下标为2 * i + 1，否则没有左孩子
  • 如果2 * i + 2 小于节点个数(前提)，则节点i的右孩子下标为2 * i + 2，否则没有右孩子

2.4 堆的创建

2.4.1 向下调整创建堆

对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据，如果将其创建成堆呢？
首先将数组中的元素按照二叉树层序遍历的方法进行存放.
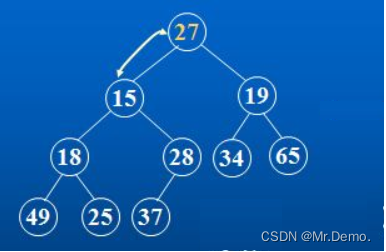
在这里插入图片描述
接下来,我们要做的就是对上面这颗二叉树进行向下调整.那么如何向下调整呢:我们以大根堆为例来说明.

  • 从堆的最后一棵子树开始比较父结点和子结点的大小关系.
  • 如果父结点的值小于两个子结点其中一个的值,则交换两个值,如果不是则停止向下调整.
  • 之后把父结点向上移动,再次向下调整,直到遇到父结点大于子结点或者调整到了根结点.
    下面画图来举例,我们给定一个任意完全二叉树:
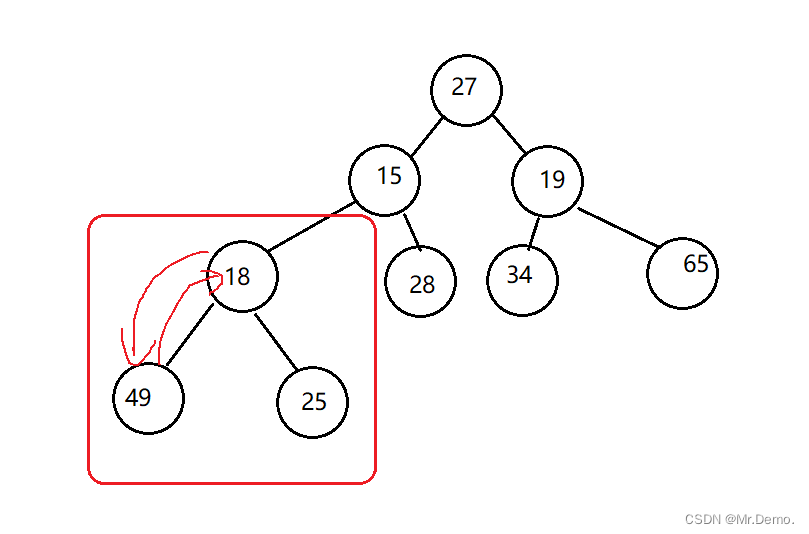
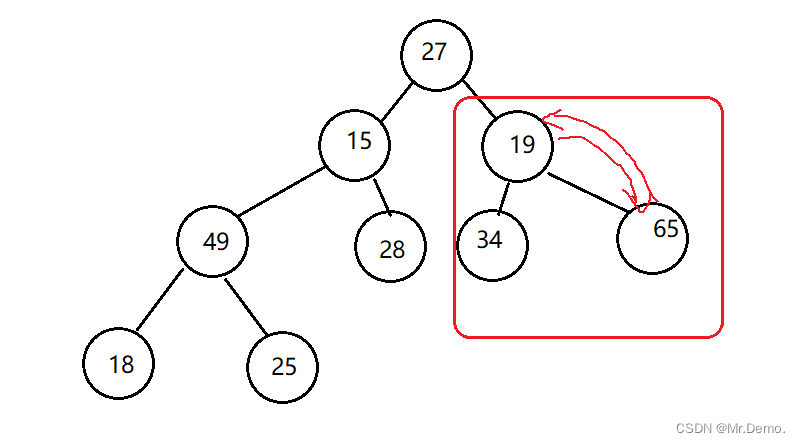
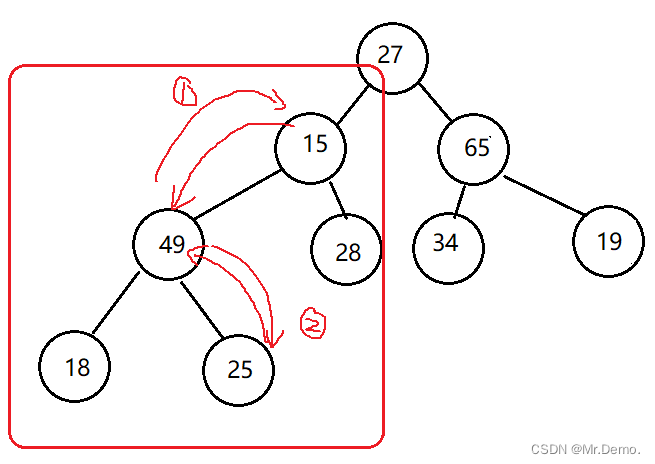
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    之后以此类推…
    为什么要从子树开始调整呢?因为首先要保证子树是大根堆,调整根层数更小的树的时候才会好调整.就像我们盖房子一样,先要把地基打牢,才可以盖得起高楼大厦.
    在这里插入图片描述
    接下来我们通过代码来创建一个大根堆:
public class MyPriorityQueue {
    public int usedSize;
    public int[] elem;//堆通过数组来实现

    public MyPriorityQueue(int[] elem) {
        this.elem = elem;
        usedSize += elem.length;
    }
    public void createBigHeap(){
        for (int parent = (usedSize-2)/2; parent >= 0 ; parent--) {//从最后一棵子树开始调整
            //之后根向上父结点向上走
            shiftDown(parent,usedSize-1);//向下调整
            //子结点永远是这棵树的最后一个结点
        }
    }

    /**
     * 向下调整
     * @param parent 父节点
     * @param end 结束位置
     */
    private void shiftDown(int parent,int end){
        int child = 2*parent+1;//此时child是左孩子
        while (child <= end){
            if (child+1 < usedSize && elem[child] < elem[child+1]){//若右孩子存在,并且大于左孩子
                child++;//让child到右孩子这里
            }
            if (elem[parent] < elem[child]){
                swap(parent,child);
                parent = child;
                child = 2*child+1;
            }else {
                break;//如果父结点不大于子结点,说明已经调整完成,因为是从下往上调的
            }
        }
    }
    private void swap(int s1,int s2){
        int tmp = elem[s1];
        elem[s1] = elem[s2];
        elem[s2] = tmp;
    }
}

2.4.1 创建堆的时间复杂度推导

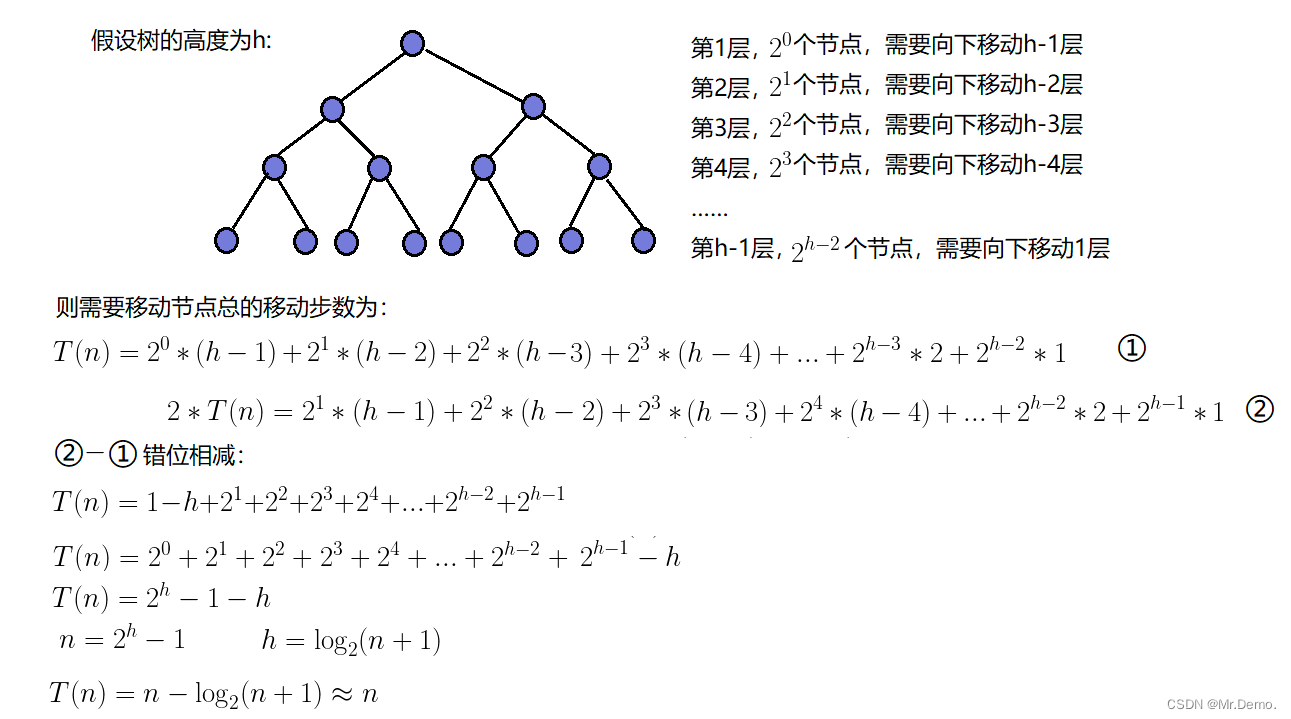
在这里插入图片描述
因此：建堆的时间复杂度为O(N).

2.5 堆的插入与删除

2.5.1 堆的插入

堆的插入分下面两个步骤:

  • 把结点插入树的最后一个位置
  • 把这个结点进行向上调整

那么,向上调整又如何调整呢?我们以大根堆为例

  • 把插入元素所在的结点与父节点进行比较.
  • 如果父结点小于插入结点,则交换两个结点,否则停止向上调整.
  • 如果成功交换,重复上述步骤,知道父结点大于子结点或者比较到根结点.
    下面我们通过代码来展示:
/**
     * 插入元素
     * @param val 要插入的值
     */
    public void offer(int val){
        if (isFull()){
            this.elem = Arrays.copyOf(elem,elem.length*2);
        }
        elem[usedSize] = val;
        usedSize++;
        shiftUp(usedSize-1);//这里注意是usedSize-1,因为usedSize++过,现在需要
        //向上调整的元素是usedSize-1位置上的元素
    }

    /**
     * 向上调整
     * @param child 因为向上调整的终点都是根结点,所以传入child
     */
    private void shiftUp(int child){
        int parent = (child - 1)/2;
        while (child > 0){
            if (elem[parent] < elem[child]){
                swap(elem[parent],elem[child]);
                child = parent;
                parent = (parent-1)/2;
            }else {
                break;
            }
        }
    }

    /**
     * 判断堆元素是否为满
     * @return
     */
    private boolean isFull(){
        if (elem.length == usedSize){
            return true;
        }else {
            return false;
        }
    }

2.5.2 堆的删除

注意:在删除元素的时候,一定删除的是堆顶元素.

  • 将堆顶元素和最后一个元素进行交换
  • 删除最后一个元素
  • 将堆顶结点进行向下调整
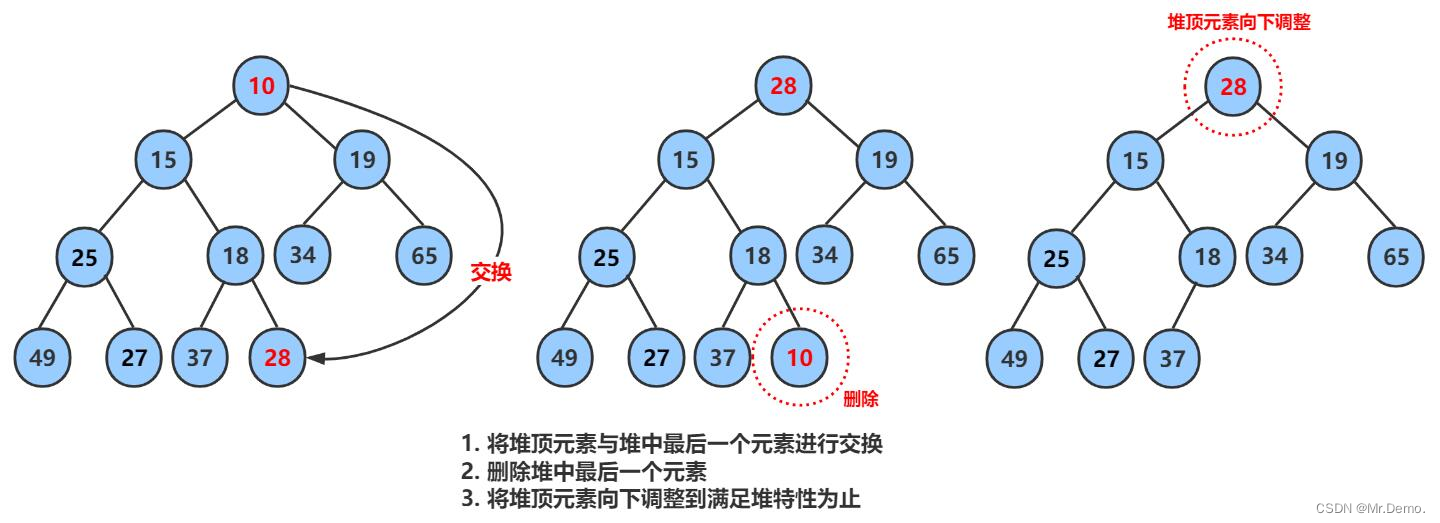
    在这里插入图片描述
    下面通过代码来展示:
/**
     * 删除堆顶元素
     */
    public void poll(){
        if (usedSize == 0){
            return;
        }
        swap(elem[0],elem[usedSize-1]);
        usedSize --;
        shiftDown(0,usedSize-1);
    }

3. PriorityQueue

3.1 PriorityQueue的性质

Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的，本文主要介绍PriorityQueue.
关于PriorityQueue的使用要注意：

  1. 使用时必须导入PriorityQueue所在的包，即：
    import java.util.PriorityQueue;
  2. PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出ClassCastException异常
  3. 不能插入null对象，否则会抛出NullPointerException
  4. 没有容量限制，可以插入任意多个元素，其内部可以自动扩容
  5. 插入和删除元素的时间复杂度为O(log2N)
  6. PriorityQueue底层使用了堆数据结构
  7. PriorityQueue默认情况下是小堆—即每次获取到的元素都是最小的元素.要想创建大根堆,必须传入比较器对象.

3.2 PriorityQueue的使用

  1. 构造方法
构造器功能介绍
PriorityQueue()创建一个空的优先级队列，默认容量是11
PriorityQueue(int initialCapacity)创建一个初始容量为initialCapacity的优先级队列，注意:initialCapacity不能小于1，否则会抛IllegalArgumentException异常
PriorityQueue(Collection<? extends E> c)用一个集合来创建优先级队列
public PriorityQueue(Comparator<? super E> comparator)传入比较器----改变元素之间的比较规则

源码如下:

private static final int DEFAULT_INITIAL_CAPACITY = 11;//默认容量
public PriorityQueue() {
       this(DEFAULT_INITIAL_CAPACITY, null);
   }
public PriorityQueue(int initialCapacity) {//用户传入自定义容量
        this(initialCapacity, null);
    }
public PriorityQueue(Comparator<? super E> comparator) {
        this(DEFAULT_INITIAL_CAPACITY, comparator);//通过比较器改变优先级队列中元素的比较规则
    }
public PriorityQueue(Collection<? extends E> c) {
        if (c instanceof SortedSet<?>) {
            SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
            this.comparator = (Comparator<? super E>) ss.comparator();
            initElementsFromCollection(ss);
        }
        else if (c instanceof PriorityQueue<?>) {
            PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;
            this.comparator = (Comparator<? super E>) pq.comparator();
            initFromPriorityQueue(pq);
        }
        else {
            this.comparator = null;
            initFromCollection(c);
        }
    }

使用实例:

static void TestPriorityQueue(){
        // 创建一个空的优先级队列，底层默认容量是11
        PriorityQueue<Integer> q1 = new PriorityQueue<>();
 
        // 创建一个空的优先级队列，底层的容量为initialCapacity
        PriorityQueue<Integer> q2 = new PriorityQueue<>(100);
 
        ArrayList<Integer> list = new ArrayList<>();
        list.add(4);
        list.add(3);
        list.add(2);
        list.add(1);
 
        // 用ArrayList对象来构造一个优先级队列的对象
        // q3中已经包含了三个元素
        PriorityQueue<Integer> q3 = new PriorityQueue<>(list);
        System.out.println(q3.size());
        System.out.println(q3.peek());
   }

通过传入比较器来创建大根堆:

public class Compare implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2-o1;
    }
}
public class Main {
    public static void main(String[] args) {
        PriorityQueue<Integer> priorityQueue1 = new PriorityQueue<>(new Compare());
        priorityQueue1.offer(1);
        priorityQueue1.offer(2);
        priorityQueue1.offer(3);
        priorityQueue1.offer(4);
        priorityQueue1.offer(5);
        System.out.println(priorityQueue1);//通过传入比较器对象,可以构建大根堆
    }
}

也可以通过传入比较器使得不可比较的对象变为可比较的对象:

public class Student{
    public String name;
    public int age;

    @Override
    public String toString() {
        return "Student{" +
                "name='" + name + '\'' +
                ", age=" + age +
                '}';
    }

    public Student(String name, int age) {
        this.name = name;
        this.age = age;
    }
}
import java.util.Comparator;

/**
 * 年龄比较规则
 */
public class Compare1 implements Comparator<Student> {
    @Override
    public int compare(Student o1, Student o2) {
        return o2.age - o1.age;
    }
}
public class Main {
    public static void main(String[] args) {
        PriorityQueue<Student> priorityQueue2 = new PriorityQueue<>(new Compare1());
        //由于Student没有默认创建比较方法,所以必须传入比较器对象,否者异常
        priorityQueue2.offer(new Student("zhangsan",12));
        priorityQueue2.offer(new Student("lisi",17));
        priorityQueue2.offer(new Student("wangwu",19));
        System.out.println(priorityQueue2);//按照年龄进行大根堆构建
    }
}

也可以不传入比较器,在类中重写Comparable接口的compareTo方法:

public class Student implements Comparable<Student>{
    public String name;
    public int age;

    @Override
    public String toString() {
        return "Student{" +
                "name='" + name + '\'' +
                ", age=" + age +
                '}';
    }

    public Student(String name, int age) {
        this.name = name;
        this.age = age;
    }

    @Override
    public int compareTo(Student o) {
        return this.name.compareTo(o.name);
    }
}
public class Main {
    public static void main(String[] args) {
        PriorityQueue<Student> priorityQueue3 = new PriorityQueue<>();
        priorityQueue3.offer(new Student("zhang",12));
        priorityQueue3.offer(new Student("li",15));
        priorityQueue3.offer(new Student("wang",17));
        System.out.println(priorityQueue3);
    }
}
  1. 插入,删除,获取优先级队列中的方法
函数名功能介绍
boolean offer(E e)插入元素e，插入成功返回true，如果e对象为空，抛出NullPointerException异常，时间复杂度 ，注意：空间不够时候会进行扩容
E peek()获取优先级最高的元素，如果优先级队列为空，返回null
E poll()移除优先级最高的元素并返回，如果优先级队列为空，返回null
int size()获取有效元素的个数
void clear()清空
boolean isEmpty()检测优先级队列是否为空，空返回true
  1. 优先级队列的扩容
    jdk17 的源码如下:
public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1);//大于队列大小的时候,进行扩容
        siftUp(i, e);
        size = i + 1;
        return true;
    }
private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        // Double size if small; else grow by 50%
        int newCapacity = ArraysSupport.newLength(oldCapacity,
                minCapacity - oldCapacity, /* minimum growth */
                oldCapacity < 64 ? oldCapacity + 2 : oldCapacity >> 1
                                           /* preferred growth */);
        queue = Arrays.copyOf(queue, newCapacity);
    }

优先级队列的扩容说明：

  • 容量小于64的时候,按照2倍扩容.
  • 容量大于64的时候,按照1.5倍扩容.

4. top-k问题

这种算法一般适用于数据比较大的情况下,比如要在1亿,甚至10亿数据中找出前k的数据.
OJ链接
在这里插入图片描述

class BigComparator implements Comparator<Integer> {

    @Override
    public int compare(Integer o1, Integer o2) {
        return o2-o1;//通过比较器来创建大根堆
    }
}
public class Top_k {
    public int[] smallestK(int[] arr, int k) {
        if (k <= 0){;
            return new int[0];//如果k==0,返回空数组
        }
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new BigComparator());
        //先取前k个元素放入
        for (int i = 0; i < k; i++) {
            priorityQueue.offer(arr[i]);
        }
        //如果堆顶元素大于遍历到的元素,删除堆顶元素,让遍历到的元素进来
        for (int i = k; i < arr.length; i++) {
            if (priorityQueue.peek() > arr[i]){
                priorityQueue.poll();
                priorityQueue.offer(arr[i]);
            }
        }
        int[] array = new int[k];
        //使用数组取出前k个元素
        for (int i = 0; i < k; i++) {
            array[i] = priorityQueue.poll();
        }
        return array;
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1617741.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

持续更新。。。

持续更新。。。

1、JAVA面试指南 https://javaguide.cn/ 简历优化&#xff1a;突出与应聘职位相关的项目经验、技术栈、技能证书和专业成就。确保简历中的技术关键词与JD&#xff08;Job Description&#xff09;相符。 自我评估&#xff1a;对照目标职位要求&#xff0c;梳理自身Java技能树&…
阅读更多...
mac安装nvm管理node(手残流，git下载)

mac安装nvm管理node(手残流，git下载)

1. 准备 首先电脑里得有brew、git、vscode&#xff0c;看这里安装brew、git&#xff0c;看这里安装vscode。 我本人比较low&#xff0c;mac命令也记不熟&#xff0c;本篇就是git下载nvm&#xff0c;vscode看配置&#xff0c;省心不动脑子就可以了。 2. 清理node 如果mac里没…
阅读更多...
Xshell正版免费使用（学生党）

Xshell正版免费使用（学生党）

话不多说&#xff0c;上链接 https://www.xshell.com/zh/free-for-home-school/
阅读更多...
Introducing Meta Llama 3: The most capable openly available LLM to date

Introducing Meta Llama 3: The most capable openly available LLM to date

要点 今天&#xff0c;我们推出 Meta Llama 3&#xff0c;这是我们最先进的开源大型语言模型的下一代。Llama 3型号将很快在AWS&#xff0c;Databricks&#xff0c;Google Cloud&#xff0c;Hugging Face&#xff0c;Kaggle&#xff0c;IBM WatsonX&#xff0c;Microsoft Azur…
阅读更多...
Linux学习：文件描述符fd

Linux学习：文件描述符fd

目录 1. 引子2. C语言文件接口2.1 文件的打开与关闭的操作2.2 文件写入读取操作2.3 当前路径 3. 文件I/O操作与系统调用3.1 程序默认打开的文件流3.2 操作系统访问文件的系统调用接口3.2.1 文件打开与关闭操作3.2.2 写入与读取操作 4. 什么是文件描述符fd4.1 进程与文件的关系4…
阅读更多...
【笔记】Telephony SIM SPN及运营商名称显示数据来源介绍

【笔记】Telephony SIM SPN及运营商名称显示数据来源介绍

来源介绍 网络名称显示 来源及优先级&#xff08;高到低&#xff09; SourceCommentEnhanced Operator Name String(Eons) 名称信息存放&#xff1a; EF_PNN(PLMN Network Name, fid: 6FC5) &#xff1a;LAC和EF_PNN中的Record Identifier EF_OPL(Operator PLMN List, fid: 6FC…
阅读更多...
RBA认证是什么？RBA认证的流程是怎么样的

RBA认证是什么？RBA认证的流程是怎么样的

RBA认证&#xff0c;即“责任商业联盟”认证&#xff0c;英文全称是Responsible Business Alliance。这是一个为电子行业或以电子为主要组成部分的行业及其供应链制定的社会责任审核标准。该标准旨在确保工作环境的安全、工人受到尊重并富有尊严、商业营运合乎环保性质并遵守道…
阅读更多...
【AI】如何让局域网PC能够访问langchain框架的AI服务

【AI】如何让局域网PC能够访问langchain框架的AI服务

【背景】 在单位内部成功运行了langchain服务&#xff0c;但是发现本地可以用默认8000端口访问&#xff0c;但是局域网内其它机器却无法访问服务页面。 【分析】 首先查看项目文件夹中的server.py。由于这个server.py的存在&#xff0c;我一开始以为langchain整套框架的服务…
阅读更多...
哪些因素影响了PCB电路板切割精度？

哪些因素影响了PCB电路板切割精度？

PCB电路板切割是电子制造过程中一个至关重要的环节&#xff0c;其精度对后续工序的质量和效率具有决定性影响。因此&#xff0c;了解影响PCB电路板切割精度的原因&#xff0c;对于提高电子产品的质量和生产效率具有重要意义。 1. PCB分板机稳定性 PCB分板机的性能直接影响到切…
阅读更多...
中国AIGC最值得关注企业产品榜单揭晓！首份应用全景图谱发布

中国AIGC最值得关注企业产品榜单揭晓！首份应用全景图谱发布

组委会 发自 凹非寺 量子位 | 公众号 QbitAI “你好&#xff0c;新应用&#xff01;” 站在大模型落地元年&#xff0c;是时候喊出这句话了。 从软件APP、智能终端乃至具身智能等等&#xff0c;AIGC开始席卷一切。 大模型玩家、互联网巨头、终端厂商、垂直场景玩家纷纷入场…
阅读更多...
web测试基础知识

web测试基础知识

目录 web系统的基础 web概念(worldwideweb) 网络结构 发展 架构 B/S C/S P2P 工作原理 静态页面 动态页面 web客户端技术 浏览器的核心--渲染引擎 web服务器端技术 web服务器 应用服务器 集群环境 数据库 案例-URL 协议类型 主机名 端口 IP地址 分类 …
阅读更多...
Ubuntu 安装 Harbor

Ubuntu 安装 Harbor

一、安装 docker 原文参考传送门 1st 卸载系统自带的 docker 应用 for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done 2nd 设置Docker 的apt源 # Add Dockers official GPG key: sudo…
阅读更多...
翻译《The Old New Thing》 - Some reasons not to do anything scary in your DllMain

翻译《The Old New Thing》 - Some reasons not to do anything scary in your DllMain

Some reasons not to do anything scary in your DllMain - The Old New Thing (microsoft.com)https://devblogs.microsoft.com/oldnewthing/20040127-00/?p40873 Raymond Chen 2004年01月27日 简介 这篇文章讨论了为什么不应该在DLL的DllMain函数中执行复杂的操作 正文 众所…
阅读更多...
SAP DMS创建文档根目录操作简介

SAP DMS创建文档根目录操作简介

前面我们已经对DMS的后台进行了系统的配置，本文开始我们对DMS的前台操作进行说明 1、CV01N创建文档 注意：EDIPUBLICROOTFOLDER为根目录的凭证号，不允许更改。 输入好后回车。进入下图所示： 点击文档浏览器，进入下一屏如下图： 注意：点击创建新的私人文件夹按创建是创…
阅读更多...
使用CSS3 + Vue3 + js-tool-big-box工具，实现炫酷五一倒计时动效

使用CSS3 + Vue3 + js-tool-big-box工具，实现炫酷五一倒计时动效

时间过得真是飞速&#xff0c;很快又要到一年一度的五一劳动节啦&#xff0c;今年五天假&#xff0c;做好准备了吗&#xff1f;今天我们用CSS3 Vue3 一个前端工具库 js-tool-big-box来实现一个炫酷的五一倒计时动效吧。 目录 1 先制作一个CSS3样式 2 Vue3功能提前准备 3…
阅读更多...
基于DEAP数据集的四种机器学习方法的情绪分类

基于DEAP数据集的四种机器学习方法的情绪分类

在机器学习领域&#xff0c;KNN&#xff08;K-Nearest Neighbors&#xff09;、SVM&#xff08;Support Vector Machine&#xff09;、决策树&#xff08;Decision Tree&#xff09;和随机森林&#xff08;Random Forest&#xff09;是常见且广泛应用的算法。 介绍 1. KNN&am…
阅读更多...
windows本地提权--令牌窃取烂土豆UAC

windows本地提权--令牌窃取烂土豆UAC

免责声明:本文仅做技术交流与学习,请知法守法,不要乱搞破坏等等... 目录 一.令牌窃取 操作: 1-生成-->上传后门后,让msf上线 2-执行命令 二.烂土豆(MS16-075) 操作: 1-先让MSF上线 2-上传烂土豆 3-执行命令 三.UAC(用户账户控制) 1-MSF模块提权 2-UACME 项目(yy…
阅读更多...
Kafak详解（1）

Kafak详解（1）

简介 消息队列 为什么要有消息队列 图-1 消息队列的使用 消息队列 1)消息Message&#xff1a;网络中的两台计算机或者两个通讯设备之间传递的数据。例如说&#xff1a;文本、音乐、视频等内容。 2)队列Queue&#xff1a;一种特殊的线性表(数据元素首尾相接)&#xff0c;特…
阅读更多...
应对电网挑战！lonQ与橡树岭国家实验室利用量子技术改善关键基础设施

应对电网挑战！lonQ与橡树岭国家实验室利用量子技术改善关键基础设施

内容来源&#xff1a;量子前哨&#xff08;ID&#xff1a;Qforepost&#xff09; 文丨浪味仙 排版丨沛贤 深度好文&#xff1a;1800字丨6分钟阅读 摘要&#xff1a;美国电网正在面临需求增加和能源扩散的挑战&#xff0c;对能够应对优化和安全挑战的创新解决方案有着迫切需求…
阅读更多...
黑马鸿蒙学习5：LIST容器

黑马鸿蒙学习5：LIST容器

LIST容器&#xff0c;其实就是如果FOREACH容器展示不全的话&#xff0c;会自动有滚动条了。要注意的是&#xff0c;LIST中必须有固定的listitem这个项&#xff0c;而且列表里面只能包含一个根组件。 必须把ROW容器放到listitem中&#xff0c;如下&#xff1a;
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023