算法——BFS算法

news2024/9/22 15:37:09

1. 什么是BFS算法

BFS（广度优先搜索，Breadth-First Search）算法是一种用于图和树等数据结构中进行搜索的基本算法。它从指定的起始节点开始，逐层地向外扩展搜索，直到找到目标节点或遍历完整个图。

BFS算法的基本思想是：先访问起始节点，然后依次访问起始节点的邻居节点，再依次访问邻居节点的邻居节点，以此类推，直到搜索到目标节点或者遍历完整个图。BFS算法使用队列来辅助实现节点的遍历顺序，保证每一层的节点按顺序访问。

2. 应用实例

①BFS解决FloodFill问题

1. 图像渲染

题目链接：733. 图像渲染 - 力扣（LeetCode）

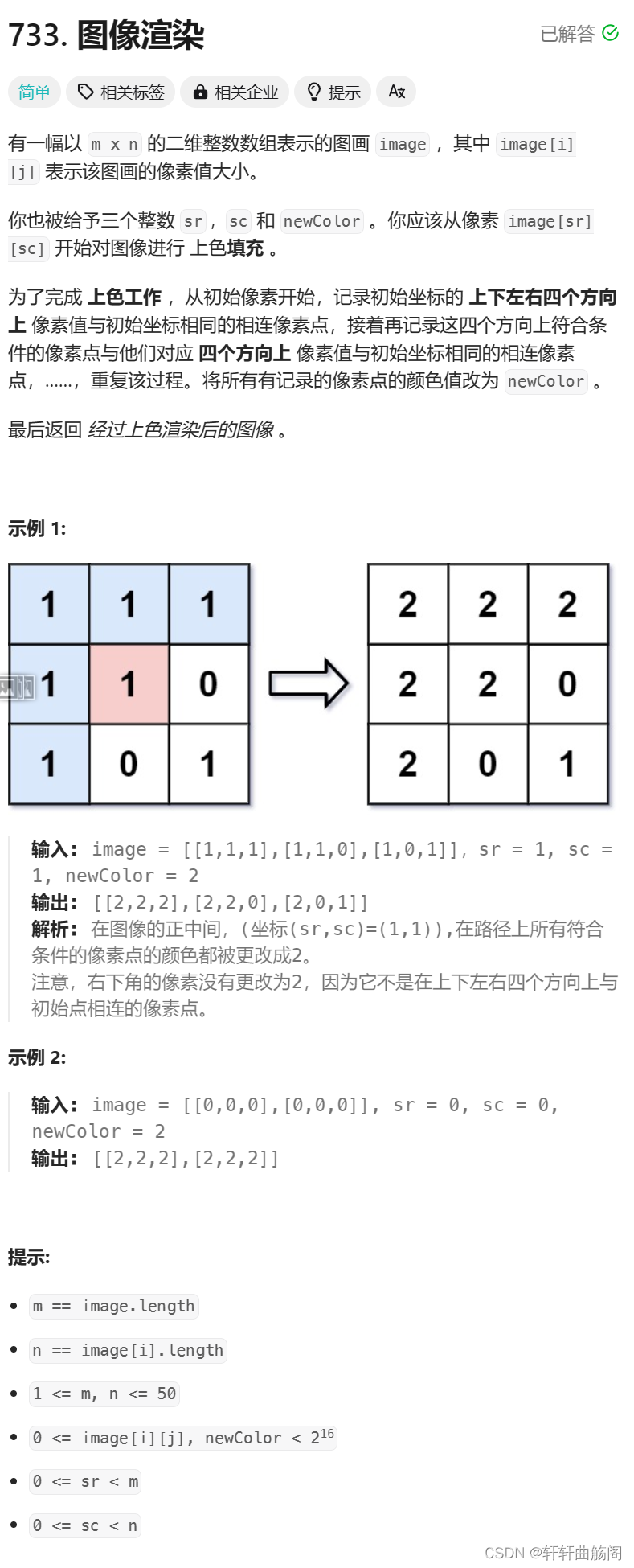
解析：题目的要求是对一大批性质相同的连续区域进行处理，我们可以使用BFS来进行处理，代码如下

class Solution 
{
public:
    int dx[4] = {1,-1,0,0};
    int dy[4] = {0,0,1,-1};
    int m,n;
    int check[51][51] = {0};

    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) 
    {
        m = image.size(), n = image[0].size();
        queue<pair<int, int>> q;
        q.push({sr,sc});

        while (!q.empty())
        {
            int sz = q.size();
            while (sz--)
            {
                auto pair = q.front();
                int a = pair.first, b = pair.second;
                int prevcolor = image[a][b];
                image[a][b] = color;
                q.pop();
                for (int i = 0; i < 4; i++)
                {
                    int x = a + dx[i], y = b + dy[i];
                    if (x >= 0 && x < m && y >= 0 && y < n && image[x][y] == prevcolor && !check[x][y])
                    {
                        q.push({x, y});
                        check[x][y] = 1;
                    }
                }
            }
        }

        return image;
    }
};

2. 岛屿数量

题目链接：200. 岛屿数量 - 力扣（LeetCode）

解析：根据题目要求，我们在每次遇见‘1’时，从这个位置开始进行一次bfs将所有相邻为‘1’的区域置为‘0’，在每次进入后记录一次岛屿个数，遍历一遍之后就能得到答案，代码如下

class Solution 
{
public:
    int dx[4] = {0,0,1,-1};
    int dy[4] = {1,-1,0,0};
    int m,n;
    int check[301][301] = {0};

    void bfs(vector<vector<char>>& grid, int row, int col)
    {
        queue<pair<int, int>> q;
        q.push({row, col});

        while (!q.empty())
        {
            int sz = q.size();
            while (sz--)
            {
                auto [a, b] = q.front();
                q.pop();
                grid[a][b] = '0';
                for (int i = 0; i < 4; i++)
                {
                    int x = a + dx[i], y = b + dy[i];
                    if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == '1' && !check[x][y])
                    {
                        q.push({x, y});
                        check[x][y] = 1;
                    } 
                }
            }
        }
    }

    int numIslands(vector<vector<char>>& grid) 
    {
        int count = 0;
        m = grid.size(), n = grid[0].size();
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                if (grid[i][j] == '1') 
                {
                    bfs(grid, i, j);
                    count++;
                }

        return count;
    }
};

3. 岛屿的最大面积

题目链接：695. 岛屿的最大面积 - 力扣（LeetCode）

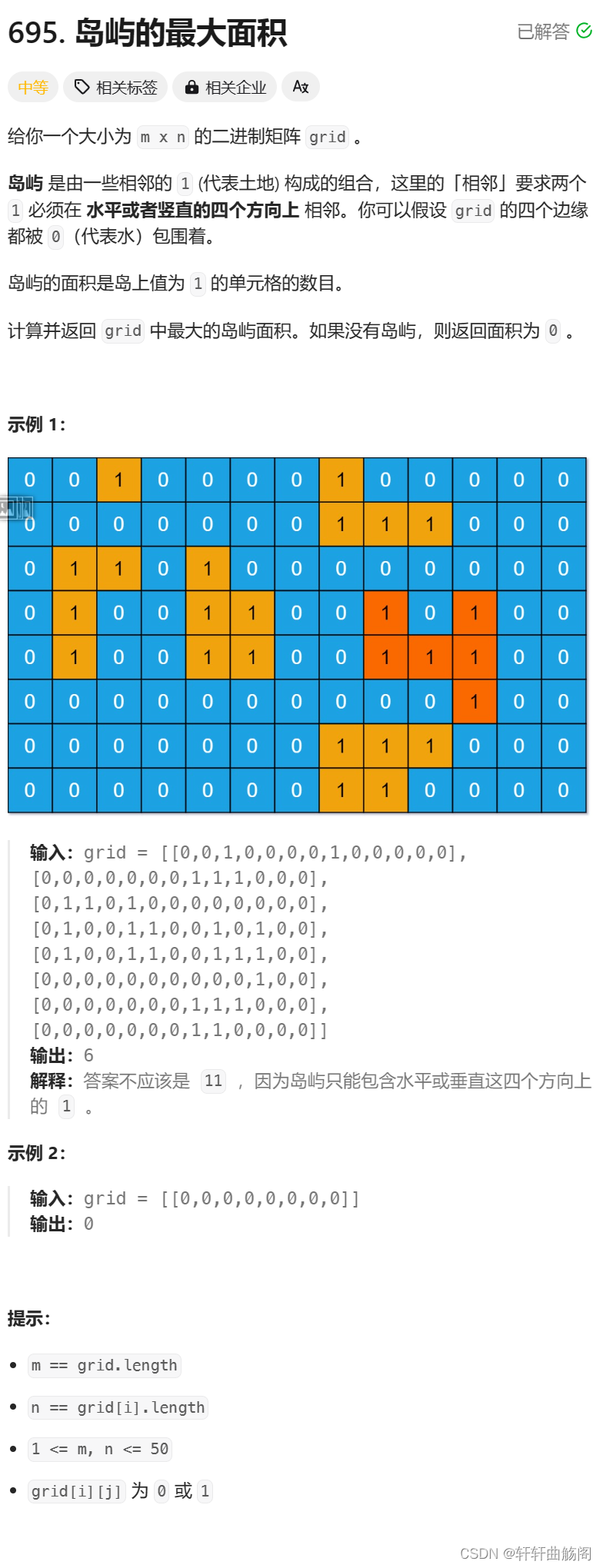
解析：我们可以在遇见值为1的区域时，我们对其使用一次bfs统计该区域岛屿大小，边统计边将其置为0，最后与ret相比较，让ret更新为最大值并返回，代码如下

class Solution 
{
public:
    int m, n, ret;
    int dx[4] = {1,-1,0,0};
    int dy[4] = {0,0,1,-1};
    int check[51][51] = {0};

    void bfs(vector<vector<int>>& grid, int row, int col)
    {
        int area = 0;
        queue<pair<int, int>> q;
        q.push({row, col});

        while (!q.empty())
        {
            int sz = q.size();
            while (sz--)
            {
                auto [a, b] = q.front();
                area++;
                q.pop();
                grid[a][b] = 0;
                for (int i = 0; i < 4; i++)
                {
                    int x = a + dx[i], y = b + dy[i];
                    if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !check[x][y])
                    {
                        q.push({x, y});
                        check[x][y] = 1;
                    }
                }
            }
        }

        ret = max(ret, area);
    }

    int maxAreaOfIsland(vector<vector<int>>& grid) 
    {
        ret = 0;
        m = grid.size(), n = grid[0].size();
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                if (grid[i][j] == 1) bfs(grid, i, j);

        return ret;
    }
};

4. 被围绕的区域

题目链接：130. 被围绕的区域 - 力扣（LeetCode）

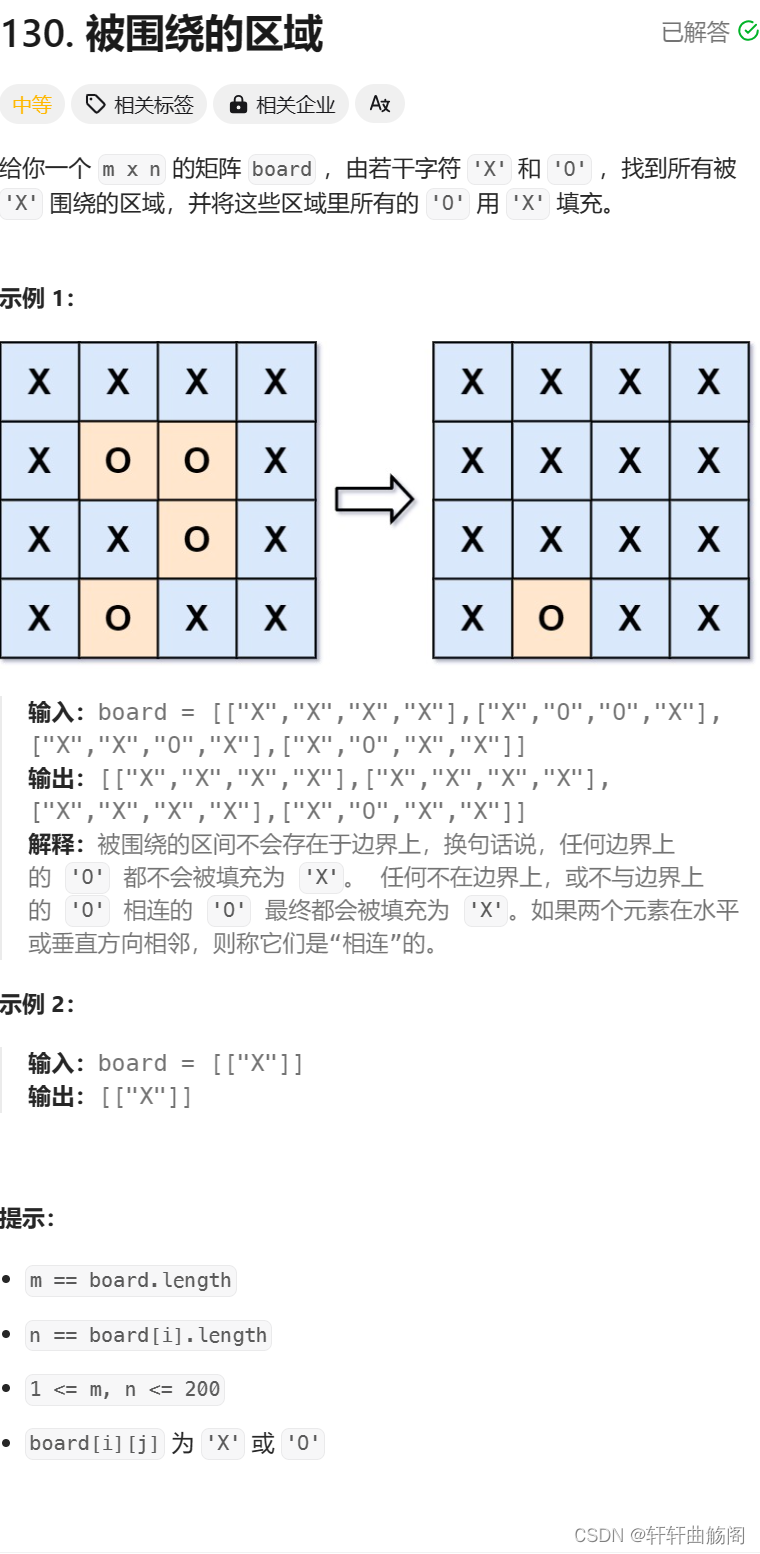
解析：分析题意，我们可以先遍历图形的四周，遇见'O'就进行一次bfs，将所有与边缘相连的'O'均设置为'A'（随意），然后遍历整个图形，将为‘O’的改为‘X’，为‘A’的改为‘O’即可，代码如下

class Solution 
{
public:
    int m,n;
    int dx[4] = {1,-1,0,0};
    int dy[4] = {0,0,1,-1};
    int check[201][201] = {0};

    void bfs(vector<vector<char>>& board, int row, int col, char flag)
    {
        queue<pair<int, int>> q;
        q.push({row, col});

        while (!q.empty())
        {
            int sz = q.size();
            while (sz--)
            {
                auto [a, b] = q.front();
                q.pop();
                check[a][b] = 1;
                board[a][b] = flag;
                for (int i = 0; i < 4; i++)
                {
                    int x = a + dx[i], y = b + dy[i];
                    if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O' && !check[x][y])
                    {
                        q.push({x, y});
                        check[x][y] = 1;
                    }
                }
            }
        }
    }

    void solve(vector<vector<char>>& board) 
    {
        m = board.size(), n = board[0].size();
        for (int i = 0; i < m; i++) 
        {
            if (board[i][0] == 'O') bfs(board, i, 0, 'A');
            if (board[i][n-1] == 'O') bfs(board, i, n-1, 'A');
        }
        for (int j = 0; j < n; j++) 
        {
            if (board[0][j] == 'O') bfs(board, 0, j, 'A');
            if (board[m-1][j] == 'O') bfs(board, m-1, j, 'A');
        }

        for (auto& v : board)
            for (auto& ch : v) 
                if (ch == 'O') ch = 'X';
                else if (ch == 'A') ch = 'O';
    }
};